人教版八年级下册19章一次函数的图像和性质 章节总复习课件(35张PPT)
文档属性
| 名称 | 人教版八年级下册19章一次函数的图像和性质 章节总复习课件(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览






文档简介
一次函数的图象与性质
章节总复习
注意:
请同学们先准备好笔和草稿纸。
在需要笔记时候截图,在需要思考时候点暂停视频,解答出来后再点继续观看。
考点1 一次函数与正比例函数的概念
一次
函数
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数
正比例函数
特别地,当b=0时,一次函数y=kx+b变为y=kx(k为常数,k≠0),这时y叫做x的正比例函数(特殊的一次函数)
考点小结
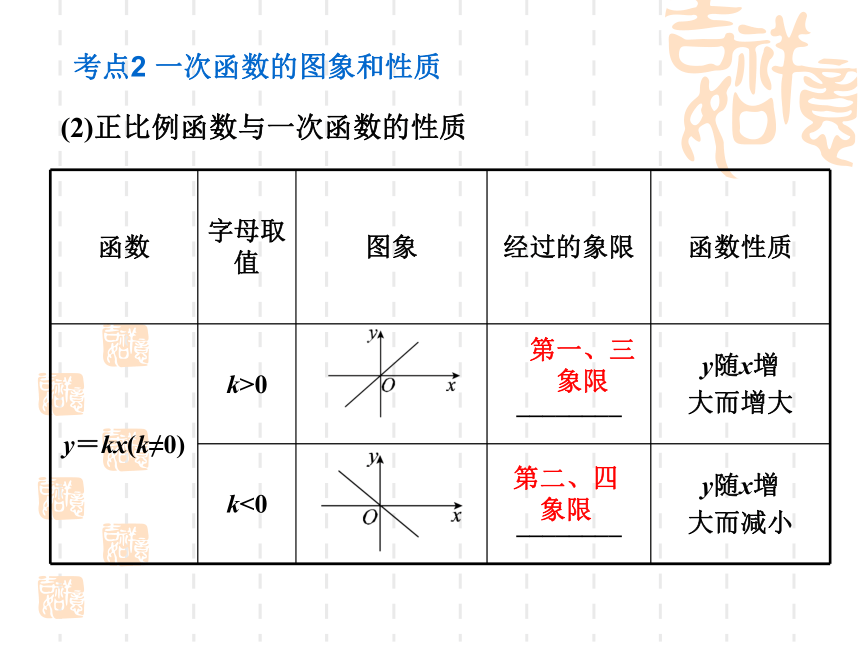
(2)正比例函数与一次函数的性质
函数
字母取值
图象
经过的象限
函数性质
y=kx(k≠0)
k>0
________
y随x增
大而增大
k<0
________
y随x增
大而减小
第一、三
象限
第二、四
象限
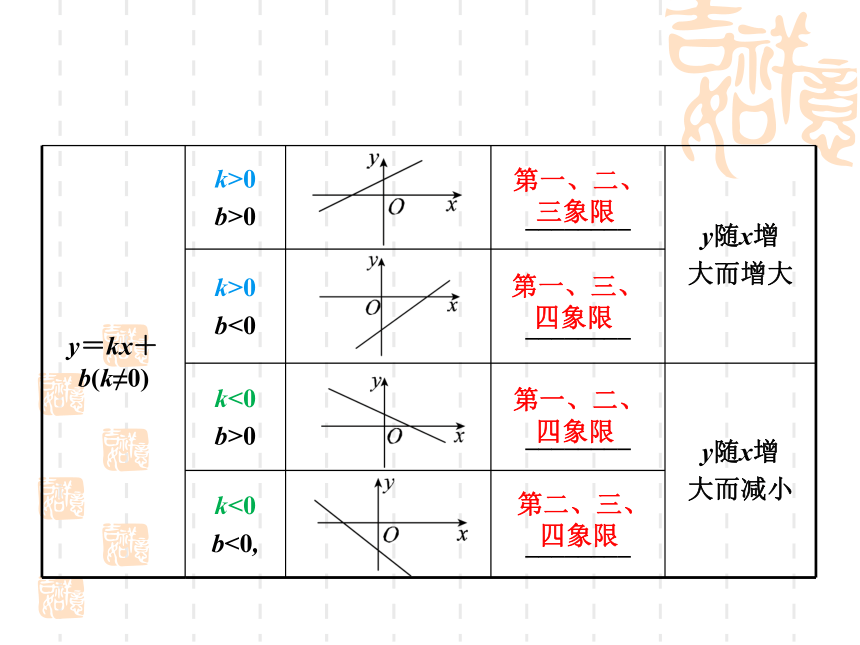
考点2 一次函数的图象和性质
y=kx+b(k≠0)
k>0
b>0
________
y随x增
大而增大
k>0
b<0
________
k<0
b>0
________
y随x增
大而减小
k<0
b<0,
________
第一、二、
三象限
第一、三、
四象限
第一、二、
四象限
第二、三、
四象限
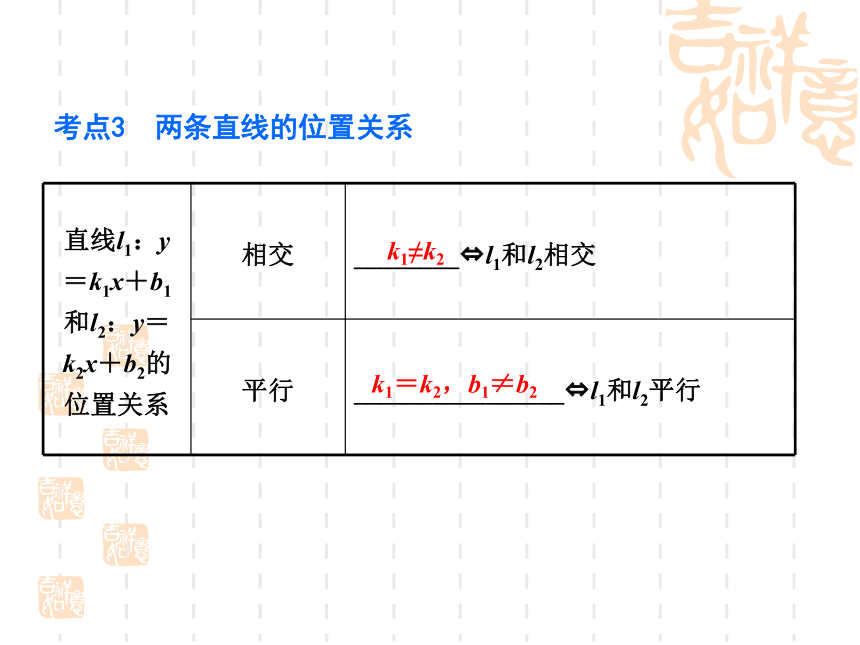
考点3 两条直线的位置关系
直线l1:y=k1x+b1和l2:y=k2x+b2的位置关系
相交
________?l1和l2相交
平行
________________?l1和l2平行
k1≠k2
k1=k2,b1≠b2
考点4 两直线的交点坐标及一次函数的图象与坐标
轴围成的三角形的面积
一条直线与坐标轴围成的三角形的面积
解由两个函数解析式组成的二元方程组,方程组的解即两函数图象的交点坐标
一条直线与其他一次函数图象的交点坐标
设x=0,求出对应的y值
一条直线与y轴的交点坐标
设y=0,求出对应的x值
一条直线与x轴的交点坐标
求法
分类
考点5 由待定系数法求一次函数的解析式
待定系数法
考点6 一次函数与一次方程(组)、一元一次不等式(组)
0
>
<
直线和其中一点的关系
直线和其中一段的关系
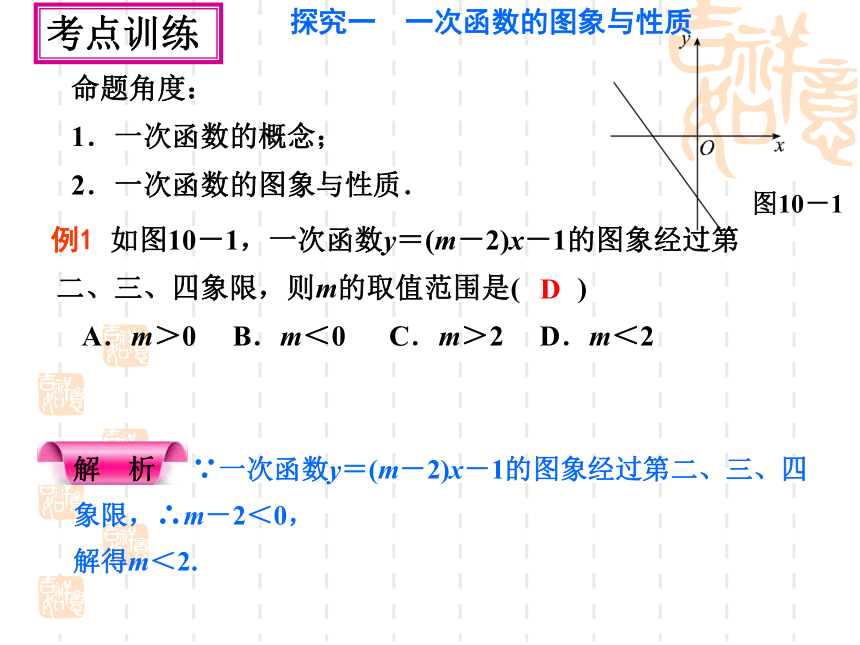
探究一 一次函数的图象与性质
命题角度:
1.一次函数的概念;
2.一次函数的图象与性质.
例1
如图10-1,一次函数y=(m-2)x-1的图象经过第二、三、四象限,则m的取值范围是( )
A.m>0 B.m<0 C.m>2 D.m<2
D
图10-1
解 析 ∵一次函数y=(m-2)x-1的图象经过第二、三、四象限,∴m-2<0,
解得m<2.
考点训练
2、 一次函数y=(m+2)x+1,若y随x的增大而减小,则m的取值范围是________
>
m<-2
变式题
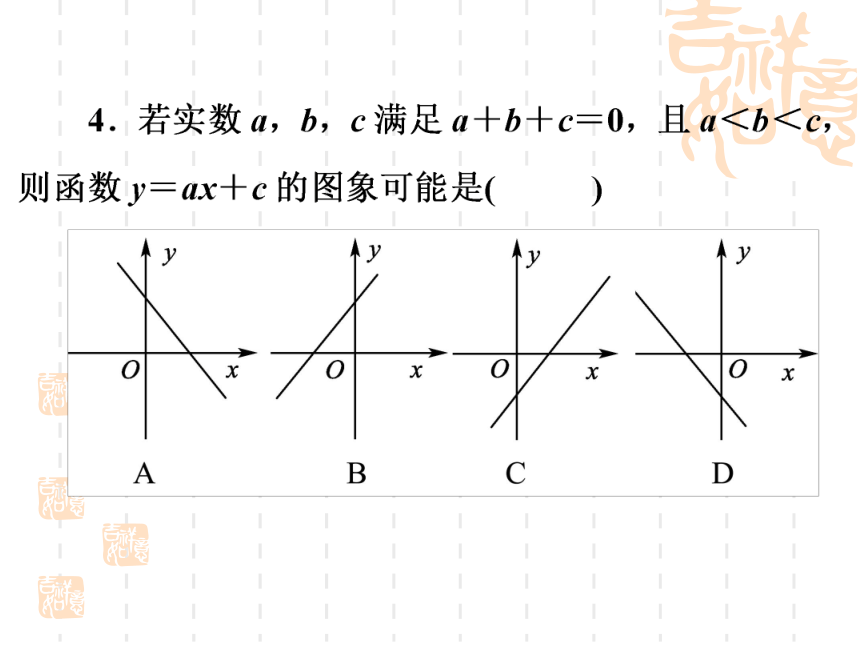
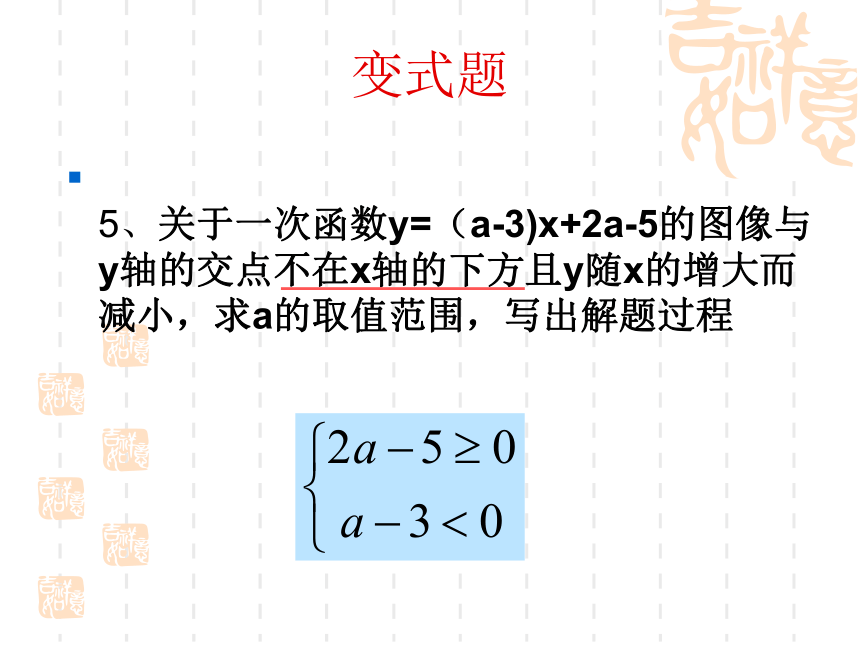
5、关于一次函数y=(a-3)x+2a-5的图像与y轴的交点不在x轴的下方且y随x的增大而减小,求a的取值范围,写出解题过程
命题角度:
1.一次函数的图象的平移规律;
2.求一次函数的图象平移后对应的解析式.
探究二 一次函数的图象的平移
方法点析
直线y=kx+b(k≠0)在平移过程中k值不变.平移的规律是若上下平移,则直接在常数b后加上或减去平移的单位数;若向左(或向右)平移m个单位,则直线y=kx+b(k≠0)变为y=k(x+m)+b(或k(x-m)+b),其口诀是上加下减,左加右减.
区别点的平移是跟着坐标轴方向一致的。
解 析 将直线y=-2x+1的图象向左平移2个单位,再向上平移1个单位,得到的直线的解析式是:y=-2(x+2)+1+1=-2x-2,即y=-2x-2.
例2 在平面直角坐标系中,将直线y=-2x+1的图象向左平移2个单位,再向上平移1个单位,得到的直线的解析式是( )
A.y=-2x-2 B.y=-2x+6
C.y=-2x-4 D.y=-2x+4
A
-8
变式题
变式题
2、把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
C
探究三 求一次函数的解析式及一次函数与坐标轴
围成的面积
例3 已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.
D
y=-4x-2
变式题
变式题
A
变式题
6、在平面直角坐标系中,点O为原点,直线y=kx+b交x轴于点A(-2,0),交y轴于点B.若△AOB的面积为8,则k的值为( )
A.1 B.2 C.-2或4 D.4或-4
D
(-2,0)
(-2,0)
变式题
探究四 一次函数与一次方程(组),一元一次
不等式(组)
命题角度:
1.利用函数图象求二元一次方程(组)的解;
2.利用函数图象解一元一次不等式(组).
例4 一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示.根据图象信息可求得关于x的方程kx+b=0的解为____________.
图10-2
x=-1
0≤x<3
x=3
x>3
变式题
5.如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为______________
-2<X<-1
6、 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
(3)若点C直线AB上,且S△BOC=2,求点C的坐标.
综合运用
甲
乙
丙
A 型汽车每辆运输量(吨)
2
2
—
B 型汽车每辆运输量(吨)
4
—
2
C 型汽车每辆运输量(吨)
—
1
6
例 某公司决定组织21辆汽车装运甲、乙、丙三种土特产共111吨到城市去销售.现有A型、B型、C型三种汽车可供选择.已知每种型号汽车可同时装运两种土特产,且每辆车必须装满.设A型汽车安排 x 辆,B型汽
车安排 y 辆.
(1)求 y 与 x 之间的函数关系式;
(2)如果A,B,C 三种汽车的运费分别为600元/辆、
800元/辆、1 000元/辆,请设计一种运费最省的运输方
案,并求出至少需要运费多少元.
这个问题难在哪里?
建立函数模型
怎样找出变量之间的关系?
2x 吨
2x 吨
4y 吨
2y 吨
(21-x-y)吨
6(21-x-y)吨
111 吨
x 辆
y 辆
(21-x-y)辆
21 辆
(2x+4y)吨
2x+(21-x-y)吨
2y+6(21-x-y)吨
(2x+4y)+2x+21-x-y+2y+6(21-x-y)=111,
y=-3x+36.
总辆数
总吨数
B
乙
A
甲
C
丙
甲
乙
丙
A 型汽车每辆运输量(吨)
2
2
—
B 型汽车每辆运输量(吨)
4
—
2
C 型汽车每辆运输量(吨)
—
1
6
综合运用
(1)求 y 与 x 之间的函数关系式;
解:y 与 x 之间的函数解析式是 y=-3x+36,C型车辆
为(2x -15)辆,
-3x+36≥0,
2x-15≥0.
所以 8≤x≤12.
因为 (x,y 是整数),
综合运用
(2)如果A,B,C 三种汽车的运费分别为600元/辆、
800元/辆、1 000元/辆,请设计一种运费最省的运输方
案,并求出至少需要运费多少元.
解:设总运费为w 元,
则 w=600 x+800(-3x+36)+ 1 000(2x-15),
即 w=200x+13 800,(8≤x≤12).
因为200>0即,w 随着x 的增大而增大,
所以当x=8时,w 最小,w 的最小值为15 400.
即用A 型车8 辆、B 型车12 辆、C 型车1 辆运输时费
用最省,最小运费为15 400 元.
(1)确定自变量与函数;
(2)写出函数的解析式;
(3)求自变量的取值范围;
(4)根据函数性质解释.
反思
在解决这个问题中,是按照怎样的步骤进行的?
课堂小结
建立函数模型的步骤:
(1)确定自变量与函数;(2)写出函数的解析式;(3)求自变量的取值范围;(4)根据函数性质解释.
某些运动变化
的现实问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与方程(组)、
不等式之间的关系
章节总复习
注意:
请同学们先准备好笔和草稿纸。
在需要笔记时候截图,在需要思考时候点暂停视频,解答出来后再点继续观看。
考点1 一次函数与正比例函数的概念
一次
函数
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数
正比例函数
特别地,当b=0时,一次函数y=kx+b变为y=kx(k为常数,k≠0),这时y叫做x的正比例函数(特殊的一次函数)
考点小结
(2)正比例函数与一次函数的性质
函数
字母取值
图象
经过的象限
函数性质
y=kx(k≠0)
k>0
________
y随x增
大而增大
k<0
________
y随x增
大而减小
第一、三
象限
第二、四
象限
考点2 一次函数的图象和性质
y=kx+b(k≠0)
k>0
b>0
________
y随x增
大而增大
k>0
b<0
________
k<0
b>0
________
y随x增
大而减小
k<0
b<0,
________
第一、二、
三象限
第一、三、
四象限
第一、二、
四象限
第二、三、
四象限
考点3 两条直线的位置关系
直线l1:y=k1x+b1和l2:y=k2x+b2的位置关系
相交
________?l1和l2相交
平行
________________?l1和l2平行
k1≠k2
k1=k2,b1≠b2
考点4 两直线的交点坐标及一次函数的图象与坐标
轴围成的三角形的面积
一条直线与坐标轴围成的三角形的面积
解由两个函数解析式组成的二元方程组,方程组的解即两函数图象的交点坐标
一条直线与其他一次函数图象的交点坐标
设x=0,求出对应的y值
一条直线与y轴的交点坐标
设y=0,求出对应的x值
一条直线与x轴的交点坐标
求法
分类
考点5 由待定系数法求一次函数的解析式
待定系数法
考点6 一次函数与一次方程(组)、一元一次不等式(组)
0
>
<
直线和其中一点的关系
直线和其中一段的关系
探究一 一次函数的图象与性质
命题角度:
1.一次函数的概念;
2.一次函数的图象与性质.
例1
如图10-1,一次函数y=(m-2)x-1的图象经过第二、三、四象限,则m的取值范围是( )
A.m>0 B.m<0 C.m>2 D.m<2
D
图10-1
解 析 ∵一次函数y=(m-2)x-1的图象经过第二、三、四象限,∴m-2<0,
解得m<2.
考点训练
2、 一次函数y=(m+2)x+1,若y随x的增大而减小,则m的取值范围是________
>
m<-2
变式题
5、关于一次函数y=(a-3)x+2a-5的图像与y轴的交点不在x轴的下方且y随x的增大而减小,求a的取值范围,写出解题过程
命题角度:
1.一次函数的图象的平移规律;
2.求一次函数的图象平移后对应的解析式.
探究二 一次函数的图象的平移
方法点析
直线y=kx+b(k≠0)在平移过程中k值不变.平移的规律是若上下平移,则直接在常数b后加上或减去平移的单位数;若向左(或向右)平移m个单位,则直线y=kx+b(k≠0)变为y=k(x+m)+b(或k(x-m)+b),其口诀是上加下减,左加右减.
区别点的平移是跟着坐标轴方向一致的。
解 析 将直线y=-2x+1的图象向左平移2个单位,再向上平移1个单位,得到的直线的解析式是:y=-2(x+2)+1+1=-2x-2,即y=-2x-2.
例2 在平面直角坐标系中,将直线y=-2x+1的图象向左平移2个单位,再向上平移1个单位,得到的直线的解析式是( )
A.y=-2x-2 B.y=-2x+6
C.y=-2x-4 D.y=-2x+4
A
-8
变式题
变式题
2、把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
C
探究三 求一次函数的解析式及一次函数与坐标轴
围成的面积
例3 已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.
D
y=-4x-2
变式题
变式题
A
变式题
6、在平面直角坐标系中,点O为原点,直线y=kx+b交x轴于点A(-2,0),交y轴于点B.若△AOB的面积为8,则k的值为( )
A.1 B.2 C.-2或4 D.4或-4
D
(-2,0)
(-2,0)
变式题
探究四 一次函数与一次方程(组),一元一次
不等式(组)
命题角度:
1.利用函数图象求二元一次方程(组)的解;
2.利用函数图象解一元一次不等式(组).
例4 一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示.根据图象信息可求得关于x的方程kx+b=0的解为____________.
图10-2
x=-1
0≤x<3
x=3
x>3
变式题
5.如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为______________
-2<X<-1
6、 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
(3)若点C直线AB上,且S△BOC=2,求点C的坐标.
综合运用
甲
乙
丙
A 型汽车每辆运输量(吨)
2
2
—
B 型汽车每辆运输量(吨)
4
—
2
C 型汽车每辆运输量(吨)
—
1
6
例 某公司决定组织21辆汽车装运甲、乙、丙三种土特产共111吨到城市去销售.现有A型、B型、C型三种汽车可供选择.已知每种型号汽车可同时装运两种土特产,且每辆车必须装满.设A型汽车安排 x 辆,B型汽
车安排 y 辆.
(1)求 y 与 x 之间的函数关系式;
(2)如果A,B,C 三种汽车的运费分别为600元/辆、
800元/辆、1 000元/辆,请设计一种运费最省的运输方
案,并求出至少需要运费多少元.
这个问题难在哪里?
建立函数模型
怎样找出变量之间的关系?
2x 吨
2x 吨
4y 吨
2y 吨
(21-x-y)吨
6(21-x-y)吨
111 吨
x 辆
y 辆
(21-x-y)辆
21 辆
(2x+4y)吨
2x+(21-x-y)吨
2y+6(21-x-y)吨
(2x+4y)+2x+21-x-y+2y+6(21-x-y)=111,
y=-3x+36.
总辆数
总吨数
B
乙
A
甲
C
丙
甲
乙
丙
A 型汽车每辆运输量(吨)
2
2
—
B 型汽车每辆运输量(吨)
4
—
2
C 型汽车每辆运输量(吨)
—
1
6
综合运用
(1)求 y 与 x 之间的函数关系式;
解:y 与 x 之间的函数解析式是 y=-3x+36,C型车辆
为(2x -15)辆,
-3x+36≥0,
2x-15≥0.
所以 8≤x≤12.
因为 (x,y 是整数),
综合运用
(2)如果A,B,C 三种汽车的运费分别为600元/辆、
800元/辆、1 000元/辆,请设计一种运费最省的运输方
案,并求出至少需要运费多少元.
解:设总运费为w 元,
则 w=600 x+800(-3x+36)+ 1 000(2x-15),
即 w=200x+13 800,(8≤x≤12).
因为200>0即,w 随着x 的增大而增大,
所以当x=8时,w 最小,w 的最小值为15 400.
即用A 型车8 辆、B 型车12 辆、C 型车1 辆运输时费
用最省,最小运费为15 400 元.
(1)确定自变量与函数;
(2)写出函数的解析式;
(3)求自变量的取值范围;
(4)根据函数性质解释.
反思
在解决这个问题中,是按照怎样的步骤进行的?
课堂小结
建立函数模型的步骤:
(1)确定自变量与函数;(2)写出函数的解析式;(3)求自变量的取值范围;(4)根据函数性质解释.
某些运动变化
的现实问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与方程(组)、
不等式之间的关系
