人教版九年级下册28章《锐角三角函数复习》课件(共22张PPT)
文档属性
| 名称 | 人教版九年级下册28章《锐角三角函数复习》课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 755.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:43:05 | ||
图片预览






文档简介
课题
28章锐角三角函数
学习目标
1. 巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数.
2. 熟记30°,45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.
3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形.
4.会用解直角三角形的有关知识解决简单的实际问题.
知识回顾1
一.锐角三角函数的概念
正弦:把锐角A的__________的比叫做∠A的正弦,记作
余弦:把锐角A的__________的比叫做∠A的余弦,记作
正切:把锐角A的__________的比叫做∠A的正切,记作
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
对边与斜边
邻边与斜边
对边与邻边
sinA=cos(90°- A )=cosB
cosA=sin(90°- A)=sinB
c
A
B
C
b
a
同角的正 弦余弦与正切和余切之间的关系
互余两个角的三角函数关系
同角的正弦余弦平方和等于1
同角的正切余切互为倒数
练 习 2
二、几个重要关系式
tanA·cotA=1
sin2A+cos2A=1
⑴ 已知:Rt△ABC中,∠C=90°∠A为锐角,且tanA=0.6,tanB=( ).
3/5
⑵ sin2A+tanAtanB -2+cos2A=( )
0
⑶ tan44°tan46°=( ).
1
(4)tan29°tan60°tan61°=( ).
(5) sin53°cos37°+cos53°sin37°
=( )
1
tanA=
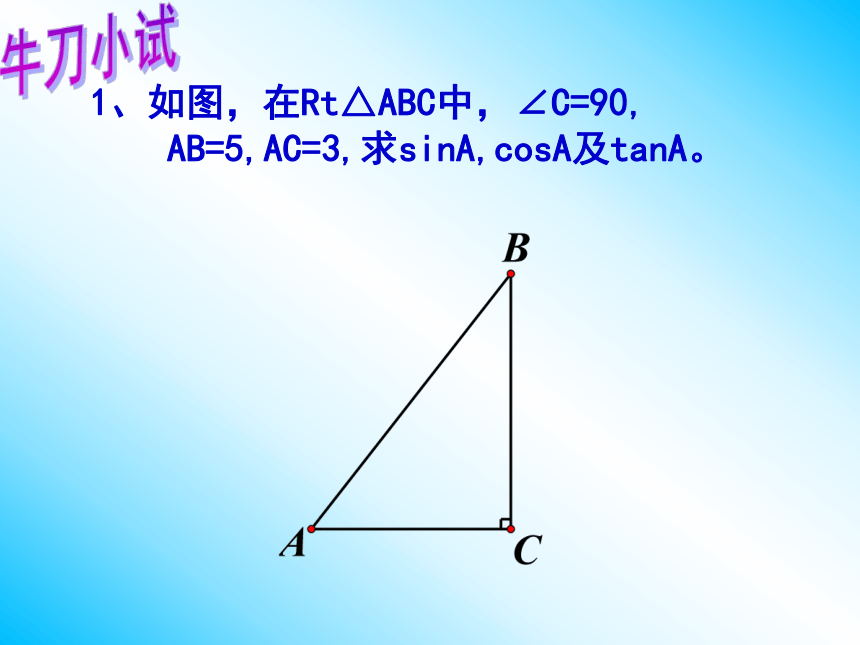
1、如图,在Rt△ABC中,∠C=90,
AB=5,AC=3,求sinA,cosA及tanA。
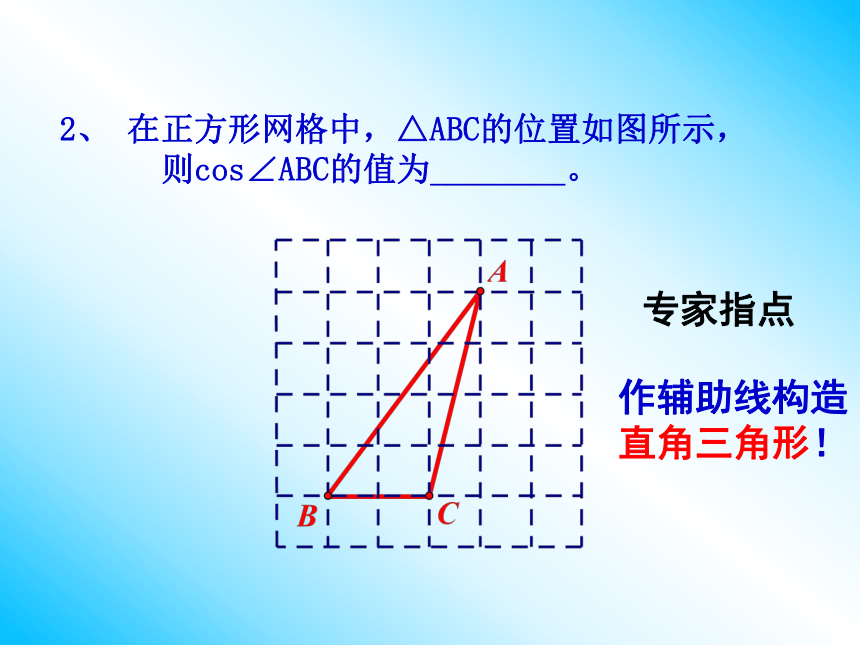
2、 在正方形网格中,△ABC的位置如图所示,
则cos∠ABC的值为________。
作辅助线构造直角三角形!
专家指点
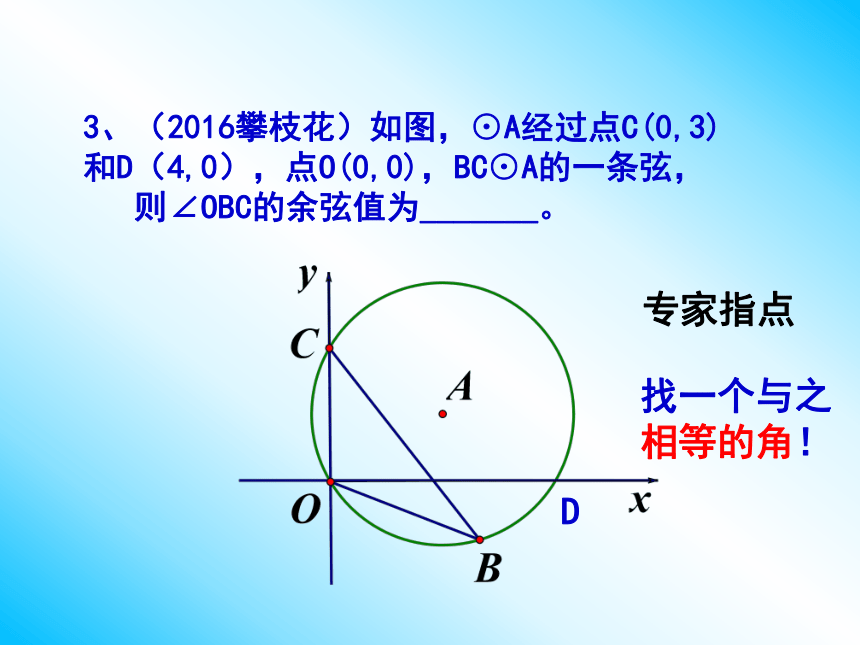
3、(2016攀枝花)如图,⊙A经过点C(0,3)和D(4,0),点O(0,0),BC⊙A的一条弦,
则∠OBC的余弦值为_______。
专家指点
找一个与之
相等的角!
D
知识回顾2
二.特殊角的三角函数值
锐角的三角函数值有何变化规律呢?
正切值和正弦值都随着锐角度数的增大而_____;
余弦值随着锐角度数的增大而_____.
增大
减小
sinA =
cosA =
cosB
sinB
☆ 应用练习
一.已知角,求值
(2)2sin30°+3tan30°+tan45°
(3)cos245°+ tan60°cos30°
(1)tan45°-sin60°cos30°
(4)2sin60°-3tan30°-(π-cos30°)+(-1)2012
☆ 应用练习
二.已知值,求角
(1)已知 sinA= ,求锐角A .
(2)已知2cosA - = 0 , 求锐角A.
(3)已知 tan( ∠A+20°)= ,求锐角A .
(4)在△ABC中, ∠ B、 ∠ C均为锐角,且
,求∠A的度数。
☆ 应用练习
三.比较大小
(1)sin250____sin430
(2)cos70____cos80
(3)sin400____cos600
(4)tan480____tan400
知识回顾3
三.解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
归纳:只要知道其中的2个元素(至少有一个是____),就可以求出其余3个未知元素.
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
边
知识回顾4
四.解直角三角形的应用
1.仰角和俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做____;
从上往下看,视线与水平线的夹角叫做____。
铅直线
水平线
视线
视线
仰角
俯角
仰角
俯角
坡度:坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,即:
2.坡角、坡度
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
h
l
(2016重庆A卷)11.某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为( )(参考数据:sin36°≈0.95,cos36°≈0.81,tan36°≈0.73)
A.8.1米 B.17.2米 C.19.7米 D.25.5米
2.海中有一个小岛A,它的周围6海里内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
C
D
30°
练 习
3.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示.BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造.经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米(结果保留根号)?
G
F
试一试:2016资阳)如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
锐角三角函数
1.锐角三角函数的定义
⑴正弦
⑵余弦
⑶正切
2.30°、45°、60°特殊角的三角函数值
3.解直角三角形
⑴定义
⑵解直角三角形的依据
①三边间关系
②锐角间关系
③边角间关系
⑶解直角三角形在实际问题中
的应用
及时反馈1
1.若 ,则锐角α=
2.若 ,则锐角α=
3.计算:
45°
80°
4.如图,在Rt△ABC中,∠C=90,b= ,c=4.
则a= ,∠B= ,∠A= .
A
B
C
2
60°
30°
D
5.如果
那么△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
28章锐角三角函数
学习目标
1. 巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数.
2. 熟记30°,45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.
3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形.
4.会用解直角三角形的有关知识解决简单的实际问题.
知识回顾1
一.锐角三角函数的概念
正弦:把锐角A的__________的比叫做∠A的正弦,记作
余弦:把锐角A的__________的比叫做∠A的余弦,记作
正切:把锐角A的__________的比叫做∠A的正切,记作
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
对边与斜边
邻边与斜边
对边与邻边
sinA=cos(90°- A )=cosB
cosA=sin(90°- A)=sinB
c
A
B
C
b
a
同角的正 弦余弦与正切和余切之间的关系
互余两个角的三角函数关系
同角的正弦余弦平方和等于1
同角的正切余切互为倒数
练 习 2
二、几个重要关系式
tanA·cotA=1
sin2A+cos2A=1
⑴ 已知:Rt△ABC中,∠C=90°∠A为锐角,且tanA=0.6,tanB=( ).
3/5
⑵ sin2A+tanAtanB -2+cos2A=( )
0
⑶ tan44°tan46°=( ).
1
(4)tan29°tan60°tan61°=( ).
(5) sin53°cos37°+cos53°sin37°
=( )
1
tanA=
1、如图,在Rt△ABC中,∠C=90,
AB=5,AC=3,求sinA,cosA及tanA。
2、 在正方形网格中,△ABC的位置如图所示,
则cos∠ABC的值为________。
作辅助线构造直角三角形!
专家指点
3、(2016攀枝花)如图,⊙A经过点C(0,3)和D(4,0),点O(0,0),BC⊙A的一条弦,
则∠OBC的余弦值为_______。
专家指点
找一个与之
相等的角!
D
知识回顾2
二.特殊角的三角函数值
锐角的三角函数值有何变化规律呢?
正切值和正弦值都随着锐角度数的增大而_____;
余弦值随着锐角度数的增大而_____.
增大
减小
sinA =
cosA =
cosB
sinB
☆ 应用练习
一.已知角,求值
(2)2sin30°+3tan30°+tan45°
(3)cos245°+ tan60°cos30°
(1)tan45°-sin60°cos30°
(4)2sin60°-3tan30°-(π-cos30°)+(-1)2012
☆ 应用练习
二.已知值,求角
(1)已知 sinA= ,求锐角A .
(2)已知2cosA - = 0 , 求锐角A.
(3)已知 tan( ∠A+20°)= ,求锐角A .
(4)在△ABC中, ∠ B、 ∠ C均为锐角,且
,求∠A的度数。
☆ 应用练习
三.比较大小
(1)sin250____sin430
(2)cos70____cos80
(3)sin400____cos600
(4)tan480____tan400
知识回顾3
三.解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
归纳:只要知道其中的2个元素(至少有一个是____),就可以求出其余3个未知元素.
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
边
知识回顾4
四.解直角三角形的应用
1.仰角和俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做____;
从上往下看,视线与水平线的夹角叫做____。
铅直线
水平线
视线
视线
仰角
俯角
仰角
俯角
坡度:坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,即:
2.坡角、坡度
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
h
l
(2016重庆A卷)11.某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为( )(参考数据:sin36°≈0.95,cos36°≈0.81,tan36°≈0.73)
A.8.1米 B.17.2米 C.19.7米 D.25.5米
2.海中有一个小岛A,它的周围6海里内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
C
D
30°
练 习
3.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示.BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造.经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米(结果保留根号)?
G
F
试一试:2016资阳)如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
锐角三角函数
1.锐角三角函数的定义
⑴正弦
⑵余弦
⑶正切
2.30°、45°、60°特殊角的三角函数值
3.解直角三角形
⑴定义
⑵解直角三角形的依据
①三边间关系
②锐角间关系
③边角间关系
⑶解直角三角形在实际问题中
的应用
及时反馈1
1.若 ,则锐角α=
2.若 ,则锐角α=
3.计算:
45°
80°
4.如图,在Rt△ABC中,∠C=90,b= ,c=4.
则a= ,∠B= ,∠A= .
A
B
C
2
60°
30°
D
5.如果
那么△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
