人教版七年级数学下册 第九章 一元一次不等式(组)整数解专题 (46张PPT)
文档属性
| 名称 | 人教版七年级数学下册 第九章 一元一次不等式(组)整数解专题 (46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览






文档简介
不等式组有整数解题型
中学数学 傅老师
课前准备
1、什么是不等式组的解集?
2、观察下列不等式组,并找出它们的解集。
⑸X>3和x>3
⑹X>3和x≥3
⑴X>3和x>4
⑺X≥3和x≤3
⑵X≤3和x<4
⑶X>3和x<4
⑷X<3和x>4
x>4
X≤3
无解
3< x<4
x>3
x>3
X=3
已知不等式 2x-1>1与不等式 x<a 组成的不等式组有解,求a的取值范围。
分析:第一个不等式的解集为x>1,第二个不等式的解集为x<a,此不等式组有解,说明两个不等式的解集有公共部分。
接下来,我们数轴上表示两个不等式的解集,分析a的范围。
0
1
a
a
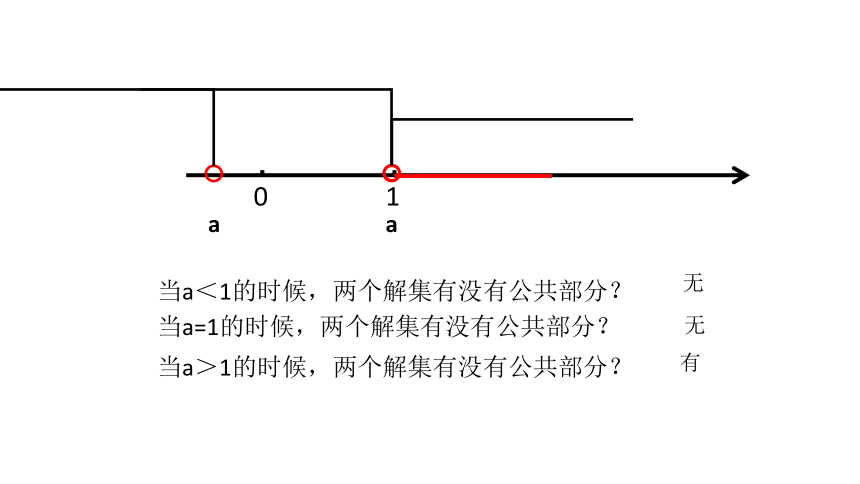
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
无
有
0
1
a
a
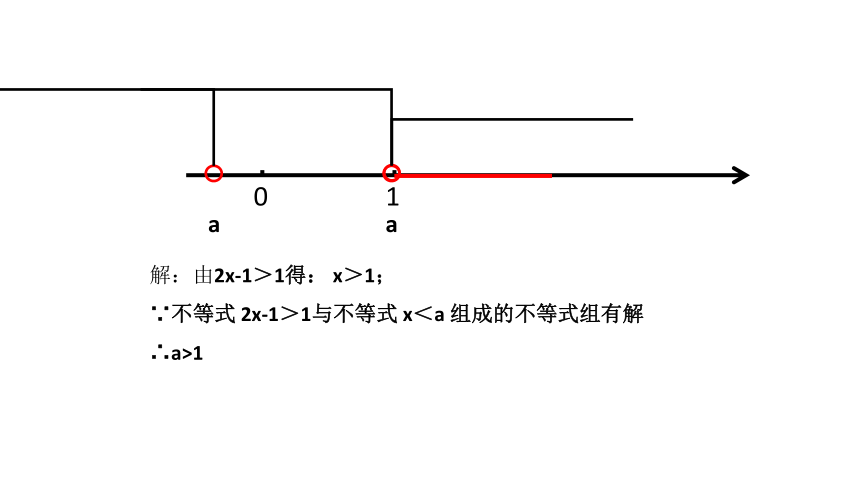
解:由2x-1>1得: x>1;
∵不等式 2x-1>1与不等式 x<a 组成的不等式组有解
∴a>1
总结
1、先解出不等式组组中的每个不等式的解集。
2、然后在数轴上表示出这些解集,利用数形结合的数学思想进行分类讨论。
例如:在本题中,我们分别谈论a>1,a=1,a<1三种情况下两个不等式的解集是否有公共部分。
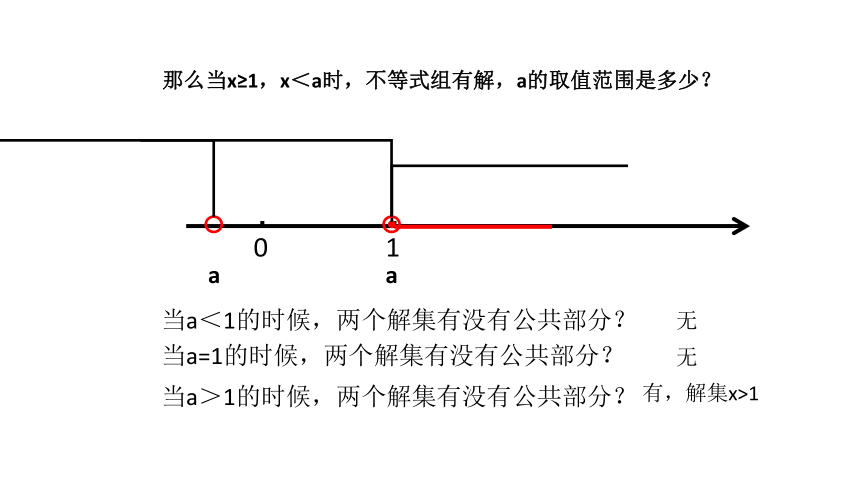
那么当x≥1,x<a时,不等式组有解,a的取值范围是多少?
0
1
a
a
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
无
有,解集x>1
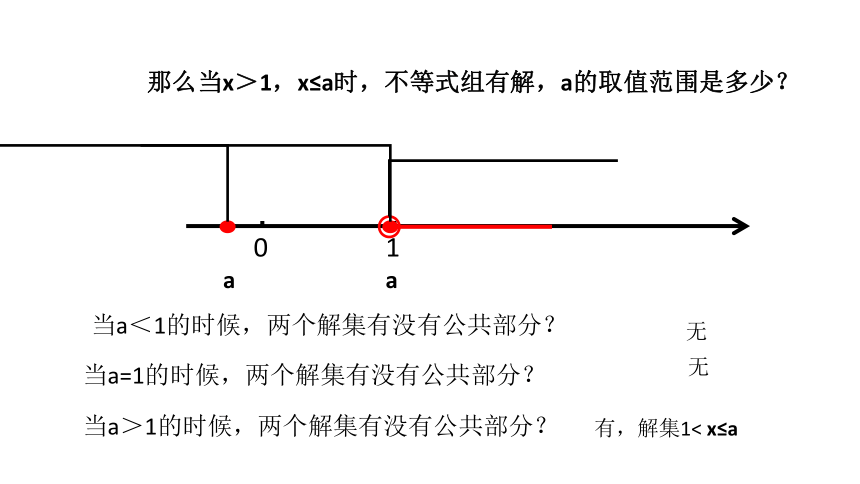
那么当x>1,x≤a时,不等式组有解,a的取值范围是多少?
0
1
a
a
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
无
有,解集1< x≤a
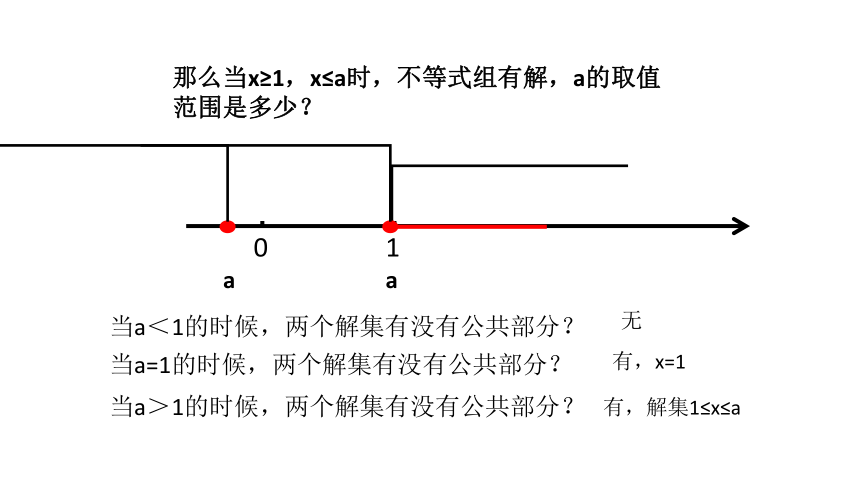
那么当x≥1,x≤a时,不等式组有解,a的取值范围是多少?
0
1
a
a
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
有,x=1
有,解集1≤x≤a
学以致用
已知一个未知数x,它有无数个值可以让不等式3x-1<-4和不等式2x≥a-2都成立,求a的取值范围。
解:由3x-1<-4得:x<-1
由2x≥a-2得:
∵不等式3x-1<-4和不等式2x≥a-2有解
a-2<-2
?
∴
即
拓展延伸
1、x>3与x>b组成的不等式组有解,求b的取值范围
2、x<3与x<b组成的不等式组有解,求b的取值范围
4
0
3
2
1
5
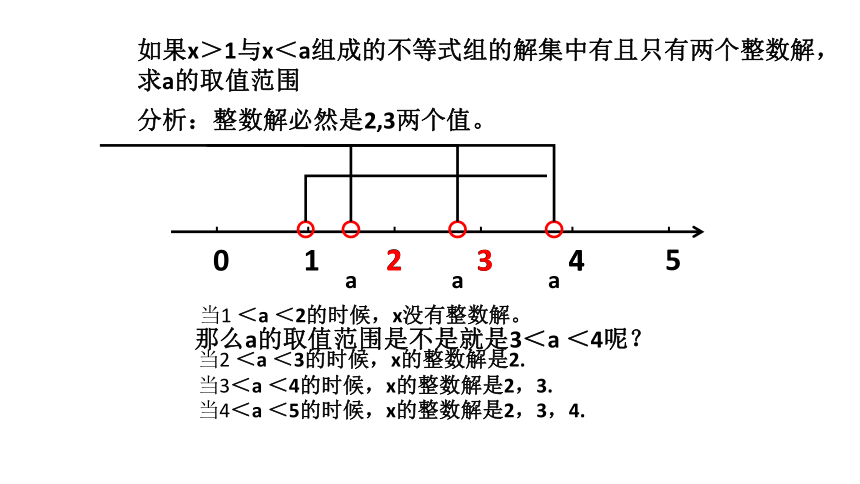
如果x>1与x<a组成的不等式组的解集中有且只有两个整数解,求a的取值范围
a
2
a
3
a
4
当1 <a <2的时候,x没有整数解。
当2 <a <3的时候,x的整数解是2.
当3<a <4的时候,x的整数解是2,3.
当4<a <5的时候,x的整数解是2,3,4.
那么a的取值范围是不是就是3<a <4呢?
分析:整数解必然是2,3两个值。
讨论:
假设a=3,能不能满足题意?
假设a=4,能不能满足题意?
0
1
5
2
3
4
a
2
a
3
从图形中,我们可以很容易发现:当a=3的时候不能满足题意;当a=4的时候,满足题意。
综上:当3<a ≤4的时候,x的整数解是2,3.
总结:
1、先确定整数解是哪些。例如:本题中的整数解是2,3.
2、确定a在哪两个整数之间。例如:本题中只有3<a ≤4的时候,x的整数解才有可能是2和3.
3、判断a能不能取到边界值。(方法:假设能取到边界值)例如:本题中假设a=3,发现不成立。假设a=4,假设成立。
学以致用
用你本节课所学的知识,解决下面的题目!
1、如果x≥1与x<a组成的不等式组的解集中有且只有两个整数解,求a的取值范围。
2、如果x≥1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围。
3、如果x>1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围。
4
0
3
2
1
5
1.如果x≥1与x<a组成的不等式组的解集中有且只有两个整数解,求a的取值范围.
a
2
a
3
a
4
当1 < a ≤ 2的时候,x的整数解是x=1;
当2 < a ≤ 3的时候,x的整数解是1,2;
当3 < a ≤ 4的时候,x的整数解是1,2,3.
当4 < a ≤ 5的时候,x的整数解是1, 2,3,4.
那么a的取值范围是不是就是3 ≤ a <4呢?
分析:整数解必然是1,2两个值。
综上:当2 < a ≤ 3时,x的整数解是1,2.
4
0
3
2
1
5
2.如果x≥1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围.
a
2
a
3
a
4
当1 < a ≤ 2的时候, x的整数解是1,2 ;
当2 < a ≤ 3的时候,x的整数解是1,2, 3;
当3 ≤ a <4的时候,x的整数解是1,2,3.
那么a的取值范围是不是就是1 ≤ a <2呢?
分析:整数解必然是1,2两个值。
综上:当1 < a ≤ 2 时,x的整数解是1,2.
当a=1 的时候,x的整数解是1;
4
0
3
2
1
5
3.如果x>1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围.
a
2
a
3
a
4
当1 < a <2的时候,x没有整数解;
当2 ≤ a <3的时候,x的整数解是2.
当3 ≤ a <4的时候,x的整数解是2,3.
那么a的取值范围是不是就是3 ≤ a <4呢?
分析:整数解必然是2,3两个值。
综上:当3 ≤ a <4 时,x的整数解是2,3.
当4 ≤ a <5的时候,x的整数解是2,3,4.
4、已知x≥a与x<b组成的不等式组有解,求a,b的大小关系。
解: ∵ x≥a与x<b组成的不等式组有解
∴b>a
5、已知x≥a与x<b组成的不等式组有解,且只有3,4,5三个整数解,求a,b的取值范围。
解: 由题意,得:2 5
专题 一元一次不等式的特殊解
1.方程(组)的解满足特定的要求.这类问题的解题思路是先用含字母的式子来表示方程(组)的解,再依据要求列出关于字母的不等式(组)求解即可.
2.含字母的不等式(组)的解集满足特定的要求.这类问题的解题思路是先用含字母的式子表示出不等式(组)的解集,再根据要求列出关于字母的不等式(组)求解即可.
解:不等式组的解集为-1≤x<1,
所以不等式组的整数解为-1和0.
解:不等式组的解集为0≤x≤3,
所以不等式组的整数解为0,1,2,3,整数解之和为0+1+2+3=6.
解:解该不等式组得-2所以不等式组的两个整数解为-1,0.
所以0≤a+4<1,所以实数a的取值范围为-4≤a<-3.
类型3 与方程(组)综合求不等式(组)的特殊解
4.已知整数x满足不等式3x-4≤6x-2和不等式 .并且满足方程3(x+m)-5m+2=0,求m的值.
解:联立两个不等式,解得- ≤x<1,所以整数x=0,
所以3m-5m+2=0,解得m=1.
(1)求m的取值范围;
(2)化简:|m-3|-|m+2|;
(3)在(1)的取值范围内,当m为何整数时,不等式(2m-1)x<2m-1的解为x>1?
1.满足-1≤x≤2的所有整数为__________________________.
2.满足-1<x≤2的所有整数为__________________________.
3.请写出一个只含有三个整数-1,-2,-3的解_________________________.
0,1,2
-1,0,1,2
-3≤x≤-1
4.不等式2x-1≥3x-3的正整数解为 __________________________.
5.使不等式4x+3<x+6成立的最大整数解为 ______________________.
6, 不等式3(x-1)≤5-x的非负整数解为 __________________________.
7使不等式x-2≥-3与2x+3<5同时成立的x的整数值是______________.
1,2
0
0,1,2
-1,0
8.若不等式3x-m≤0的正整数解为1、2、3,则m的范围是_____________.
9. 若不等式3x-m<0的正整数解为1、2、3,则m的范围是_________.
10.关于x的不等式x-m>0,恰有两个负整数解,则m的范围是_________________.
11. 不等式5x-3<3x+5的所有正整数解的和为______________.
9≤m<12
9-3≤ m < -2
6
12.已知满足不等式3(x-2)+5<4(x-1)+6的最小整数解是方程2x-ax=3的解,则a的值为______________.
解:由不等式3(x-2)+5<4(x-1)+6得:x>3
∴满足不等式3(x-2)+5<4(x-1)+6的最小整数解是x=4
∴把x=4代入方程2x-ax=3得:
8-4a=3
13.解不等式
≤
并把解集表示在数轴上,写出最小整数解。
解:
14.x取哪些整数时,不等式5x+2>3(x-1)与 都成立.
≤
解:
15.若关于x,y的二元一次方程组
的解满足x-y>-3.5,求满足条件的m的所有正整数解.
解:
同一题型:
解:
16.
解:
17.不等式组
,有解,求a的取值范围。
解:
18.不等式组
,有4个整数解,求a的取值范围。
解:
解:
解:
中学数学 傅老师
课前准备
1、什么是不等式组的解集?
2、观察下列不等式组,并找出它们的解集。
⑸X>3和x>3
⑹X>3和x≥3
⑴X>3和x>4
⑺X≥3和x≤3
⑵X≤3和x<4
⑶X>3和x<4
⑷X<3和x>4
x>4
X≤3
无解
3< x<4
x>3
x>3
X=3
已知不等式 2x-1>1与不等式 x<a 组成的不等式组有解,求a的取值范围。
分析:第一个不等式的解集为x>1,第二个不等式的解集为x<a,此不等式组有解,说明两个不等式的解集有公共部分。
接下来,我们数轴上表示两个不等式的解集,分析a的范围。
0
1
a
a
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
无
有
0
1
a
a
解:由2x-1>1得: x>1;
∵不等式 2x-1>1与不等式 x<a 组成的不等式组有解
∴a>1
总结
1、先解出不等式组组中的每个不等式的解集。
2、然后在数轴上表示出这些解集,利用数形结合的数学思想进行分类讨论。
例如:在本题中,我们分别谈论a>1,a=1,a<1三种情况下两个不等式的解集是否有公共部分。
那么当x≥1,x<a时,不等式组有解,a的取值范围是多少?
0
1
a
a
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
无
有,解集x>1
那么当x>1,x≤a时,不等式组有解,a的取值范围是多少?
0
1
a
a
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
无
有,解集1< x≤a
那么当x≥1,x≤a时,不等式组有解,a的取值范围是多少?
0
1
a
a
当a<1的时候,两个解集有没有公共部分?
当a=1的时候,两个解集有没有公共部分?
当a>1的时候,两个解集有没有公共部分?
无
有,x=1
有,解集1≤x≤a
学以致用
已知一个未知数x,它有无数个值可以让不等式3x-1<-4和不等式2x≥a-2都成立,求a的取值范围。
解:由3x-1<-4得:x<-1
由2x≥a-2得:
∵不等式3x-1<-4和不等式2x≥a-2有解
a-2<-2
?
∴
即
拓展延伸
1、x>3与x>b组成的不等式组有解,求b的取值范围
2、x<3与x<b组成的不等式组有解,求b的取值范围
4
0
3
2
1
5
如果x>1与x<a组成的不等式组的解集中有且只有两个整数解,求a的取值范围
a
2
a
3
a
4
当1 <a <2的时候,x没有整数解。
当2 <a <3的时候,x的整数解是2.
当3<a <4的时候,x的整数解是2,3.
当4<a <5的时候,x的整数解是2,3,4.
那么a的取值范围是不是就是3<a <4呢?
分析:整数解必然是2,3两个值。
讨论:
假设a=3,能不能满足题意?
假设a=4,能不能满足题意?
0
1
5
2
3
4
a
2
a
3
从图形中,我们可以很容易发现:当a=3的时候不能满足题意;当a=4的时候,满足题意。
综上:当3<a ≤4的时候,x的整数解是2,3.
总结:
1、先确定整数解是哪些。例如:本题中的整数解是2,3.
2、确定a在哪两个整数之间。例如:本题中只有3<a ≤4的时候,x的整数解才有可能是2和3.
3、判断a能不能取到边界值。(方法:假设能取到边界值)例如:本题中假设a=3,发现不成立。假设a=4,假设成立。
学以致用
用你本节课所学的知识,解决下面的题目!
1、如果x≥1与x<a组成的不等式组的解集中有且只有两个整数解,求a的取值范围。
2、如果x≥1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围。
3、如果x>1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围。
4
0
3
2
1
5
1.如果x≥1与x<a组成的不等式组的解集中有且只有两个整数解,求a的取值范围.
a
2
a
3
a
4
当1 < a ≤ 2的时候,x的整数解是x=1;
当2 < a ≤ 3的时候,x的整数解是1,2;
当3 < a ≤ 4的时候,x的整数解是1,2,3.
当4 < a ≤ 5的时候,x的整数解是1, 2,3,4.
那么a的取值范围是不是就是3 ≤ a <4呢?
分析:整数解必然是1,2两个值。
综上:当2 < a ≤ 3时,x的整数解是1,2.
4
0
3
2
1
5
2.如果x≥1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围.
a
2
a
3
a
4
当1 < a ≤ 2的时候, x的整数解是1,2 ;
当2 < a ≤ 3的时候,x的整数解是1,2, 3;
当3 ≤ a <4的时候,x的整数解是1,2,3.
那么a的取值范围是不是就是1 ≤ a <2呢?
分析:整数解必然是1,2两个值。
综上:当1 < a ≤ 2 时,x的整数解是1,2.
当a=1 的时候,x的整数解是1;
4
0
3
2
1
5
3.如果x>1与x≤a组成的不等式组的解集中有且只有两个整数解,求a的取值范围.
a
2
a
3
a
4
当1 < a <2的时候,x没有整数解;
当2 ≤ a <3的时候,x的整数解是2.
当3 ≤ a <4的时候,x的整数解是2,3.
那么a的取值范围是不是就是3 ≤ a <4呢?
分析:整数解必然是2,3两个值。
综上:当3 ≤ a <4 时,x的整数解是2,3.
当4 ≤ a <5的时候,x的整数解是2,3,4.
4、已知x≥a与x<b组成的不等式组有解,求a,b的大小关系。
解: ∵ x≥a与x<b组成的不等式组有解
∴b>a
5、已知x≥a与x<b组成的不等式组有解,且只有3,4,5三个整数解,求a,b的取值范围。
解: 由题意,得:2
专题 一元一次不等式的特殊解
1.方程(组)的解满足特定的要求.这类问题的解题思路是先用含字母的式子来表示方程(组)的解,再依据要求列出关于字母的不等式(组)求解即可.
2.含字母的不等式(组)的解集满足特定的要求.这类问题的解题思路是先用含字母的式子表示出不等式(组)的解集,再根据要求列出关于字母的不等式(组)求解即可.
解:不等式组的解集为-1≤x<1,
所以不等式组的整数解为-1和0.
解:不等式组的解集为0≤x≤3,
所以不等式组的整数解为0,1,2,3,整数解之和为0+1+2+3=6.
解:解该不等式组得-2
所以0≤a+4<1,所以实数a的取值范围为-4≤a<-3.
类型3 与方程(组)综合求不等式(组)的特殊解
4.已知整数x满足不等式3x-4≤6x-2和不等式 .并且满足方程3(x+m)-5m+2=0,求m的值.
解:联立两个不等式,解得- ≤x<1,所以整数x=0,
所以3m-5m+2=0,解得m=1.
(1)求m的取值范围;
(2)化简:|m-3|-|m+2|;
(3)在(1)的取值范围内,当m为何整数时,不等式(2m-1)x<2m-1的解为x>1?
1.满足-1≤x≤2的所有整数为__________________________.
2.满足-1<x≤2的所有整数为__________________________.
3.请写出一个只含有三个整数-1,-2,-3的解_________________________.
0,1,2
-1,0,1,2
-3≤x≤-1
4.不等式2x-1≥3x-3的正整数解为 __________________________.
5.使不等式4x+3<x+6成立的最大整数解为 ______________________.
6, 不等式3(x-1)≤5-x的非负整数解为 __________________________.
7使不等式x-2≥-3与2x+3<5同时成立的x的整数值是______________.
1,2
0
0,1,2
-1,0
8.若不等式3x-m≤0的正整数解为1、2、3,则m的范围是_____________.
9. 若不等式3x-m<0的正整数解为1、2、3,则m的范围是_________.
10.关于x的不等式x-m>0,恰有两个负整数解,则m的范围是_________________.
11. 不等式5x-3<3x+5的所有正整数解的和为______________.
9≤m<12
9
6
12.已知满足不等式3(x-2)+5<4(x-1)+6的最小整数解是方程2x-ax=3的解,则a的值为______________.
解:由不等式3(x-2)+5<4(x-1)+6得:x>3
∴满足不等式3(x-2)+5<4(x-1)+6的最小整数解是x=4
∴把x=4代入方程2x-ax=3得:
8-4a=3
13.解不等式
≤
并把解集表示在数轴上,写出最小整数解。
解:
14.x取哪些整数时,不等式5x+2>3(x-1)与 都成立.
≤
解:
15.若关于x,y的二元一次方程组
的解满足x-y>-3.5,求满足条件的m的所有正整数解.
解:
同一题型:
解:
16.
解:
17.不等式组
,有解,求a的取值范围。
解:
18.不等式组
,有4个整数解,求a的取值范围。
解:
解:
解:
