人教版七年级数学下册 8.3:实际问题与二元一次方程组 课件(共19 张ppt)
文档属性
| 名称 | 人教版七年级数学下册 8.3:实际问题与二元一次方程组 课件(共19 张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 566.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览






文档简介
8.3 实际问题与
二元一次方程组
利用一元一次方程组解决实际问题的一般步骤是怎样的?与同伴交流一下.
审 清题意,找出等量关系;
设 未知数x和y;
列 出二元一次方程组;
解 方程组;
检 验;
答 题.
知识回顾
(1)30头大牛1天所需饲料+15头小牛1天所需饲料=1天的饲料总量;
(2)42头大牛1天所需饲料+20头小牛1天所需饲料=后来1天的饲料总量.
等量关系:
【例1】养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验他的估计吗?
探究新知
解:设平均每只母牛1天需用饲料x千克,小牛需用y千克,则:
探究新知
解得
所以平均每只母牛1天需用饲料20千克,小牛需用5千克.
答:饲养员大叔对大牛的食量估计 ,对小牛的食量估计 。
较准
偏高
【例1】养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验他的估计吗?
某校环保小组成员收集废电池,第一天收集了一号电池4节,五号电池5节,总重为460克,第二天收集了一号电池2节,五号电池3节,总重为240克,则一号电池和五号电池每节分别重多少克?
解:设一号电池和五号电池每节分别重x克、y克,
则可列方程组
2x+3y=240.
4x+5y=460,
解得
x=90,
y=20.
答:一号电池和五号电池每节分别重90克、20克.
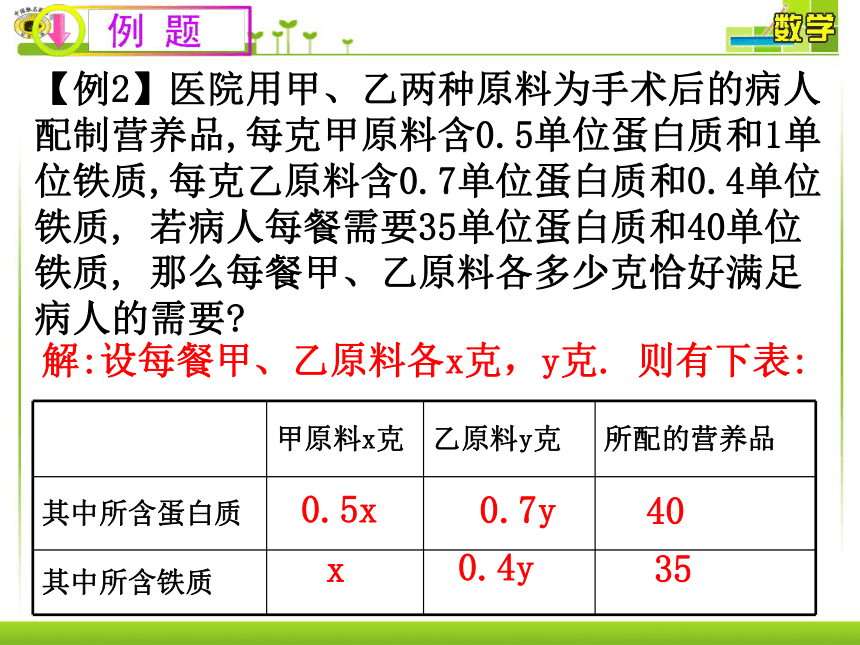
解:设每餐甲、乙原料各x克,y克. 则有下表:
甲原料x克
乙原料y克
所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
【例2】医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要?
根据题意,得方程组
5x+7y=350, ①
5x+2y=200. ②
0.5x+0.7y=35,
x+0.4y=40.
化简,得
①- ②,得 5y=150
y=30
把y=30代入①,得x=28
答:每餐甲原料28克,乙原料30克恰好满足病人的需要.
解:设每餐甲、乙原料各x克,y克. 则有下表:
解:设一、二班的学生分别为x名,y名.
一班
二班
两班总和
学生数
达标学生数
x
y
100
87.5﹪x
75﹪y
81﹪×100
一、二班共有100名学生,他们的体育达标率(达到标准的百分率)为81﹪,如果一班学生的体育达标率为87.5﹪,二班学生的体育达标率为75﹪,那么一、二班的学生数各是多少?
根据题意,得方程组
x+y=100,
87.5﹪x+75﹪y=81﹪×100.
解得
x=48,
y=52.
答:一、二班的学生数分别为48名和52名.
解:设一、二班的学生分别为x名,y名.
鸡兔同笼,共有12个头,36只腿,则笼中有
只鸡, 只兔;
甲、乙两数之和是42,甲数的3倍等于乙数的4倍,求甲、乙两数各是多少?若设甲数为
x,乙数为y,依题意可列方程组 。
6
6
能力练习
3.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为( )
c
一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为( )
A、X=3,y=2 B、x=14,y=1
C、x=15,y=1 D、x=14,y=2
B
列二元一次方程组解决实际问题的一般步骤
(1)审题.
(2)设两个未知数,找两个等量关系.
(3)根据等量关系列方程,联立方程组.
(4)解方程组.
(5)检验并作答.
通过本课时的学习,我们需要掌握:
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
检 验
实际问题
的答案
巩固提高
练一练,相信你能行
某中学七年级(3)班51名同学为“希望工程”捐款,共捐款181元,捐款情况如下表,表格中捐款3元和4元的人数不小心被墨水污染已看不清楚.设捐款3元的有x名同学,捐款4元的有y名同学,
根据题意,可列方程组为:______________.
巩固提高
做一做
“五一期间”,你们一家5个大人和3个小孩去开心乐园,买门票共花了68元.我们家也是去开心乐园,不过比你家多2个大人,多1个小孩,门票共花了94元.如果我们家9个大人和5个小孩去开心乐园,买门票需要多少元呢?
设大人的门票每张为x元,小孩的门票每张为y元.列方程组得
努力提高自我
试一试 :某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由。
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=1680
2x+y=2280
解得:
x=960
y=360
(2)若7个餐厅同时开放,则有
5×960+2×360=5320
答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐。 (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐。
5320>5300
依题意得
想一想 :某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售。该公司的加工能力是:每天可以精加工6吨或粗加工16吨。现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?
解:设该公司应安排x天精加工,y天粗加工,
x+y=15
6x+16y=140
解 得:
x=10
y=5
答:该公司应安排x10天精加工,5天粗加工。
拓展延伸
依题意得
二元一次方程组
利用一元一次方程组解决实际问题的一般步骤是怎样的?与同伴交流一下.
审 清题意,找出等量关系;
设 未知数x和y;
列 出二元一次方程组;
解 方程组;
检 验;
答 题.
知识回顾
(1)30头大牛1天所需饲料+15头小牛1天所需饲料=1天的饲料总量;
(2)42头大牛1天所需饲料+20头小牛1天所需饲料=后来1天的饲料总量.
等量关系:
【例1】养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验他的估计吗?
探究新知
解:设平均每只母牛1天需用饲料x千克,小牛需用y千克,则:
探究新知
解得
所以平均每只母牛1天需用饲料20千克,小牛需用5千克.
答:饲养员大叔对大牛的食量估计 ,对小牛的食量估计 。
较准
偏高
【例1】养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验他的估计吗?
某校环保小组成员收集废电池,第一天收集了一号电池4节,五号电池5节,总重为460克,第二天收集了一号电池2节,五号电池3节,总重为240克,则一号电池和五号电池每节分别重多少克?
解:设一号电池和五号电池每节分别重x克、y克,
则可列方程组
2x+3y=240.
4x+5y=460,
解得
x=90,
y=20.
答:一号电池和五号电池每节分别重90克、20克.
解:设每餐甲、乙原料各x克,y克. 则有下表:
甲原料x克
乙原料y克
所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
【例2】医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要?
根据题意,得方程组
5x+7y=350, ①
5x+2y=200. ②
0.5x+0.7y=35,
x+0.4y=40.
化简,得
①- ②,得 5y=150
y=30
把y=30代入①,得x=28
答:每餐甲原料28克,乙原料30克恰好满足病人的需要.
解:设每餐甲、乙原料各x克,y克. 则有下表:
解:设一、二班的学生分别为x名,y名.
一班
二班
两班总和
学生数
达标学生数
x
y
100
87.5﹪x
75﹪y
81﹪×100
一、二班共有100名学生,他们的体育达标率(达到标准的百分率)为81﹪,如果一班学生的体育达标率为87.5﹪,二班学生的体育达标率为75﹪,那么一、二班的学生数各是多少?
根据题意,得方程组
x+y=100,
87.5﹪x+75﹪y=81﹪×100.
解得
x=48,
y=52.
答:一、二班的学生数分别为48名和52名.
解:设一、二班的学生分别为x名,y名.
鸡兔同笼,共有12个头,36只腿,则笼中有
只鸡, 只兔;
甲、乙两数之和是42,甲数的3倍等于乙数的4倍,求甲、乙两数各是多少?若设甲数为
x,乙数为y,依题意可列方程组 。
6
6
能力练习
3.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为( )
c
一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为( )
A、X=3,y=2 B、x=14,y=1
C、x=15,y=1 D、x=14,y=2
B
列二元一次方程组解决实际问题的一般步骤
(1)审题.
(2)设两个未知数,找两个等量关系.
(3)根据等量关系列方程,联立方程组.
(4)解方程组.
(5)检验并作答.
通过本课时的学习,我们需要掌握:
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
检 验
实际问题
的答案
巩固提高
练一练,相信你能行
某中学七年级(3)班51名同学为“希望工程”捐款,共捐款181元,捐款情况如下表,表格中捐款3元和4元的人数不小心被墨水污染已看不清楚.设捐款3元的有x名同学,捐款4元的有y名同学,
根据题意,可列方程组为:______________.
巩固提高
做一做
“五一期间”,你们一家5个大人和3个小孩去开心乐园,买门票共花了68元.我们家也是去开心乐园,不过比你家多2个大人,多1个小孩,门票共花了94元.如果我们家9个大人和5个小孩去开心乐园,买门票需要多少元呢?
设大人的门票每张为x元,小孩的门票每张为y元.列方程组得
努力提高自我
试一试 :某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由。
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=1680
2x+y=2280
解得:
x=960
y=360
(2)若7个餐厅同时开放,则有
5×960+2×360=5320
答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐。 (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐。
5320>5300
依题意得
想一想 :某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售。该公司的加工能力是:每天可以精加工6吨或粗加工16吨。现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?
解:设该公司应安排x天精加工,y天粗加工,
x+y=15
6x+16y=140
解 得:
x=10
y=5
答:该公司应安排x10天精加工,5天粗加工。
拓展延伸
依题意得
