人教版七年级数学下册 第八章 二元一次方程组8.2消元解二元一次方程组(第一课时)代入消元法 (共32张PPT)
文档属性
| 名称 | 人教版七年级数学下册 第八章 二元一次方程组8.2消元解二元一次方程组(第一课时)代入消元法 (共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 398.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:15:54 | ||
图片预览










文档简介
第八章 二元一次方程组
8.2 消元—解二元一次方程组
第1课时 代入法
本节学习目标 :
1、会用代入法解二元一次方程组。
2、初步体会解二元一次方程组的基本思 想——“消元”。
3、通过对方程中未知数特点的观察和分析,明确解二元一次方程组的主要思路是“消元”,从而促成未知向已知的转化,培养观察能力和体会化归的思想。
回顾与思考
含有两个未知数的一次方程叫做二元一次方程.
二元一次方程的概念:
由两个一次方程组成的含有两个未知数的方程组就叫做二元一次方程组.
二元一次方程组的概念:
3.已知y=2x-3,4x-3y=1时,x的值为 .
1. 把下列方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式?
(1)
(1)
(2)
y=2x-3
4
y=1-3x
1.把下列方程化成用含x的代数式表示y的形式.
①2x-y=6 ②3x-2y=4 ③5x+2y+1=0
练一练
解: ① y=2x-6
②
③
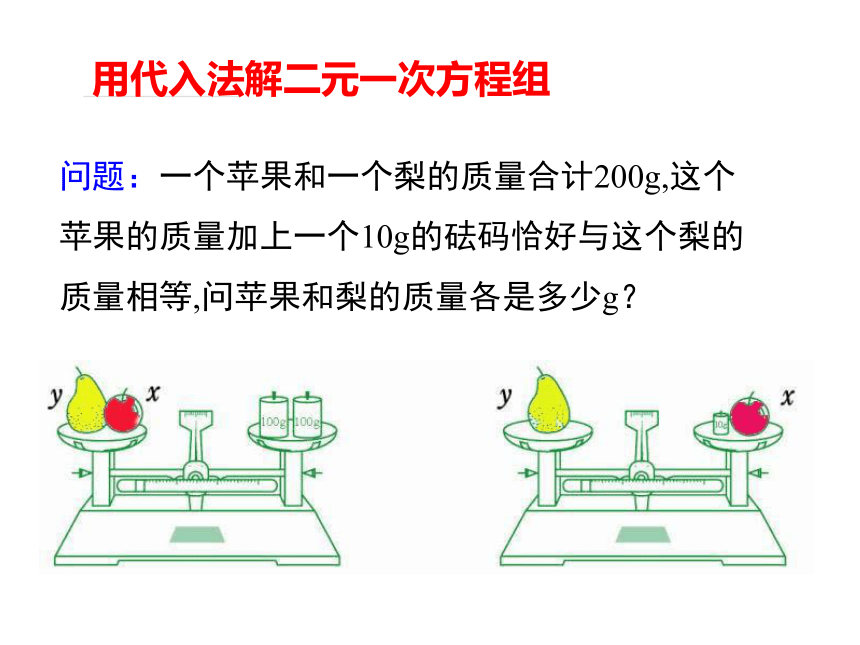
用代入法解二元一次方程组
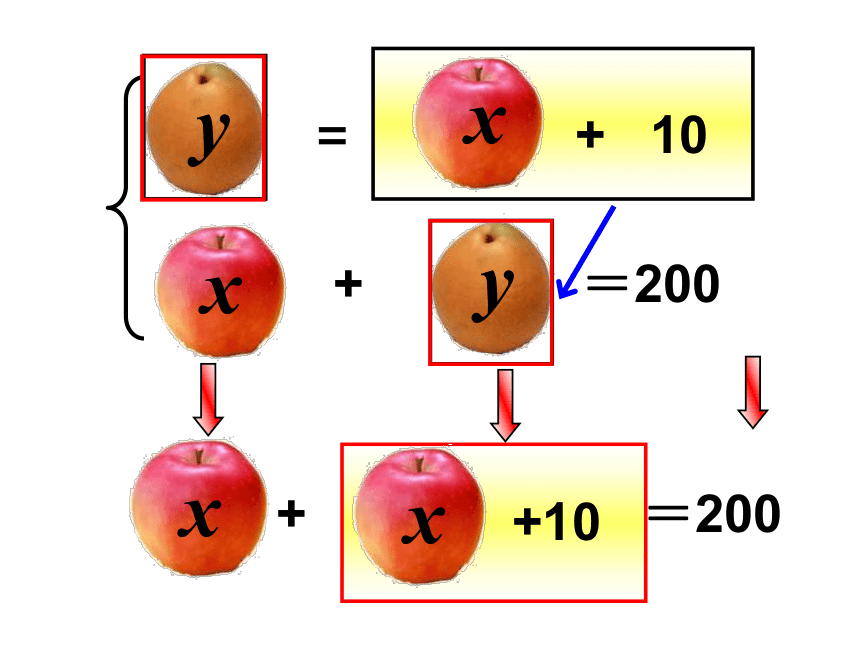
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
1.某班同学在植树节时植樟树和白杨树共45棵,已知樟树苗每棵2元,白杨树苗每棵1元,购买这些树苗用了60元.问樟树苗和白杨树苗各买了多少棵?
解 设樟树苗买了x棵,白杨树苗买了y棵,根据两种树苗总数为45,得
再根据购买树苗的总费用是60元,得
①
②
思考
解:设樟树x棵,则白杨树的棵数 (45–x)棵,根据题意,得:
2x+(45-x)=60
解方程,得
x=15
白杨树的棵数是45-x=45-15=30(棵)
y=45-x
代入
(或用含有y的代数式表示x);
将得到的一元一次方程的解代入原方程组中任意的一个方程(或代入变形后的方程)中,
将一个方程变形后代入另外一个方程中,
选择一个系数比较简单的方程,
(1)变形:
用含有x的代数式表示y
x + y =45
2x + y =60
①
②
(2)代入:
(3)解:
(4)反代:
(5)写出答案:
解:
由①,得
y=45-x
③
把③代入②,得
2x+(45-x)=60
解方程,得
x=15
把x=15代入③,得
y=30
x=15
y=30
消去一个未知数,得到一个一元一次方程;
解得到的一元一次方程;
求得另一个未知数数的值;
将方程组的解表示成 的形式.
x=a
y=b
所以这个方程组的解是
如何检验?
使二元一次方程组中每个方程都成立的两个未知数的值,叫做二元一次方程组的解.
二元一次方程组的解的定义
(二元一次方程组中两个方程的公共解)
3.方程组 的解是( )
练一练
B
1.二元一次方程组
的解是( )
A.
B.
C.
D.
D
当堂跟踪练习
x - y = 3 ,
3 x - 8 y = 14.
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
x = 2,
y =-1.
把y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x = y + 3 .③
注意:检验方程组的解
典例精析
例1 解方程组
解这个方程,得 y=-1.
思考:把③
代入①可以吗?
x –y = 3
3x -8 y = 14
练一练 解方程组
①
②
将得到的一元一次方程的解代入原方程组中任意的一个方程(或代入变形后的方程)中,
将一个方程变形后代入另外一个方程中,
选择一个系数比较简单的方程,
(1)变形:
用含有x的代数式表示y
(2)代入:
(3)解:
(4)反代:
(5)写出答案:
解:
由①,得
x = 3+ y
③
把③代入②,得
3(3+y)– 8y= 14
解方程,得
y= – 1
把y= – 1代入③,得
x =2
所以
x=2
y=– 1
消去一个未知数,得到一个一元一次方程;
解得到的一元一次方程;
求得另一个未知数数的值;
将方程组的解表示成 的形式.
x=a
y=b
(或用含有y的代数式表示x);
从一个方程中求出某一个未知数的表达式,
也就是要消去其中的一个未知数,
这里的消元方法是,
上面解二元一次方程组的基本思想是 ,
”消元”
把解二元一次方程组转化成解一元一次方程.
这种方法叫做代入消元法,简称代入法.
再把它“代入”另一个方程求解,
请同学们读一读:
用代入消元法解二元一次方程组的步骤:
(1)变形:选择一个系数比较简单的方程,用含有x的代数式表示y(或用含有y的代数式表示x);
(2)代入: 将一个方程变形后代入另外一个方程中,消去一个未知数,得到一个一元一次方程;
(3)解:解得到的一元一次方程;
(4)反代:将得到的一元一次方程的解代入原方程组中任意的一个方程(或代入变形后的方程)中,求得另一个未知数数的值;
(5)写出答案:将方程组的解表示成 的形式.
x=a
y=b
分析
解:由 得:x=3-2y
①
②
把 代入①得:
2(3-2y) +3y=-7
y = 13
把y = 13代入 得
x =3-2y=3-2×13=-23
∴
x = -23
y = 13
2 x +3y= -7
x = 3-2y
(3-2y)
谈谈思路
例2、解方程组
③
③
②
③
6-4y+3y=-7
-y=-13
③
主要步骤:
基本思路:
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
归纳反思
抢答: 请举手
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
2x+5y=21
x +3y=8
{
x-y=7y+9
5(x-y)=7-3y
1、用代入法求x和y的值
拓展探究:
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
x=1
y=-1
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
由题意知,
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
由①得:
y = 2 – 3x
把③代入得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y= 2 - 3×2
y= -4
∴
x = 2
y = -4
即x 的值是2,y 的值是-4.
所以原方程组的解:
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法:
例2 解方程组
解:
①
②
由①得:
x = 75-2y
③
把③代入②得:
2(75-2y)–y= 60
把y= 18代入③,得
x = 39
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
150-4y-y=60
– 5y= -90
y= 18
∴方程组的解是
x =39
y =18
说说方法
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴原方程组的解是
x=5
y=2
(在实践中学习)
由② ,得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
把y=2代入③ ,得 x=5
把③代入②可以吗?试试看
把y=2代入① 或②可以吗?
把求出的解代入原方程组,可以知道你解得对不对。
1.在解方程组 时可由x+y=6得到x=_____;
将其代入____中求出y=___.再将y 的值代入_____
中求出x=_____ .所以原方程组的解为
2.解方程组
能力检测
6-y
①
②
②
2
③
③
4
(1)
(2)
解方程组(3)
能力检测
①
②
你选择 哪个方程进行变形呢?
解得:
x=-7
y=13
x=-18
y=58
x=-6
y=7
(1)
(2)
(3)
你解对了吗!
4.李大叔去年承包了10亩地种植甲、乙两种蔬菜,共
获利18000元,其中甲种蔬菜每亩获利2000元,乙种
蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜
各种植了多少亩?
解: 设甲、乙两种蔬菜各种植了x亩、y亩,依题意得:
x+y=10, ①
2000x+1500y=18000. ②
由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
能力检测
主要步骤:
基本思路:
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
归纳反思
1
1
若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
根据已知条件可列方程组:
2m + n = 1
3m – 2n = 1
①
②
由①得:
把③代入②得:
n = 1 –2m
③
3m – 2(1 – 2m)= 1
3m – 2 + 4m = 1
7m = 3
把m 代入③,得:
知识拓展
1、二元一次方程组
这节课我们学习了
什么知识?
代入消元法
一元一次方程
2、代入消元法的一般步骤:
3、思想方法:转化思想、消元思想、
方程(组)思想.
知 识 梳 理
变
代
求
写
1
转化
8.2 消元—解二元一次方程组
第1课时 代入法
本节学习目标 :
1、会用代入法解二元一次方程组。
2、初步体会解二元一次方程组的基本思 想——“消元”。
3、通过对方程中未知数特点的观察和分析,明确解二元一次方程组的主要思路是“消元”,从而促成未知向已知的转化,培养观察能力和体会化归的思想。
回顾与思考
含有两个未知数的一次方程叫做二元一次方程.
二元一次方程的概念:
由两个一次方程组成的含有两个未知数的方程组就叫做二元一次方程组.
二元一次方程组的概念:
3.已知y=2x-3,4x-3y=1时,x的值为 .
1. 把下列方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式?
(1)
(1)
(2)
y=2x-3
4
y=1-3x
1.把下列方程化成用含x的代数式表示y的形式.
①2x-y=6 ②3x-2y=4 ③5x+2y+1=0
练一练
解: ① y=2x-6
②
③
用代入法解二元一次方程组
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
1.某班同学在植树节时植樟树和白杨树共45棵,已知樟树苗每棵2元,白杨树苗每棵1元,购买这些树苗用了60元.问樟树苗和白杨树苗各买了多少棵?
解 设樟树苗买了x棵,白杨树苗买了y棵,根据两种树苗总数为45,得
再根据购买树苗的总费用是60元,得
①
②
思考
解:设樟树x棵,则白杨树的棵数 (45–x)棵,根据题意,得:
2x+(45-x)=60
解方程,得
x=15
白杨树的棵数是45-x=45-15=30(棵)
y=45-x
代入
(或用含有y的代数式表示x);
将得到的一元一次方程的解代入原方程组中任意的一个方程(或代入变形后的方程)中,
将一个方程变形后代入另外一个方程中,
选择一个系数比较简单的方程,
(1)变形:
用含有x的代数式表示y
x + y =45
2x + y =60
①
②
(2)代入:
(3)解:
(4)反代:
(5)写出答案:
解:
由①,得
y=45-x
③
把③代入②,得
2x+(45-x)=60
解方程,得
x=15
把x=15代入③,得
y=30
x=15
y=30
消去一个未知数,得到一个一元一次方程;
解得到的一元一次方程;
求得另一个未知数数的值;
将方程组的解表示成 的形式.
x=a
y=b
所以这个方程组的解是
如何检验?
使二元一次方程组中每个方程都成立的两个未知数的值,叫做二元一次方程组的解.
二元一次方程组的解的定义
(二元一次方程组中两个方程的公共解)
3.方程组 的解是( )
练一练
B
1.二元一次方程组
的解是( )
A.
B.
C.
D.
D
当堂跟踪练习
x - y = 3 ,
3 x - 8 y = 14.
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
x = 2,
y =-1.
把y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x = y + 3 .③
注意:检验方程组的解
典例精析
例1 解方程组
解这个方程,得 y=-1.
思考:把③
代入①可以吗?
x –y = 3
3x -8 y = 14
练一练 解方程组
①
②
将得到的一元一次方程的解代入原方程组中任意的一个方程(或代入变形后的方程)中,
将一个方程变形后代入另外一个方程中,
选择一个系数比较简单的方程,
(1)变形:
用含有x的代数式表示y
(2)代入:
(3)解:
(4)反代:
(5)写出答案:
解:
由①,得
x = 3+ y
③
把③代入②,得
3(3+y)– 8y= 14
解方程,得
y= – 1
把y= – 1代入③,得
x =2
所以
x=2
y=– 1
消去一个未知数,得到一个一元一次方程;
解得到的一元一次方程;
求得另一个未知数数的值;
将方程组的解表示成 的形式.
x=a
y=b
(或用含有y的代数式表示x);
从一个方程中求出某一个未知数的表达式,
也就是要消去其中的一个未知数,
这里的消元方法是,
上面解二元一次方程组的基本思想是 ,
”消元”
把解二元一次方程组转化成解一元一次方程.
这种方法叫做代入消元法,简称代入法.
再把它“代入”另一个方程求解,
请同学们读一读:
用代入消元法解二元一次方程组的步骤:
(1)变形:选择一个系数比较简单的方程,用含有x的代数式表示y(或用含有y的代数式表示x);
(2)代入: 将一个方程变形后代入另外一个方程中,消去一个未知数,得到一个一元一次方程;
(3)解:解得到的一元一次方程;
(4)反代:将得到的一元一次方程的解代入原方程组中任意的一个方程(或代入变形后的方程)中,求得另一个未知数数的值;
(5)写出答案:将方程组的解表示成 的形式.
x=a
y=b
分析
解:由 得:x=3-2y
①
②
把 代入①得:
2(3-2y) +3y=-7
y = 13
把y = 13代入 得
x =3-2y=3-2×13=-23
∴
x = -23
y = 13
2 x +3y= -7
x = 3-2y
(3-2y)
谈谈思路
例2、解方程组
③
③
②
③
6-4y+3y=-7
-y=-13
③
主要步骤:
基本思路:
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
归纳反思
抢答: 请举手
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
2x+5y=21
x +3y=8
{
x-y=7y+9
5(x-y)=7-3y
1、用代入法求x和y的值
拓展探究:
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
x=1
y=-1
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
由题意知,
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
由①得:
y = 2 – 3x
把③代入得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y= 2 - 3×2
y= -4
∴
x = 2
y = -4
即x 的值是2,y 的值是-4.
所以原方程组的解:
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法:
例2 解方程组
解:
①
②
由①得:
x = 75-2y
③
把③代入②得:
2(75-2y)–y= 60
把y= 18代入③,得
x = 39
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
150-4y-y=60
– 5y= -90
y= 18
∴方程组的解是
x =39
y =18
说说方法
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴原方程组的解是
x=5
y=2
(在实践中学习)
由② ,得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
把y=2代入③ ,得 x=5
把③代入②可以吗?试试看
把y=2代入① 或②可以吗?
把求出的解代入原方程组,可以知道你解得对不对。
1.在解方程组 时可由x+y=6得到x=_____;
将其代入____中求出y=___.再将y 的值代入_____
中求出x=_____ .所以原方程组的解为
2.解方程组
能力检测
6-y
①
②
②
2
③
③
4
(1)
(2)
解方程组(3)
能力检测
①
②
你选择 哪个方程进行变形呢?
解得:
x=-7
y=13
x=-18
y=58
x=-6
y=7
(1)
(2)
(3)
你解对了吗!
4.李大叔去年承包了10亩地种植甲、乙两种蔬菜,共
获利18000元,其中甲种蔬菜每亩获利2000元,乙种
蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜
各种植了多少亩?
解: 设甲、乙两种蔬菜各种植了x亩、y亩,依题意得:
x+y=10, ①
2000x+1500y=18000. ②
由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
能力检测
主要步骤:
基本思路:
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
归纳反思
1
1
若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
根据已知条件可列方程组:
2m + n = 1
3m – 2n = 1
①
②
由①得:
把③代入②得:
n = 1 –2m
③
3m – 2(1 – 2m)= 1
3m – 2 + 4m = 1
7m = 3
把m 代入③,得:
知识拓展
1、二元一次方程组
这节课我们学习了
什么知识?
代入消元法
一元一次方程
2、代入消元法的一般步骤:
3、思想方法:转化思想、消元思想、
方程(组)思想.
知 识 梳 理
变
代
求
写
1
转化
