人教版数学七年级下册 7.2.2用坐标表示平移 (共30张PPT)
文档属性
| 名称 | 人教版数学七年级下册 7.2.2用坐标表示平移 (共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:27:32 | ||
图片预览








文档简介
1、什么叫做平移?
、平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
新图形中的每一点,都是由原图形中的某一点移动后得到的。
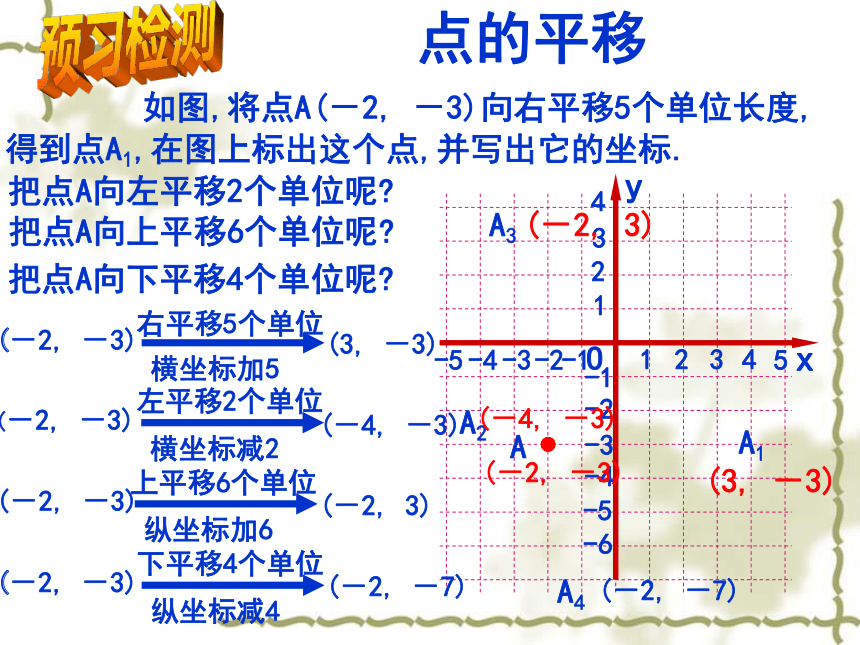
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢?
点的平移
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3, -3)
A
(-2, -3)
把点A向上平移6个单位呢?
A2
(-4, -3)
把点A向下平移4个单位呢?
A3
(-2, 3)
A4
(-2, -7)
(-2, -3)
右平移5个单位
(3, -3)
横坐标加5
(-2, -3)
左平移2个单位
(-4, -3)
横坐标减2
(-2, -3)
上平移6个单位
(-2, 3)
纵坐标加6
(-2, -3)
下平移4个单位
(-2, -7)
纵坐标减4
在平面直角坐标系中,
将点(x,y)向右平移a个单位长度,对应点的横坐标 a ,而纵坐标不变,即坐标变为 。
加上
将点(x,y)向左平移a个单位长度,对应点的横坐标 a ,而纵坐标不变,即坐标变为 。
(x+a,y)
(x-a,y)
减去
在平面直角坐标系中,
将点(x,y)向下平移a个单位长度,对应点的纵坐标 a ,而横坐标不变,即坐标变为 。
减去
将点(x,y)向上平移a个单位长度,对应点的纵坐标 a ,而横坐标不变,即坐标变为 。
(x,y-a)
(x,y+a)
加上
在平面直角坐标系中,有一点P(-4,2),
若将P:
(1)向左平移2个单位长度,所得点的坐标为______;
(2)向右平移3个单位长度,所得点的坐标为______;
(3)向下平移4个单位长度,所得点的坐标为______;
(4)向上平移3个单位长度,所得点的坐标为______;
(-6,2)
(-1,2)
(-4, -2)
(-4, 5)
1、如果A,B的坐标分别为A(-4,5),B(-4,2),将点A向___平移___个单位长度得到点B;将点B向___平移___个单位长度得到点A 。
2、如果P、Q的坐标分别为P(-3,-5),Q(2,-5),,将点P向___平移___个单位长度得到点Q;将点Q向___平移___个单位长度得到点P。
下
3
上
3
右
5
左
5
3.点A′(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)
向_________ _____得到B′(4,5)
向右平
移8个单位长度
上平移2个单位长度
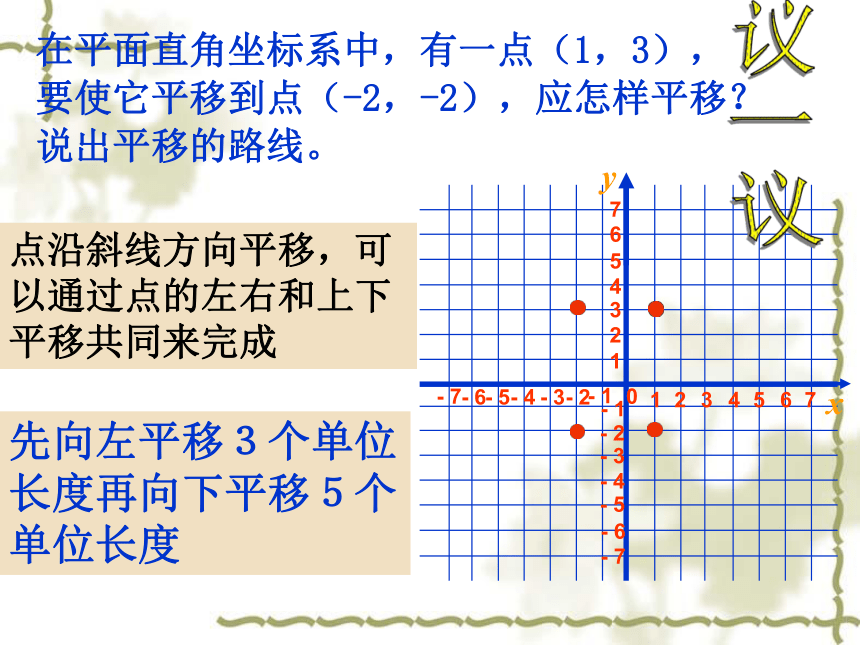
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线。
- 5
- 4
- 3
- 2
- 7
- 6
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
x
y
- 5
- 4
- 3
- 2
- 7
- 6
- 1
- 1
先向左平移3个单位长度再向下平移5个单位长度
点沿斜线方向平移,可以通过点的左右和上下平移共同来完成
1.把点M(1,2)平移后得到点N(1,-2)
则平移的过程是:
向下平移4个单位
2.把点M(-3,1)平移后得到点N(-1,4)
则平移的过程是:
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
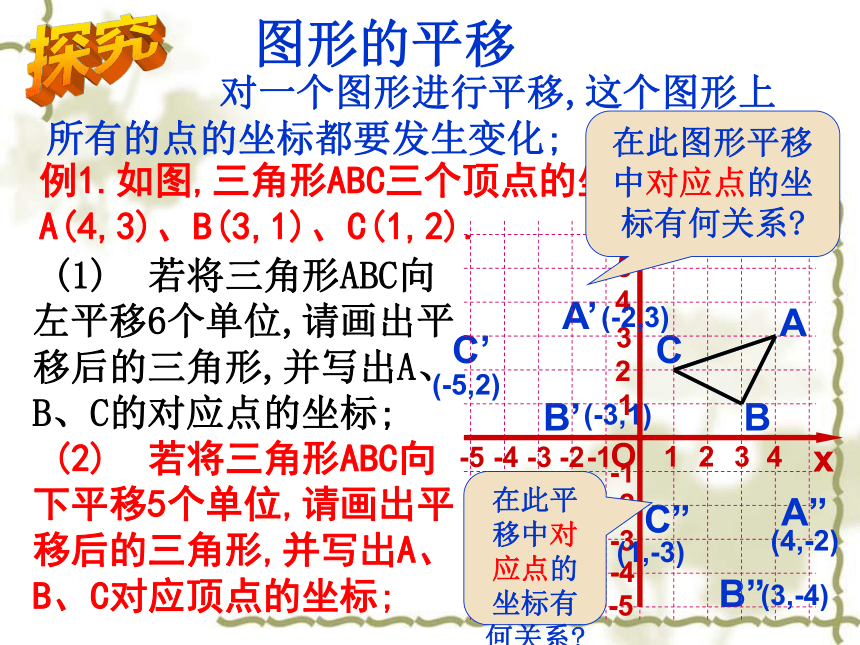
图形的平移
对一个图形进行平移,这个图形上所有的点的坐标都要发生变化;
例1.如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1) 若将三角形ABC向左平移6个单位,请画出平移后的三角形,并写出A、B、C的对应点的坐标;
A
B
C
A’
C’
B’
C”
B”
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
A”
(2) 若将三角形ABC向下平移5个单位,请画出平移后的三角形,并写出A、B、C对应顶点的坐标;
(-2,3)
(-3,1)
(-5,2)
(4,-2)
(3,-4)
(1,-3)
在此图形平移中对应点的坐标有何关系?
在此平移中对应点的坐标有何关系?
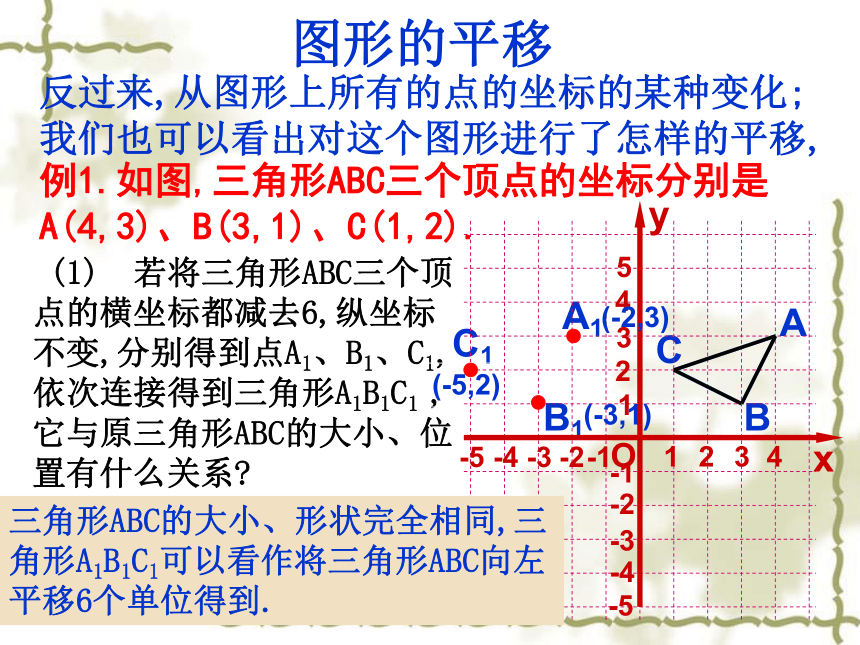
图形的平移
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移,
例1.如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1) 若将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接得到三角形A1B1C1 ,它与原三角形ABC的大小、位置有什么关系?
A
B
C
A1
C1
B1
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
(-2,3)
(-3,1)
(-5,2)
三角形ABC的大小、形状完全相同,三角形A1B1C1可以看作将三角形ABC向左平移6个单位得到.
图形的平移
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移,
例1.如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(2) 若将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接得到三角形A2B2C2,它与原三角形ABC的大小、位置有什么关系?
A
B
C
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
A2的纵坐标:3-5=-2
B2的纵坐标:1-5=-4
C2的纵坐标:2-5=-3
三角形ABC大小、形状完全相同,三角形A2B2C2可以看作将三角形ABC向下平移5个单位得到.
C2
B2
A2
(4,-2)
(3,-4)
(1,-3)
(1)横坐标变化,纵坐标不变
原图形向右平移a个单位
原图形上的点(x,y)
(x+a,y)
总结规律2:图形上点的坐标变化与图形平移间的关系
原图形向左平移a个单位
原图形上的点(x,y)
(x-a,y)
原图形向上平移b个单位
原图形上的点(x,y)
(x,y+b)
原图形向下平移b个单位
原图形上的点(x,y)
(x,y-b)
(2)横坐标不变,纵坐标变化:
(a>0)
(b>0)
将△ABC三个顶点的横坐标都减6,同时纵坐标减5,又能得到什么结论?
①
②
探究
总结:图形沿斜线方向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗?
1.将点A(-3,3)向左平移5个单位长度,
得到对应点坐标是
2.将点B(4,-5)向右平移3个单位长度,
得到对应点坐标是
3.将点C(-2,0)向上平移5个单位长度,
得到对应点坐标是
4.将点D(-1,3)向下平移5个单位长度,
得到对应点坐标是
(-8,3)
(7,-5)
(-2,5)
(-1,-2)
5.线段CD是由线段AB平移得到的,
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
6.观察下列图形,与图(1)的鱼相比,图(2)中的鱼发生了一些变化,若图(1)中鱼上P点的坐标为(4,3.2)则这个点在图(2)中的对应点P的坐标应为_______;
y
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
图1
图2
P
●
P
●
ⅹ
ⅹ
y
(4,2.2)
1.将点A(-3,2)向下平移3个单位,
再向右平移4个单位得点B,则B点坐
标是
2.将点P(0,-2)向左平移2个单位,
再向上平移4个单位得点Q(x,y),则
xy=
(1,-1)
-4
3.在平面直角坐标系中,有一点P(-4,2),若将P
先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_______。
(1,5)
4.在平面直角坐标系中,有一点P ,若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为( -3,9)。
(-8,6)
5.已知A(1,4),B(-4,0),C(2,0).
△ABC的面积是_____.
6.将△ABC向左平移三个单位后,点A、B、C的坐标分别变为______,______,____.
7.将△ABC向下平移三个单位后,点A、B、C的坐标分别变为______,______,____.
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
(-2,4)
(-7,0)
(-1,0)
(1,1)
(-4,-3)
(2,-3)
(1)
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(3)
0
(2)
小
结
(2)(3)中的三角形与(1)相比发生了哪些变化?
8.图中直角三角形的顶点坐标分别了什么变化?
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
9.如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),
将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
A(-2,3)
B(-4,-1)
C(2,0)
.
P(x0,y0)
.
P1(X0+5,y0+3)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
10、如图,小鱼的“嘴巴”所在的坐标是(1,1),小鱼沿x轴向左平移6个单位,此时,小鱼的“嘴巴”所在的坐标是多少?沿y轴向下平移4个单位呢?
通过这节课的学习你收获到哪些知识
这节的学习帮你解决了哪些问题?
通过这节课的学习你还有哪些问题?
1.将点P(m,1)向右平移5个单位长度,得
到点Q(3,1),则点P坐标为
(-2,1)
2.将点P(m+1,n -2)向上平移3个单位长
度,得到点Q(2,1- n),则点A(m,n)坐
标为
解:m +1=2 ,
n -2 +3 =1- n
故,m=1,n=0
所以,点A坐标为(1,0)
(1,0)
1.已知线段 MN=4,MN∥y轴,若点M坐标
为(-1,2),则N点坐标为
同类变式:
已知线段 MN=4,MN∥x轴,若点M坐标
为(-1,2),则N点坐标为
(-1,-2)或(-1,6)
(3,2)或(-5,2)
如图,一个机器人从O点出发,
向正东方向走3m到达A1点,再向正
北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点。按如此规律走下去,相对于点O,机器人走到A6点时是何位置?
解:以点O为原点,正东方向为x轴正方向,正北方向为y轴正方向,建立如答图所示的平面直角坐标系,题中机器人运动的过程,实质上是坐标系中点的平移过程,即A1(3,0)→A2(3,6)→A3(-6,6)→A4(-6,-6)→A5(9,-6)→A6(9,12).
?
A?
?
B?
?
C?
?
D?
A?(-3, -2) B?(1, -2) C?(2, 1) D?(-2, 1)
、平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
新图形中的每一点,都是由原图形中的某一点移动后得到的。
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢?
点的平移
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3, -3)
A
(-2, -3)
把点A向上平移6个单位呢?
A2
(-4, -3)
把点A向下平移4个单位呢?
A3
(-2, 3)
A4
(-2, -7)
(-2, -3)
右平移5个单位
(3, -3)
横坐标加5
(-2, -3)
左平移2个单位
(-4, -3)
横坐标减2
(-2, -3)
上平移6个单位
(-2, 3)
纵坐标加6
(-2, -3)
下平移4个单位
(-2, -7)
纵坐标减4
在平面直角坐标系中,
将点(x,y)向右平移a个单位长度,对应点的横坐标 a ,而纵坐标不变,即坐标变为 。
加上
将点(x,y)向左平移a个单位长度,对应点的横坐标 a ,而纵坐标不变,即坐标变为 。
(x+a,y)
(x-a,y)
减去
在平面直角坐标系中,
将点(x,y)向下平移a个单位长度,对应点的纵坐标 a ,而横坐标不变,即坐标变为 。
减去
将点(x,y)向上平移a个单位长度,对应点的纵坐标 a ,而横坐标不变,即坐标变为 。
(x,y-a)
(x,y+a)
加上
在平面直角坐标系中,有一点P(-4,2),
若将P:
(1)向左平移2个单位长度,所得点的坐标为______;
(2)向右平移3个单位长度,所得点的坐标为______;
(3)向下平移4个单位长度,所得点的坐标为______;
(4)向上平移3个单位长度,所得点的坐标为______;
(-6,2)
(-1,2)
(-4, -2)
(-4, 5)
1、如果A,B的坐标分别为A(-4,5),B(-4,2),将点A向___平移___个单位长度得到点B;将点B向___平移___个单位长度得到点A 。
2、如果P、Q的坐标分别为P(-3,-5),Q(2,-5),,将点P向___平移___个单位长度得到点Q;将点Q向___平移___个单位长度得到点P。
下
3
上
3
右
5
左
5
3.点A′(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)
向_________ _____得到B′(4,5)
向右平
移8个单位长度
上平移2个单位长度
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线。
- 5
- 4
- 3
- 2
- 7
- 6
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
x
y
- 5
- 4
- 3
- 2
- 7
- 6
- 1
- 1
先向左平移3个单位长度再向下平移5个单位长度
点沿斜线方向平移,可以通过点的左右和上下平移共同来完成
1.把点M(1,2)平移后得到点N(1,-2)
则平移的过程是:
向下平移4个单位
2.把点M(-3,1)平移后得到点N(-1,4)
则平移的过程是:
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
图形的平移
对一个图形进行平移,这个图形上所有的点的坐标都要发生变化;
例1.如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1) 若将三角形ABC向左平移6个单位,请画出平移后的三角形,并写出A、B、C的对应点的坐标;
A
B
C
A’
C’
B’
C”
B”
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
A”
(2) 若将三角形ABC向下平移5个单位,请画出平移后的三角形,并写出A、B、C对应顶点的坐标;
(-2,3)
(-3,1)
(-5,2)
(4,-2)
(3,-4)
(1,-3)
在此图形平移中对应点的坐标有何关系?
在此平移中对应点的坐标有何关系?
图形的平移
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移,
例1.如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1) 若将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接得到三角形A1B1C1 ,它与原三角形ABC的大小、位置有什么关系?
A
B
C
A1
C1
B1
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
(-2,3)
(-3,1)
(-5,2)
三角形ABC的大小、形状完全相同,三角形A1B1C1可以看作将三角形ABC向左平移6个单位得到.
图形的平移
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移,
例1.如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(2) 若将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接得到三角形A2B2C2,它与原三角形ABC的大小、位置有什么关系?
A
B
C
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
A2的纵坐标:3-5=-2
B2的纵坐标:1-5=-4
C2的纵坐标:2-5=-3
三角形ABC大小、形状完全相同,三角形A2B2C2可以看作将三角形ABC向下平移5个单位得到.
C2
B2
A2
(4,-2)
(3,-4)
(1,-3)
(1)横坐标变化,纵坐标不变
原图形向右平移a个单位
原图形上的点(x,y)
(x+a,y)
总结规律2:图形上点的坐标变化与图形平移间的关系
原图形向左平移a个单位
原图形上的点(x,y)
(x-a,y)
原图形向上平移b个单位
原图形上的点(x,y)
(x,y+b)
原图形向下平移b个单位
原图形上的点(x,y)
(x,y-b)
(2)横坐标不变,纵坐标变化:
(a>0)
(b>0)
将△ABC三个顶点的横坐标都减6,同时纵坐标减5,又能得到什么结论?
①
②
探究
总结:图形沿斜线方向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗?
1.将点A(-3,3)向左平移5个单位长度,
得到对应点坐标是
2.将点B(4,-5)向右平移3个单位长度,
得到对应点坐标是
3.将点C(-2,0)向上平移5个单位长度,
得到对应点坐标是
4.将点D(-1,3)向下平移5个单位长度,
得到对应点坐标是
(-8,3)
(7,-5)
(-2,5)
(-1,-2)
5.线段CD是由线段AB平移得到的,
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
6.观察下列图形,与图(1)的鱼相比,图(2)中的鱼发生了一些变化,若图(1)中鱼上P点的坐标为(4,3.2)则这个点在图(2)中的对应点P的坐标应为_______;
y
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
图1
图2
P
●
P
●
ⅹ
ⅹ
y
(4,2.2)
1.将点A(-3,2)向下平移3个单位,
再向右平移4个单位得点B,则B点坐
标是
2.将点P(0,-2)向左平移2个单位,
再向上平移4个单位得点Q(x,y),则
xy=
(1,-1)
-4
3.在平面直角坐标系中,有一点P(-4,2),若将P
先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_______。
(1,5)
4.在平面直角坐标系中,有一点P ,若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为( -3,9)。
(-8,6)
5.已知A(1,4),B(-4,0),C(2,0).
△ABC的面积是_____.
6.将△ABC向左平移三个单位后,点A、B、C的坐标分别变为______,______,____.
7.将△ABC向下平移三个单位后,点A、B、C的坐标分别变为______,______,____.
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
(-2,4)
(-7,0)
(-1,0)
(1,1)
(-4,-3)
(2,-3)
(1)
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(3)
0
(2)
小
结
(2)(3)中的三角形与(1)相比发生了哪些变化?
8.图中直角三角形的顶点坐标分别了什么变化?
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
9.如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),
将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
A(-2,3)
B(-4,-1)
C(2,0)
.
P(x0,y0)
.
P1(X0+5,y0+3)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
10、如图,小鱼的“嘴巴”所在的坐标是(1,1),小鱼沿x轴向左平移6个单位,此时,小鱼的“嘴巴”所在的坐标是多少?沿y轴向下平移4个单位呢?
通过这节课的学习你收获到哪些知识
这节的学习帮你解决了哪些问题?
通过这节课的学习你还有哪些问题?
1.将点P(m,1)向右平移5个单位长度,得
到点Q(3,1),则点P坐标为
(-2,1)
2.将点P(m+1,n -2)向上平移3个单位长
度,得到点Q(2,1- n),则点A(m,n)坐
标为
解:m +1=2 ,
n -2 +3 =1- n
故,m=1,n=0
所以,点A坐标为(1,0)
(1,0)
1.已知线段 MN=4,MN∥y轴,若点M坐标
为(-1,2),则N点坐标为
同类变式:
已知线段 MN=4,MN∥x轴,若点M坐标
为(-1,2),则N点坐标为
(-1,-2)或(-1,6)
(3,2)或(-5,2)
如图,一个机器人从O点出发,
向正东方向走3m到达A1点,再向正
北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点。按如此规律走下去,相对于点O,机器人走到A6点时是何位置?
解:以点O为原点,正东方向为x轴正方向,正北方向为y轴正方向,建立如答图所示的平面直角坐标系,题中机器人运动的过程,实质上是坐标系中点的平移过程,即A1(3,0)→A2(3,6)→A3(-6,6)→A4(-6,-6)→A5(9,-6)→A6(9,12).
?
A?
?
B?
?
C?
?
D?
A?(-3, -2) B?(1, -2) C?(2, 1) D?(-2, 1)
