人教版数学七年级下册第九章 9.2一元一次不等式(第1课时) (16张PPT)
文档属性
| 名称 | 人教版数学七年级下册第九章 9.2一元一次不等式(第1课时) (16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 195.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:41:37 | ||
图片预览






文档简介
9.2一元一次不等式
第1课时 一元一次不等式及其解法
学习目标
一元一次不等式
解一元一次不等式
一元一次不等式的特殊解
1
知识点
一元一次不等式
观察下列不等式:
x-7>26, 3x<2x+1, , -4x>3,
这些不等式有哪些共同特点?
思考:
1、只有一个未知数
2、未知数的指数是一次
3、不等号的两边都是整式
一元一次不等式
只含有一个未知数,并且未知数的最高次数为1,像这样的不等式,叫做一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
定义
下列式子中是一元一次不等式的有( )
(1)x2+1>2x;(2) +2>0;
(3)x>x-1; (4) ≤1.
A.1个 B.2个
C.3个 D.4个
√
A
2
知识点
解一元一次不等式
利用不等式的性质解一元一次不等式
x-7>26
x-7+7>26+7
移项
不等式性质1
解一元一次方程的基本步骤:
去分母
去括号
移项
合并同内项
系数化为1
解一元一次不等式的基本步骤
例1
去分母
去括号
移项
合并同内项
系数化为1
3(2+x) ≥ 2(2x-1)
6+3x ≥ 4x-2
3x-4x ≥ -2-6
-x ≥ -8
x ≤ 8
不等式两边同乘分母的最小公倍数
括号外的因数乘括号内的每一项
含未知数的项移到左边,常数项移到右边
根据合并同内项法则
不等式两边同除以未知数的系数
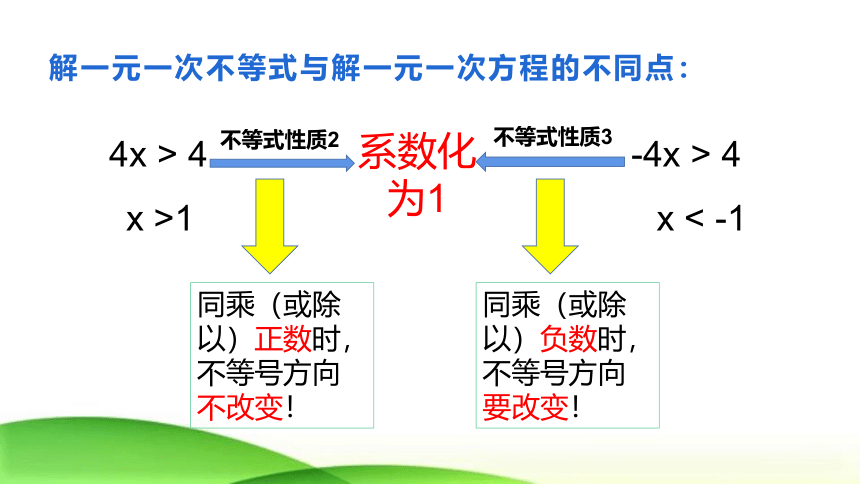
解一元一次不等式与解一元一次方程的不同点:
4x > 4
x >1
-4x > 4
x < -1
系数化为1
不等式性质2
同乘(或除以)正数时,不等号方向不改变!
不等式性质3
同乘(或除以)负数时,不等号方向要改变!
1、解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
练习
D
2、不等式3x+2<2x+3的解集在数轴上表示正确的是 ( )
D
3、解下列不等式,并在数轴上表示解集:
(1)
(2)
(1)去分母,得3(x-1)<7(2x+5),
去括号,得3x-3<14x+35,
移项,得3x-14x<35+3,
合并同类项,得-11x<38,
系数化为1,得x>-
这个不等式的解集在数轴上的表示:
0
-3
(2)去分母,得2(x+1)≥3(2x-5)+12,
去括号,得2x+2≥6x-15+12,
移项,合并同类项,得-4x≥-5,
系数化为1,得x ≤
这个不等式的解集在数轴上的表示:
0
1
解:
3
知识点
一元一次不等式的特殊解
求不等式3(x+1)≥5x-9的非负整数解.
例2:
①求出原不等式的解集
②找出解集内包含的“非负整数解”(0和正整数解)
解:
解不等式3(x+1)≥5x-9得:
x≤6.
∴不等式3(x+1)≥5x-9的非负整数解为:
0,1,2,3,4,5,6.
关于x的方程 3x-3k=5(x-k)+6的解是负数,求k的取值范围。
①求出原方程的解(用含有k的式子来表示x);
②解为负数,即x<0,再解不等式,求出K的取值范围。
例3:
解:
由题意得:x=k-3
∵x为负数
∴k-3<0
即:k<3
练习
已知不等式5x-2<6x+1的最小正整数解是方程 的解,求a的值。
①求出原不等式的解集;
②找出解集里的最小正整数解;
③把最小正整数解代入方程中,求出a的值。
解不等式得:x>-3.
∴不等式5x-2<6x+1的最小正整数解为:x=1
把x=1代入方程 中,得:
a=-2
解:
1、若x=2是不等式2x-a-2<0的一个解,则a可取的最小正整数为( )
A.2 ????B.3 ????C.4 ????D.5
答案????B ∵x=2是不等式的一个解,
∴将x=2代入不等式,得4-a-2<0,解得a>2,
∴a可取的最小正整数为3。
2、若关于x的方程2x+1=3k的解是负数,则k的取值范围为 ????.
答案 k< 解2x+1=3k,得x= ?,
根据题意得?<0,
解得k< ?
B
总结
1、一元一次不等式的判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
2. 解一元一次不等式的一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1.
课后作业
课本126页(习题9.2):
第1题的(3)和(6);(注意用数轴表示)
第2题;
第3题的(2)和(4)。
再见!
第1课时 一元一次不等式及其解法
学习目标
一元一次不等式
解一元一次不等式
一元一次不等式的特殊解
1
知识点
一元一次不等式
观察下列不等式:
x-7>26, 3x<2x+1, , -4x>3,
这些不等式有哪些共同特点?
思考:
1、只有一个未知数
2、未知数的指数是一次
3、不等号的两边都是整式
一元一次不等式
只含有一个未知数,并且未知数的最高次数为1,像这样的不等式,叫做一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
定义
下列式子中是一元一次不等式的有( )
(1)x2+1>2x;(2) +2>0;
(3)x>x-1; (4) ≤1.
A.1个 B.2个
C.3个 D.4个
√
A
2
知识点
解一元一次不等式
利用不等式的性质解一元一次不等式
x-7>26
x-7+7>26+7
移项
不等式性质1
解一元一次方程的基本步骤:
去分母
去括号
移项
合并同内项
系数化为1
解一元一次不等式的基本步骤
例1
去分母
去括号
移项
合并同内项
系数化为1
3(2+x) ≥ 2(2x-1)
6+3x ≥ 4x-2
3x-4x ≥ -2-6
-x ≥ -8
x ≤ 8
不等式两边同乘分母的最小公倍数
括号外的因数乘括号内的每一项
含未知数的项移到左边,常数项移到右边
根据合并同内项法则
不等式两边同除以未知数的系数
解一元一次不等式与解一元一次方程的不同点:
4x > 4
x >1
-4x > 4
x < -1
系数化为1
不等式性质2
同乘(或除以)正数时,不等号方向不改变!
不等式性质3
同乘(或除以)负数时,不等号方向要改变!
1、解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
练习
D
2、不等式3x+2<2x+3的解集在数轴上表示正确的是 ( )
D
3、解下列不等式,并在数轴上表示解集:
(1)
(2)
(1)去分母,得3(x-1)<7(2x+5),
去括号,得3x-3<14x+35,
移项,得3x-14x<35+3,
合并同类项,得-11x<38,
系数化为1,得x>-
这个不等式的解集在数轴上的表示:
0
-3
(2)去分母,得2(x+1)≥3(2x-5)+12,
去括号,得2x+2≥6x-15+12,
移项,合并同类项,得-4x≥-5,
系数化为1,得x ≤
这个不等式的解集在数轴上的表示:
0
1
解:
3
知识点
一元一次不等式的特殊解
求不等式3(x+1)≥5x-9的非负整数解.
例2:
①求出原不等式的解集
②找出解集内包含的“非负整数解”(0和正整数解)
解:
解不等式3(x+1)≥5x-9得:
x≤6.
∴不等式3(x+1)≥5x-9的非负整数解为:
0,1,2,3,4,5,6.
关于x的方程 3x-3k=5(x-k)+6的解是负数,求k的取值范围。
①求出原方程的解(用含有k的式子来表示x);
②解为负数,即x<0,再解不等式,求出K的取值范围。
例3:
解:
由题意得:x=k-3
∵x为负数
∴k-3<0
即:k<3
练习
已知不等式5x-2<6x+1的最小正整数解是方程 的解,求a的值。
①求出原不等式的解集;
②找出解集里的最小正整数解;
③把最小正整数解代入方程中,求出a的值。
解不等式得:x>-3.
∴不等式5x-2<6x+1的最小正整数解为:x=1
把x=1代入方程 中,得:
a=-2
解:
1、若x=2是不等式2x-a-2<0的一个解,则a可取的最小正整数为( )
A.2 ????B.3 ????C.4 ????D.5
答案????B ∵x=2是不等式的一个解,
∴将x=2代入不等式,得4-a-2<0,解得a>2,
∴a可取的最小正整数为3。
2、若关于x的方程2x+1=3k的解是负数,则k的取值范围为 ????.
答案 k< 解2x+1=3k,得x= ?,
根据题意得?<0,
解得k< ?
B
总结
1、一元一次不等式的判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
2. 解一元一次不等式的一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1.
课后作业
课本126页(习题9.2):
第1题的(3)和(6);(注意用数轴表示)
第2题;
第3题的(2)和(4)。
再见!
