人教版数学七下8.2.1代入消元法解二元一次方程组课件(26张PPT)
文档属性
| 名称 | 人教版数学七下8.2.1代入消元法解二元一次方程组课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 303.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:24:28 | ||
图片预览








文档简介
8.2.1代入消元法解二元一次方程组(2)
本节学习目标 :
1、会用代入法解二元一次方程组.
2、初步体会解二元一次方程组的基本思想——“消元”.
3、通过对方程中未知数特点的观察和分析,明确解二元一次方程组的主要思路是“消元”,从而促成未知向已知的转化,培养观察能力和体会化归的思想.
1、解二元一次方程组的基本思想是什么?
2、代入消元法解二元一次方程组的一般步骤:
消元,即将二个未知数化为一个未知数
(1)变形;(2)代入;(3)求解;(4)回代;(5)写解
一、复习回顾
3、解方程组
x+y=7 ①
3x+y=17 ②
例2 根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)的比为 .某厂每天生产这种消毒液 22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
二、探索新知
问题1、此方程于我们前面遇到的方程有什么不同?
两个方程中两个未知数的绝对值都不为1
问题2、能用代入法求解吗?
问题3、选择哪个方程进行变形?消去哪个未知数?
解:设这些消毒液应该分装x大瓶、y小瓶.
由题意得
③
解得 x=20000
把x=20000代入③,得 y=50000
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
?
í
ì
=
+
=
22500000
250
500
2
5
y
x
y
x
把③代入②,得
由①,得
解:设这些消毒液应该分装x大瓶、y小瓶.
由题意得
.
题目中包含的两个等量关系:
分析:
(1)大瓶数:小瓶数=2:5
(2)大瓶所装消毒液+小平所装消毒液=总生产量
解:把①代入②, 得
100×2y+250y=22500000
解得 y=50000
整体代入法
①
②
把y=50000代入① ,得 x=20000
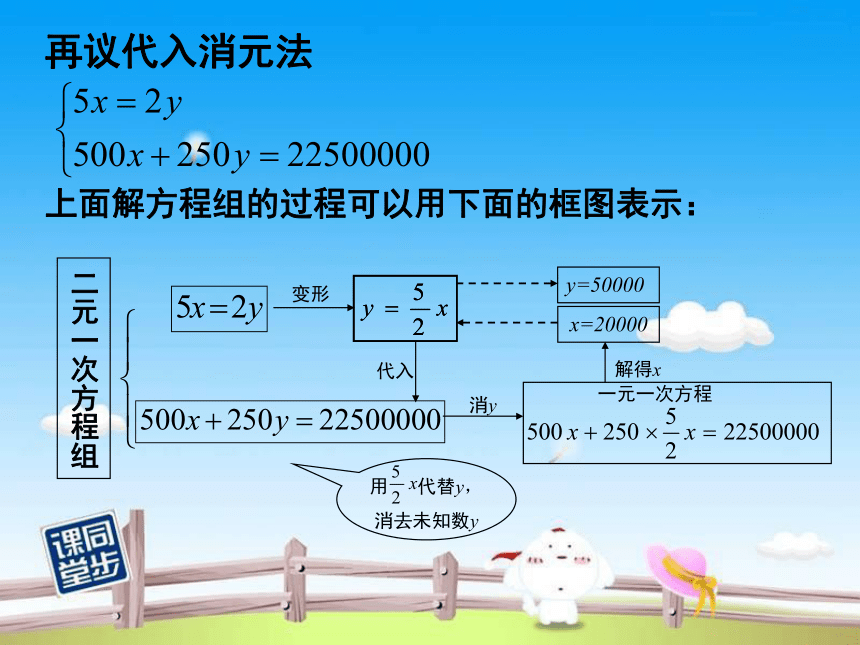
二元一次方程组
变形
代入
y=50000
x=20000
解得x
一元一次方程
消y
用 代替y,
消去未知数y
上面解方程组的过程可以用下面的框图表示:
再议代入消元法
代入消元法的一般步骤
(1)变形:将其中一个方程的某个未知数用含有另一个未知数的代数式表示(即y=ax+b或x=my+n)
(2)代入:将变形后的方程代入另一个方程中,消去一个未知数,化二元一次方程组为一元一次方程.
(3)求解:解一元一次方程,得一个未知数的值.
(4)回代:将求得的未知数的值代入到变形后的方程中求出另一个未知数的值.
(5)写解:用 的形式写出方程组的解.
解二元一次方程组的基本思想
——“消元”。
巩固与提高:
2x-y=-5
⑴
4x+3y=65
⑵
5x+6y=13
7x+18y=-1
⑶
5x-2y=-1
⑷
3x-9=2y
4x+2y=12
1、用代入消元法解下列方程组
(1)
4x+3y=65 ②
2x-y=-5 ①
解:由①,得 y = 2x + 5 ③
把③代入②,得 4 x+3(2x + 5 )=65
解得 x=5
把x=5代入③,得 y=15
∴原方程组的解是
5x+6y=13 ①
⑵
7x+18y=-1 ②
解:由①,得6y=13-5x ③
把③代入②得,7x+3(13-5x)=-1
解得 x=5
把x=5代入③得, y=-2
所以,原方程组的解是
①
(3)
②
5x-2y=-1
解:由①,得 3(x+3)=2(y+1)
3x+9=2y+2
3x+7=2y ③
把③代入② ,得 5x-(3x+7)=-1
x=3
把x=3代入③ ,得 y=8
∴原方程组的解是
解:令 = k,则x=2k-3,③y=3k-1,④
把③、④代入②,得5(2k-3)-2(3k-1)=-1
解得 k=3
把k=3代入③、④,得 X=3,y=8
∴原方程组的解是
3x-9=2y ①
4x+2y=12 ②
(4)
解:把①代入② ,得 4x+(3x-9)=12
4x+3x-9=12
解得 x=3
把x=3代入① ,得 y=0
∴原方程组的解是
1
1
2、若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
由条件可得:
2m + n = 1
3m – 2n = 1
①
②
由①,得 n = 1 –2m ③
3m – 2(1 – 2m)= 1
3m – 2 + 4m = 1
7m = 3
把m 代入③,得
把③代入②,得
3.已知 的解
是 ,求a,b的值.
解:根据题意可列方程组
①
②
由① ,得 .③
把③代入② ,得 4b+ =2.
得 b=-1.
把b=-1代入③ ,得 a=2.
∴a=2,b=-1.
16b+3(5-3b)=8
16b+15-9b=8
7b=-7
b=-1
解:根据题意可列方程组
①
②
由①+② ,得 7a+7b=7 , a+b=1 .
把③代入② ,得 4b+ 3(1-b)=2.
得 b=-1.
把b=-1代入③ ,得 a=2.
∴a=2,b=-1.
b=1 -a . ③
4b+3-3b=2.
5.为了保护环境,某校环保小组成员收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克;第二天收集1号电池2节,5号电池3节,总重量为240克.试问1号电池和5号电池每节分别重多少克?
解:设1号电池每节重x克,5号电池每节重y克.
根据题意可列方程组:
①
②
①
②
由②, 得 2x=240-3y ③
把③代入①,得 2(240-3y)+5y=460
480-6y+5y=460
-y=-20
y=20.
把y=20代入③,得 2x+3×20=240
x=90.
解:设1号电池每节重x克,5号电池每节重y克.
根据题意可列方程组:
①
②
答:1号电池每节重90克,5号电池每节重20克.
代入消元法的一般步骤
(1)变形:将其中一个方程的某个未知数用含有另一个未知数的代数式表示(即y=ax+b或x=my+n)
(2)代入:将变形后的方程代入另一个方程中,消去一个未知数,化二元一次方程组为一元一次方程.
(3)求解:解一元一次方程,得一个未知数的值.
(4)回代:将求得的未知数的值代入到变形后的方程中求出另一个未知数的值.
(5)写解:用 的形式写出方程组的解.
解二元一次方程组的基本思想
——“消元”。
作业:
1、必做题:课本习题8.2 第2题
2、选做题:
二元一次方程组 的解
x和y相等,则k = .
本节学习目标 :
1、会用代入法解二元一次方程组.
2、初步体会解二元一次方程组的基本思想——“消元”.
3、通过对方程中未知数特点的观察和分析,明确解二元一次方程组的主要思路是“消元”,从而促成未知向已知的转化,培养观察能力和体会化归的思想.
1、解二元一次方程组的基本思想是什么?
2、代入消元法解二元一次方程组的一般步骤:
消元,即将二个未知数化为一个未知数
(1)变形;(2)代入;(3)求解;(4)回代;(5)写解
一、复习回顾
3、解方程组
x+y=7 ①
3x+y=17 ②
例2 根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)的比为 .某厂每天生产这种消毒液 22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
二、探索新知
问题1、此方程于我们前面遇到的方程有什么不同?
两个方程中两个未知数的绝对值都不为1
问题2、能用代入法求解吗?
问题3、选择哪个方程进行变形?消去哪个未知数?
解:设这些消毒液应该分装x大瓶、y小瓶.
由题意得
③
解得 x=20000
把x=20000代入③,得 y=50000
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
?
í
ì
=
+
=
22500000
250
500
2
5
y
x
y
x
把③代入②,得
由①,得
解:设这些消毒液应该分装x大瓶、y小瓶.
由题意得
.
题目中包含的两个等量关系:
分析:
(1)大瓶数:小瓶数=2:5
(2)大瓶所装消毒液+小平所装消毒液=总生产量
解:把①代入②, 得
100×2y+250y=22500000
解得 y=50000
整体代入法
①
②
把y=50000代入① ,得 x=20000
二元一次方程组
变形
代入
y=50000
x=20000
解得x
一元一次方程
消y
用 代替y,
消去未知数y
上面解方程组的过程可以用下面的框图表示:
再议代入消元法
代入消元法的一般步骤
(1)变形:将其中一个方程的某个未知数用含有另一个未知数的代数式表示(即y=ax+b或x=my+n)
(2)代入:将变形后的方程代入另一个方程中,消去一个未知数,化二元一次方程组为一元一次方程.
(3)求解:解一元一次方程,得一个未知数的值.
(4)回代:将求得的未知数的值代入到变形后的方程中求出另一个未知数的值.
(5)写解:用 的形式写出方程组的解.
解二元一次方程组的基本思想
——“消元”。
巩固与提高:
2x-y=-5
⑴
4x+3y=65
⑵
5x+6y=13
7x+18y=-1
⑶
5x-2y=-1
⑷
3x-9=2y
4x+2y=12
1、用代入消元法解下列方程组
(1)
4x+3y=65 ②
2x-y=-5 ①
解:由①,得 y = 2x + 5 ③
把③代入②,得 4 x+3(2x + 5 )=65
解得 x=5
把x=5代入③,得 y=15
∴原方程组的解是
5x+6y=13 ①
⑵
7x+18y=-1 ②
解:由①,得6y=13-5x ③
把③代入②得,7x+3(13-5x)=-1
解得 x=5
把x=5代入③得, y=-2
所以,原方程组的解是
①
(3)
②
5x-2y=-1
解:由①,得 3(x+3)=2(y+1)
3x+9=2y+2
3x+7=2y ③
把③代入② ,得 5x-(3x+7)=-1
x=3
把x=3代入③ ,得 y=8
∴原方程组的解是
解:令 = k,则x=2k-3,③y=3k-1,④
把③、④代入②,得5(2k-3)-2(3k-1)=-1
解得 k=3
把k=3代入③、④,得 X=3,y=8
∴原方程组的解是
3x-9=2y ①
4x+2y=12 ②
(4)
解:把①代入② ,得 4x+(3x-9)=12
4x+3x-9=12
解得 x=3
把x=3代入① ,得 y=0
∴原方程组的解是
1
1
2、若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
由条件可得:
2m + n = 1
3m – 2n = 1
①
②
由①,得 n = 1 –2m ③
3m – 2(1 – 2m)= 1
3m – 2 + 4m = 1
7m = 3
把m 代入③,得
把③代入②,得
3.已知 的解
是 ,求a,b的值.
解:根据题意可列方程组
①
②
由① ,得 .③
把③代入② ,得 4b+ =2.
得 b=-1.
把b=-1代入③ ,得 a=2.
∴a=2,b=-1.
16b+3(5-3b)=8
16b+15-9b=8
7b=-7
b=-1
解:根据题意可列方程组
①
②
由①+② ,得 7a+7b=7 , a+b=1 .
把③代入② ,得 4b+ 3(1-b)=2.
得 b=-1.
把b=-1代入③ ,得 a=2.
∴a=2,b=-1.
b=1 -a . ③
4b+3-3b=2.
5.为了保护环境,某校环保小组成员收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克;第二天收集1号电池2节,5号电池3节,总重量为240克.试问1号电池和5号电池每节分别重多少克?
解:设1号电池每节重x克,5号电池每节重y克.
根据题意可列方程组:
①
②
①
②
由②, 得 2x=240-3y ③
把③代入①,得 2(240-3y)+5y=460
480-6y+5y=460
-y=-20
y=20.
把y=20代入③,得 2x+3×20=240
x=90.
解:设1号电池每节重x克,5号电池每节重y克.
根据题意可列方程组:
①
②
答:1号电池每节重90克,5号电池每节重20克.
代入消元法的一般步骤
(1)变形:将其中一个方程的某个未知数用含有另一个未知数的代数式表示(即y=ax+b或x=my+n)
(2)代入:将变形后的方程代入另一个方程中,消去一个未知数,化二元一次方程组为一元一次方程.
(3)求解:解一元一次方程,得一个未知数的值.
(4)回代:将求得的未知数的值代入到变形后的方程中求出另一个未知数的值.
(5)写解:用 的形式写出方程组的解.
解二元一次方程组的基本思想
——“消元”。
作业:
1、必做题:课本习题8.2 第2题
2、选做题:
二元一次方程组 的解
x和y相等,则k = .
