华东师大版七上数学 4.6.2角的比较和运算 教案
文档属性
| 名称 | 华东师大版七上数学 4.6.2角的比较和运算 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 06:56:27 | ||
图片预览

文档简介
《4.3.2 角的比较与运算》教学设计
一、教学目标
1、会比较两个角的大小,在操作中理解角平分线的意义。
2、通过三角尺特殊角的拼画,深刻地理解角的和、差,并会进行角度的初步运算。
3、引导学生在观察、交流、实践等活动的基础上,逐渐培养动手操作能力、几何语言的表达能力以及几何识图能力,提高数学活动的经验。
4、在充分的活动体验中,让学生快乐有效地学习。
二、教学重点:角的比较,角的和、差运算。
三、教学难点:角平分线的应用及几何语言的书写。
四、教学方法:
类比思想:比线段,与比角的类比教学(从探究到书写应用)。
动手实践:角的纸板模型比较、三角板的拼画角度、角分线的作法等教学实践环节,给学生提供了充分的活动空间,体现了“做中学”的教学理念。
小组合作:教学中的几个探究活动,充分体现了小组合作的团结协作的力量,同学们的互助学习,不仅能提高学习的能力,还能增加之间的友谊,进一步促进了学习的欲望。
课件辅助:在课件演示中能生动形象地展现出“比”所体现出的方法与要领。
五、教学准备:一副三角板,几个纸板角,量角器,多媒体制作的ppt课件等。
六、教学过程:
教学环节 教 学 呈 现 教 学 意 图
一、
情景引入 引言:线段和角是几何中最基本的两个图形,线的知识我们已初步学习过了,今天进一步学习角的知识。
师:板书课题,并指出学习目标。
师:拿出如图两个角,请同学们说说,这两角谁大谁小?
学生可能有说: 红的角大,因为它的边长(或者它的整体看着大)。
也可能会说: 好像一样大,角的大小不能看边,看角度。
同学们会在各种观点中,得到启示,并开始琢磨深思。
老师适时引导:什么是角?角的两边是什么?
生:是两条射线,噢,两边是无限延伸的。
师:对,角的两边是无限延伸的,这两个角只是其中的一部分。因此角的大小比较是指度数的大小比较,与边的长短无关。 从“形”上看,度数越大,开口也越大。 通过比较边长不等的两个角的大小引入,激起学生思维火花的碰撞,老师的适时点拨,引发学生对角的定义的再次认识,得出角的比较是看角度的大小,而不是边的长短这一误区,更深刻地理解角的知识。
从“数”与“形”两方面来认识角。
二、
探知
角的比较 一、知识回顾
师:我们是怎样比较两条线段的长短?
生:各抒己见(摆在一起比,或测量长度)
师:播放两条线段比较的动画演示。
生:随着情境,用语言表达点的位置。
师:那么,怎样比较两个角的大小呢?
多媒体的动态展示,更能形象生动地体现“比”的过程。运用类比思想,为新知作铺垫。
二、活动探究
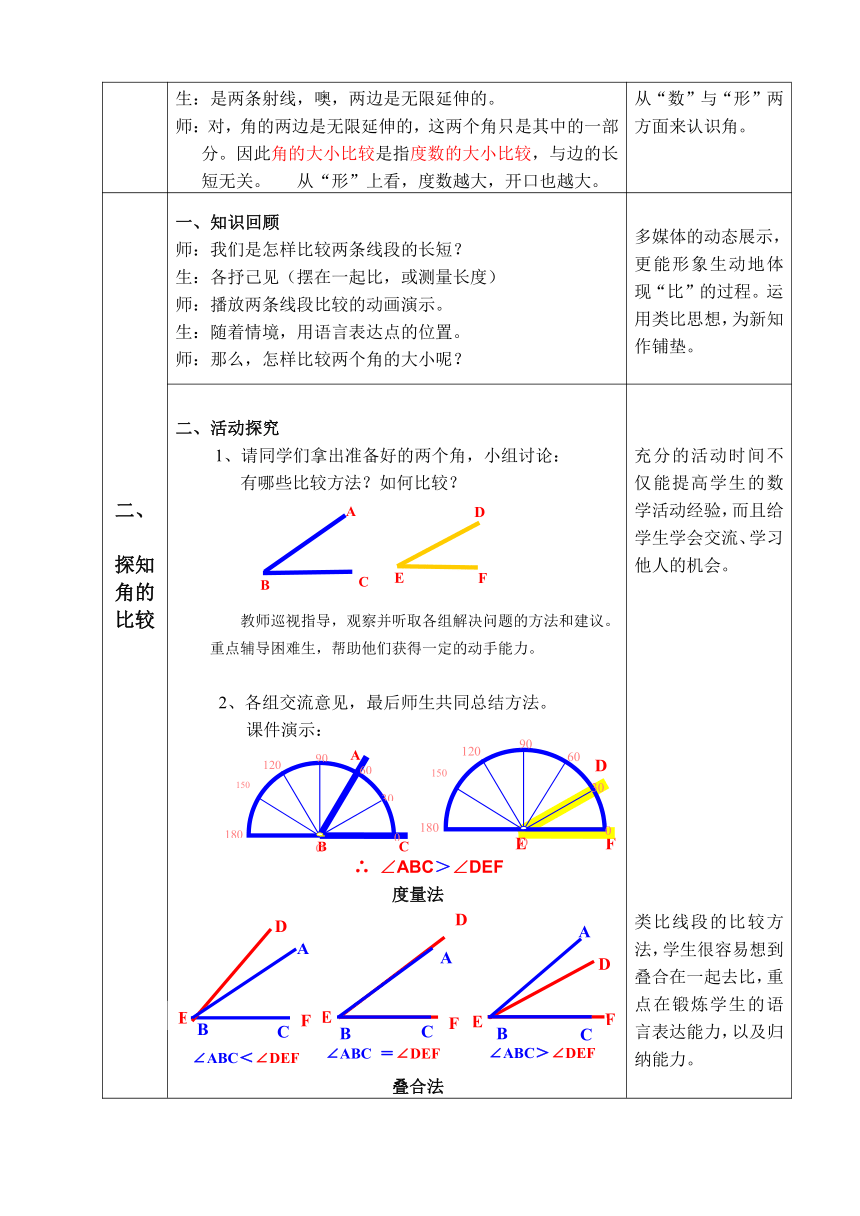
1、请同学们拿出准备好的两个角,小组讨论:
有哪些比较方法?如何比较?
教师巡视指导,观察并听取各组解决问题的方法和建议。重点辅导困难生,帮助他们获得一定的动手能力。
2、各组交流意见,最后师生共同总结方法。
课件演示:
度量法
叠合法
充分的活动时间不仅能提高学生的数学活动经验,而且给学生学会交流、学习他人的机会。
类比线段的比较方法,学生很容易想到叠合在一起去比,重点在锻炼学生的语言表达能力,以及归纳能力。
三、
探知角的运算 一、探求角的和与差:
1、给出问题:图中共有几个角?
它们之间有什么数量关系?
学生口答。
学生得出的关系可能很多,可能
会有大小关系,老师应总结出三个角
之间的和差关系。
2、练一练:口答。
∠AOD=∠AOC+__________
∠AOB=∠AOD-__________
∠BOC=∠BOD-__________
若∠AOB=∠COD,那么图中
还有两个相等的角是___________。
3、算一算。
例1 如图,∠AOB是直角,
∠BOC=34?,
求∠AOC的度数。
请一学生说说思路,
老师板书示范,要求推理格式。
学生模拟演算。
例2 如图,O是直线AB上一点,
∠AOC=53?17'。
求∠BOC的度数。
请一学生分析已知条件,说说思路。
老师板书示范,要求推理格式。
学生在理解的基础上模拟演算。感悟几何推理的逻辑性。 承上启下,有角的比较,又为角的和、差关系提供问题情境。
体现知识的关联与生长。
把形与度数的表示结合起来。
在众多角中辨清角,充实了知识。
第四问是训练学生的等量角的和的运算,是今后角度推理的重点。
例1的增加是为了示范角度求解的书写格式。
注意平角的推理,以及单位运算。
引导学生要会看已知条件,挖掘条件,并把已知标图上。
两道例题的设置,是为巩固和深化角的和、差的知识运算。从“数”与“形”两个角度进一步认识角。
二、活动探究
1、借助手中的一副三角板,你能拼出15?, 75?, 105°的角吗?你还可以拼出其他角吗?
小组探究,画出各种情况。
老师巡视指导,关注学困生使用三角板的熟练程度。
2、请学生在黑板上作画,老师帮助指导三角板的使用。
在活动中加强工具的熟练度,提高学生学习乐趣,使学生在“做中学”中深刻体会角的和与差。
小组活动,培养团结互助的良好品质。
四、
新知学习
五、
练习
应用
一、角平分线定义
师:线段的中点将线段分成相等的两部分,角有类似的现象吗?
生:仔细观察图形,并发表自己的观点。
师生共同总结:从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。
几何语言:
∵射线OB是∠AOC的角平分线,
∴∠AOB=∠BOC= ∠AOC
或∠AOC=2∠BOC = 2∠AOB
学生作笔记,感悟因果推理的表达。
类似地,还有角的三等分线:
仿照角分线让学生表达几何语言。
二、角分线作法
师:请同学们拿出你准备的一个角,如何画出它的角分线?
生:或独立完成,或同桌交流。
老师巡视观察,适当点拨设问。
请同学们展示归纳方法:折叠,折痕即为角分线。
测量,平分度数。
师:我们目前作角分线的方法,这两种即可以,只是在测量时,约平分度数即可,如何更精确地平分度数,下节课继续学。
1、如图所示,射线OE平分∠BOC,射线OD平分 ∠AOC,∠BOE=20°∠AOD=40°,求∠AOB的度数。
师:带着学生将角度标在图上。
先独立完成,要有推理过程。
再将你的书写过程与小组交流。
生:两名学生上黑板板演。
师生共同分析,注重推理及书写的格式要求。
老师启发学生思考,培养学生的分析能力。
几何语言的训练要重视,这是培养学生良好逻辑思维的基本训练。
提供一切活动的机会,丰富学生的数学活动的经验,从而提高动手能力,从活动中真实感受到知识。
有了线段计算的推理经验,和一些简单角度的推理运算,这个基本的角分线的求角运算完全可让学生独立完成。另外要重视将已知条件标图上的良好习惯。
六、小结 1、通过今天的学习,你学会了什么?
2、你这节课感触最深的是什么? 回顾梳理知识。
作业: 课堂练习册P92-93,B组选作。
思考:
1、把一个蛋糕等分成8份,每份中的角是多少度?如果要使每份中的角是15°,这个蛋糕应等分成多少份?
2、把一个周角7等分,每一份是多少度?(精确到分)
3、将一副三角板拼成如图的图形,
你还能求出哪些角的度数?
4、两个60?的三角板拼成一个长方
形,将其中一个翻折至虚线位置,
你能求出∠EAD的度数吗?
角度运算的递进。
拟在于提高学生的识图能力,领学生走进角的运算世界,深化知识。
锻炼翻折中图形的认识能力。
紧扣知识点,实现跳一跳够得着的知识延伸。
一、教学目标
1、会比较两个角的大小,在操作中理解角平分线的意义。
2、通过三角尺特殊角的拼画,深刻地理解角的和、差,并会进行角度的初步运算。
3、引导学生在观察、交流、实践等活动的基础上,逐渐培养动手操作能力、几何语言的表达能力以及几何识图能力,提高数学活动的经验。
4、在充分的活动体验中,让学生快乐有效地学习。
二、教学重点:角的比较,角的和、差运算。
三、教学难点:角平分线的应用及几何语言的书写。
四、教学方法:
类比思想:比线段,与比角的类比教学(从探究到书写应用)。
动手实践:角的纸板模型比较、三角板的拼画角度、角分线的作法等教学实践环节,给学生提供了充分的活动空间,体现了“做中学”的教学理念。
小组合作:教学中的几个探究活动,充分体现了小组合作的团结协作的力量,同学们的互助学习,不仅能提高学习的能力,还能增加之间的友谊,进一步促进了学习的欲望。
课件辅助:在课件演示中能生动形象地展现出“比”所体现出的方法与要领。
五、教学准备:一副三角板,几个纸板角,量角器,多媒体制作的ppt课件等。
六、教学过程:
教学环节 教 学 呈 现 教 学 意 图
一、
情景引入 引言:线段和角是几何中最基本的两个图形,线的知识我们已初步学习过了,今天进一步学习角的知识。
师:板书课题,并指出学习目标。
师:拿出如图两个角,请同学们说说,这两角谁大谁小?
学生可能有说: 红的角大,因为它的边长(或者它的整体看着大)。
也可能会说: 好像一样大,角的大小不能看边,看角度。
同学们会在各种观点中,得到启示,并开始琢磨深思。
老师适时引导:什么是角?角的两边是什么?
生:是两条射线,噢,两边是无限延伸的。
师:对,角的两边是无限延伸的,这两个角只是其中的一部分。因此角的大小比较是指度数的大小比较,与边的长短无关。 从“形”上看,度数越大,开口也越大。 通过比较边长不等的两个角的大小引入,激起学生思维火花的碰撞,老师的适时点拨,引发学生对角的定义的再次认识,得出角的比较是看角度的大小,而不是边的长短这一误区,更深刻地理解角的知识。
从“数”与“形”两方面来认识角。
二、
探知
角的比较 一、知识回顾
师:我们是怎样比较两条线段的长短?
生:各抒己见(摆在一起比,或测量长度)
师:播放两条线段比较的动画演示。
生:随着情境,用语言表达点的位置。
师:那么,怎样比较两个角的大小呢?
多媒体的动态展示,更能形象生动地体现“比”的过程。运用类比思想,为新知作铺垫。
二、活动探究
1、请同学们拿出准备好的两个角,小组讨论:
有哪些比较方法?如何比较?
教师巡视指导,观察并听取各组解决问题的方法和建议。重点辅导困难生,帮助他们获得一定的动手能力。
2、各组交流意见,最后师生共同总结方法。
课件演示:
度量法
叠合法
充分的活动时间不仅能提高学生的数学活动经验,而且给学生学会交流、学习他人的机会。
类比线段的比较方法,学生很容易想到叠合在一起去比,重点在锻炼学生的语言表达能力,以及归纳能力。
三、
探知角的运算 一、探求角的和与差:
1、给出问题:图中共有几个角?
它们之间有什么数量关系?
学生口答。
学生得出的关系可能很多,可能
会有大小关系,老师应总结出三个角
之间的和差关系。
2、练一练:口答。
∠AOD=∠AOC+__________
∠AOB=∠AOD-__________
∠BOC=∠BOD-__________
若∠AOB=∠COD,那么图中
还有两个相等的角是___________。
3、算一算。
例1 如图,∠AOB是直角,
∠BOC=34?,
求∠AOC的度数。
请一学生说说思路,
老师板书示范,要求推理格式。
学生模拟演算。
例2 如图,O是直线AB上一点,
∠AOC=53?17'。
求∠BOC的度数。
请一学生分析已知条件,说说思路。
老师板书示范,要求推理格式。
学生在理解的基础上模拟演算。感悟几何推理的逻辑性。 承上启下,有角的比较,又为角的和、差关系提供问题情境。
体现知识的关联与生长。
把形与度数的表示结合起来。
在众多角中辨清角,充实了知识。
第四问是训练学生的等量角的和的运算,是今后角度推理的重点。
例1的增加是为了示范角度求解的书写格式。
注意平角的推理,以及单位运算。
引导学生要会看已知条件,挖掘条件,并把已知标图上。
两道例题的设置,是为巩固和深化角的和、差的知识运算。从“数”与“形”两个角度进一步认识角。
二、活动探究
1、借助手中的一副三角板,你能拼出15?, 75?, 105°的角吗?你还可以拼出其他角吗?
小组探究,画出各种情况。
老师巡视指导,关注学困生使用三角板的熟练程度。
2、请学生在黑板上作画,老师帮助指导三角板的使用。
在活动中加强工具的熟练度,提高学生学习乐趣,使学生在“做中学”中深刻体会角的和与差。
小组活动,培养团结互助的良好品质。
四、
新知学习
五、
练习
应用
一、角平分线定义
师:线段的中点将线段分成相等的两部分,角有类似的现象吗?
生:仔细观察图形,并发表自己的观点。
师生共同总结:从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。
几何语言:
∵射线OB是∠AOC的角平分线,
∴∠AOB=∠BOC= ∠AOC
或∠AOC=2∠BOC = 2∠AOB
学生作笔记,感悟因果推理的表达。
类似地,还有角的三等分线:
仿照角分线让学生表达几何语言。
二、角分线作法
师:请同学们拿出你准备的一个角,如何画出它的角分线?
生:或独立完成,或同桌交流。
老师巡视观察,适当点拨设问。
请同学们展示归纳方法:折叠,折痕即为角分线。
测量,平分度数。
师:我们目前作角分线的方法,这两种即可以,只是在测量时,约平分度数即可,如何更精确地平分度数,下节课继续学。
1、如图所示,射线OE平分∠BOC,射线OD平分 ∠AOC,∠BOE=20°∠AOD=40°,求∠AOB的度数。
师:带着学生将角度标在图上。
先独立完成,要有推理过程。
再将你的书写过程与小组交流。
生:两名学生上黑板板演。
师生共同分析,注重推理及书写的格式要求。
老师启发学生思考,培养学生的分析能力。
几何语言的训练要重视,这是培养学生良好逻辑思维的基本训练。
提供一切活动的机会,丰富学生的数学活动的经验,从而提高动手能力,从活动中真实感受到知识。
有了线段计算的推理经验,和一些简单角度的推理运算,这个基本的角分线的求角运算完全可让学生独立完成。另外要重视将已知条件标图上的良好习惯。
六、小结 1、通过今天的学习,你学会了什么?
2、你这节课感触最深的是什么? 回顾梳理知识。
作业: 课堂练习册P92-93,B组选作。
思考:
1、把一个蛋糕等分成8份,每份中的角是多少度?如果要使每份中的角是15°,这个蛋糕应等分成多少份?
2、把一个周角7等分,每一份是多少度?(精确到分)
3、将一副三角板拼成如图的图形,
你还能求出哪些角的度数?
4、两个60?的三角板拼成一个长方
形,将其中一个翻折至虚线位置,
你能求出∠EAD的度数吗?
角度运算的递进。
拟在于提高学生的识图能力,领学生走进角的运算世界,深化知识。
锻炼翻折中图形的认识能力。
紧扣知识点,实现跳一跳够得着的知识延伸。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
