人教版八年级数学下册 第18章 平行四边形 单元检测试题(Word版 有答案)
文档属性
| 名称 | 人教版八年级数学下册 第18章 平行四边形 单元检测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 22:19:02 | ||
图片预览


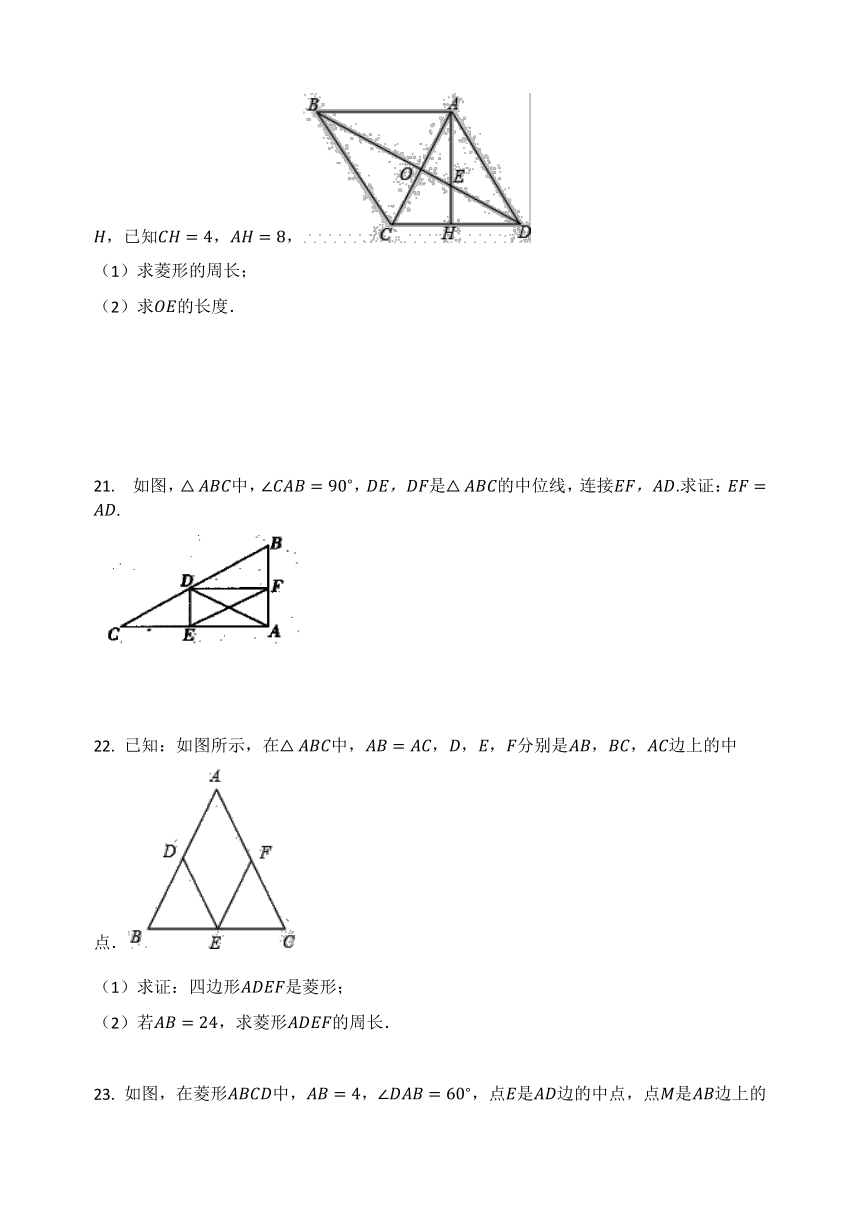
文档简介
1049020010693400123190000第18章 平行四边形 单元检测试题
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 已知直线a,b,c互相平行,直线a与b的距离是3厘米,直线b与c的距离是5厘米,那么直线a与c的距离是(? ? ? ? )
A.8厘米 B.2厘米 C.8厘米或2厘米 D.不能确定
?
2. 在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是(? ? ? ? )
A.AC=BD,AB=CD,AB?//?CD
B.AD?//?BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
?
3. 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
A.32 B.3 C.23 D.6
?
4. 已知平行四边形的两邻边长分别为18和12,若两长边的距离是6,则两短边的距离为( )
A.5 B.10 C.9 D.8
?
5. 对角线互相垂直且相等的四边形是( )
A.正方形 B.矩形 C.菱形 D.无法确定形状
?
6. 下列说法错误的是(? ? ? ? )
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直且相等的平行四边形是正方形
D.对角线相等的平行四边形是矩形
?
7. 下列说法正确的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.有三个角是直角的四边形是矩形
?
8. 《几何原本》是古希朋数学家所著的一部数学著作,共13卷,这本著作是现代数学的基础,在西方是仅次于《圣经》而流传最广的书籍.这位古希腊数学家是(????????)
A.利玛窦 B.高斯 C.李善兰 D.欧几里得
?
9. 如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )
A.四边形PNCM可能会出现为正方形
B.四边形PNCM的周长始终不变
C.当∠CPN=60?时,CP=AP
D.四边形PNCM的面积始终不变
?
10. 已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90?时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
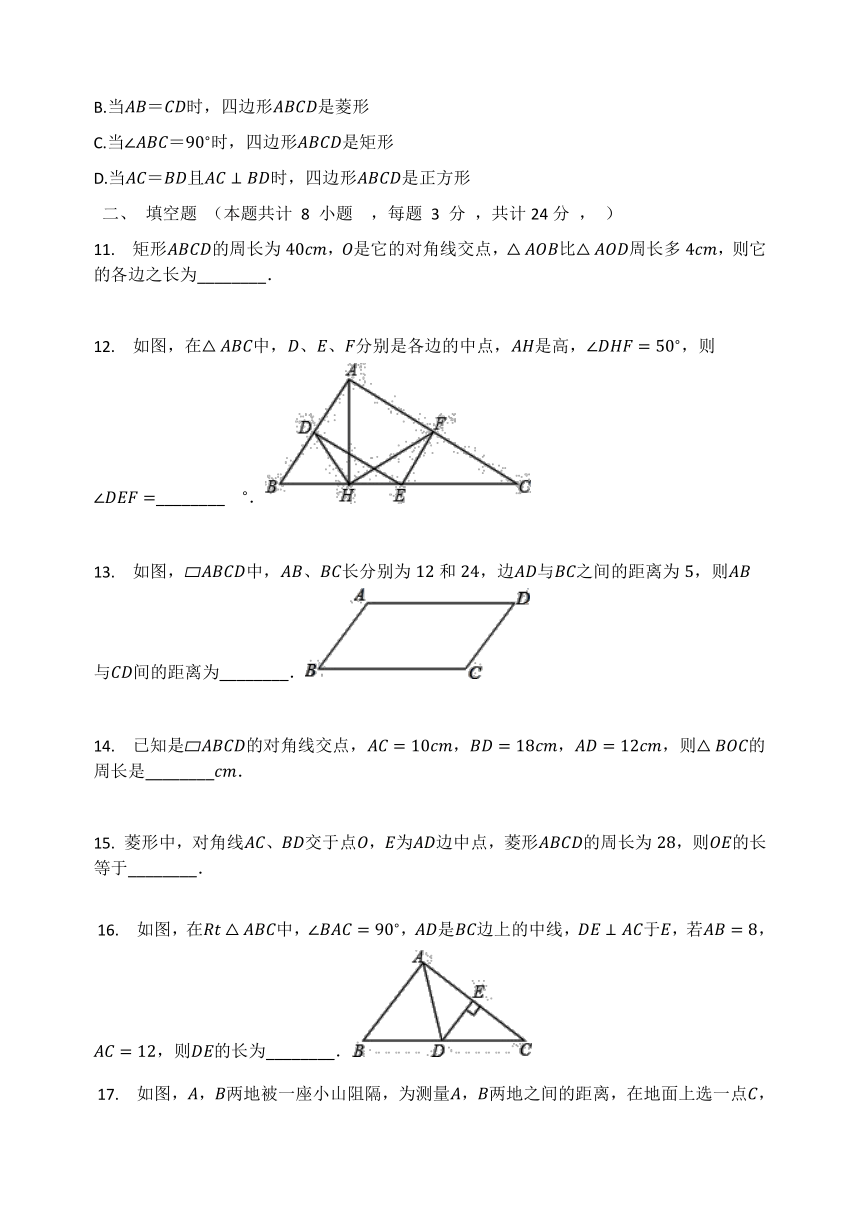
11. 矩形ABCD的周长为40cm,O是它的对角线交点,△AOB比△AOD周长多4cm,则它的各边之长为________.
?
12. 如图,在△ABC中,D、E、F分别是各边的中点,AH是高,∠DHF=50?,则∠DEF=________??.
?
13. 如图,?ABCD中,AB、BC长分别为12和24,边AD与BC之间的距离为5,则AB与CD间的距离为________.
?
14. 已知是?ABCD的对角线交点,AC=10cm,BD=18cm,AD=12cm,则△BOC的周长是________cm.
?
15. 菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于________.
?16. 如图,在Rt△ABC中,∠BAC=90?,AD是BC边上的中线,DE⊥AC于E,若AB=8,AC=12,则DE的长为________.
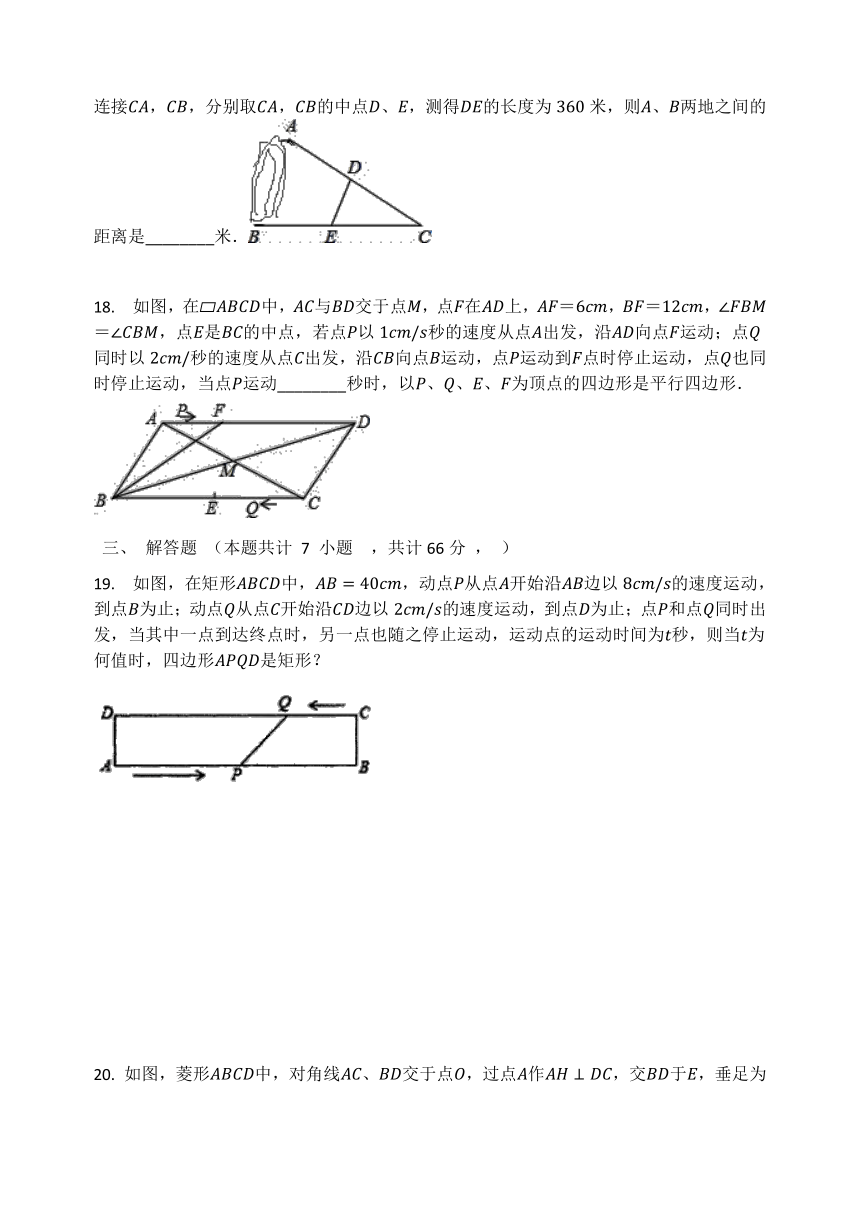
?17. 如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是________米.
?
18. 如图,在?ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动________秒时,以P、Q、E、F为顶点的四边形是平行四边形.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 如图,在矩形ABCD中,AB=40cm,动点P从点A开始沿AB边以8cm/s的速度运动,到点B为止;动点Q从点C开始沿CD边以2cm/s的速度运动,到点D为止;点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,运动点的运动时间为t秒,则当t为何值时,四边形APQD是矩形?
?
20. 如图,菱形ABCD中,对角线AC、BD交于点O,过点A作AH⊥DC,交BD于E,垂足为H,已知CH=4,AH=8,
(1)求菱形的周长;
(2)求OE的长度.
?
21. 如图,△ABC中,∠CAB=90?,DE,DF是△ABC的中位线,连接EF,AD.求证:EF=AD.
?
22. 已知:如图所示,在△ABC中,AB=AC,D,E,F分别是AB,BC,AC边上的中点.
(1)求证:四边形ADEF是菱形;
(2)若AB=24,求菱形ADEF的周长.
?
23. 如图,在菱形ABCD中,AB=4,∠DAB=60?,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)当AM的值为________时,四边形AMDN是矩形,请你把猜想出的AM值作为已知条件,说明四边形AMDN是矩形的理由.
?
24. 如图:四边形ABCD是菱形,对角线AC与BD相交于O,菱形ABCD的周长是20,BD=6.
(1)求AC的长.
(2)求菱形ABCD的高DE的长.
?
25. 已知:如图,△ABC中,D是BC上任意一点,DE?//?AC,DF?//?AB.
(1)试说明四边形AEDF的形状,并说明理由;
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:有两种情况:如图
?
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米-3厘米=2厘米;
故选C.
2.
【答案】
C
【解答】
解:A,∵ AB=CD,AB?//?CD,
∴ 四边形ABCD是平行四边形.
∵ AC=BD,
∴ 平行四边形ABCD是矩形.
故本选项错误;
B,∵ AD?//?BC,
∴ ∠A+∠B=180?,∠C+∠D=180?.
∵ ∠A=∠C,
∴ ∠B=∠D,
∴ 四边形ABCD是平行四边形.
故本选项错误;
C,
∵ AO=CO=BO=DO,∴ 四边形ABCD的对角线相等且互相平分,
∴ 四边形ABCD是矩形.
∵ AC⊥BD,
∴ 矩形ABCD是正方形.
故本选项正确;
D,
∵ AO=CO,BO=DO,∴ 四边形ABCD是平行四边形.
∵ AB=BC,
∴ 平行四边形ABCD是菱形.
故本选项错误.
故选C.
3.
【答案】
A
【解答】
解:∵ 四边形ABCD是正方形,
∴ ∠BAD=∠BCD=90?,∠PAF=∠PCE=45?,
∵ PF⊥AD,PE⊥CD,
∴ △APF和△CPE是等腰直角三角形,
∴ PF=22AP,PE=22PC,
∴ PF+PE=22(AP+PC)=22AC=32;
故选:A.
4.
【答案】
C
【解答】
解:设两短边间的距离为x,
∵ 平行四边形两邻边分别为18和12,若两长边的距离为6,
∴ 18×6=12x,
解得:x=9.
∴ 两短边间的距离为9.
故选C.
5.
【答案】
D
【解答】
解:对角线互相垂直且相等平行四边形是正方形;对角线相等的平行四边形是矩形;对角线互相垂直的平行四边形是菱形;所以无法确定其形状.
故选D.
6.
【答案】
B
【解答】
解:A,对角线互相平分的四边形是平行四边形,正确但不符合题意;
B,对角线互相垂直的平行四边形是菱形,错误,符合题意;
C,对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,所以四条边都相等的矩形是正方形,即对角线互相垂直且相等的平行四边形是正方形,正确但不符合题意;
D,对角线相等的平行四边形是矩形,正确但不符合题意.
故选B.
7.
【答案】
D
【解答】
解:A、可能是等腰梯形,故本选项错误;
B、不一定是平行四边形,故本选项错误;
C、对角线相等的平行四边形是矩形,故本选项错误;
D、有三个角是直角的四边形是矩形,故本选项正确.
故选D.
8.
【答案】
D
【解答】
解:由数学常识可知,古希腊数学家是欧几里得.
故选D.
9.
【答案】
D
【解答】
解:∵ PM=PN=CM=CN,
∴ 四边形PNCM是菱形,
当∠MCN-90?时,
四边形PNCM是正方形,
∴ A正确;
∵ 四边形PNCM的周长=4CM,CM不变,
∴ B正确;
∵ 当∠CPN=60?时,△CPN是等边三角形,
∴ CP=PN=CN,
∵ AC=CN+PN,
∴ CP=AP,
∴ C正确;
∵ 伞在撑开的过程中,四边形PNCM的面积是变化的,
∴ D不正确;
故选:D.
10.
【答案】
B
【解答】
A、根据平行四边形的性质得到OA=OC,OB=OD,该结论正确;
B、当AB=CD时,四边形ABCD还是平行四边形,该选项错误;
C、根据有一个角是直角的平行四边形是矩形可以判断该选项正确;
D、当AC=BD且AC⊥BD时,根据对角线相等可判断四边形ABCD是矩形,根据对角线互相垂直可判断四边形ABCD?是菱形,故四边形ABCD是正方形,该结论正确;
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
12cm、8cm、12cm、8cm
【解答】
解:∵ 矩形ABCD的周长为40cm,
∴ 2(AB+AD)=40,
∴ AB+AD=20①,
∵ △AOB比△AOD周长多4cm,
∴ AO+BO+AB-AO-DO-AD=4,
∵ 点O是矩形ABCD的对角线的交点,
∴ AO=BO=DO,
∴ AB-AD=4②,
联立①②解得AB=12cm,AD=8cm,
∴ BC=AD=8cm,CD=AB=12cm,
∴ 各边之长为12cm、8cm、12cm、8cm.
故答案为:12cm、8cm、12cm、8cm.
12.
【答案】
50
【解答】
解:∠DHF=∠DEF,
如图.∵ AH⊥BC于H,
又∵ D为AB的中点,
∴ DH=12AB=AD,
∴ ∠1=∠2,
同理可证:∠3=∠4,
∴ ∠1+∠3=∠2+∠4,
即∠DHF=∠DAF,
∵ E、F分别为BC、AC的中点,
∴ EF?//?AB且EF=12AB,
即EF?//?AD且EF=AD,
∴ 四边形ADEF是平行四边形,
∴ ∠DAF=∠DEF,
∴ ∠DHF=∠DEF=50?.
故答案是:50?.
13.
【答案】
10
【解答】
解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∴ 24×5=12×AF,
∴ AF=10,即AB与CD间的距离为10.
故答案是:10.
14.
【答案】
26
【解答】
解:如图,
在平行四边形ABCD中,BC=AD,
∵ AC=10cm,BD=18cm,
∴ OB=12BD=9cm,OC=12AC=5cm,
∴ △BOC的周长为OB+OC+BC=9+5+12=26cm,
故答案为:26.?
15.
【答案】
3.5
【解答】
∵ 菱形ABCD的周长为28,
∴ AB=28÷4=7,OB=OD,
∵ E为AD边中点,
∴ OE是△ABD的中位线,
∴ OE=12AB=12×7=3.5.
16.
【答案】
4
【解答】
解:∵ DE⊥AC,∠BAC=90?,
∴ DE?//?AB,
∴ CDCB=DEAB,
∵ AD是BC边上的中线,
∴ DE=12AB=4,
故答案为:4.
17.
【答案】
720
【解答】
解:∵ D、E分别是CA,CB的中点,
∴ DE是△ABC的中位线,
∴ DE?//?AB,且DE=12AB,
∵ DE=360(米),
∴ AB=360×2=720(米).
即A、B两地之间的距离是720米.
故答案为:720.
18.
【答案】
3或5
【解答】
∵ 四边形ABCD是平行四边形,
∴ AD?//?BC,AD=BC,
∴ ∠ADB=∠CBD,
∵ ∠FBM=∠CBM,
∴ ∠FBD=∠FDB,
∴ FB=FD=12cm,
∵ AF=6cm,
∴ AD=18cm,
∵ 点E是BC的中点,
∴ CE=12BC=12AD=9cm,
要使点P、Q、E、F为顶点的四边形是平行四边形,则PF=EQ即可,
设当点P运动t秒时,点P、Q、E、F为顶点的四边形是平行四边形,
根据题意得:6-t=9-2t或6-t=2t-9,
解得:t=3或t=5.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:由题意得:AP=8t,?DQ=40-2t,
∵ 四边形APQD是矩形,
∴ AP=DQ,即8t=40-2t.
解得:t=4(s).
即当t=4s时,四边形APQD是矩形.
【解答】
解:由题意得:AP=8t,?DQ=40-2t,
∵ 四边形APQD是矩形,
∴ AP=DQ,即8t=40-2t.
解得:t=4(s).
即当t=4s时,四边形APQD是矩形.
20.
【答案】
解:(1)设AD=x,则DH=x-4,在Rt△ADH中,AH2+DH2=AD2,
∴ 82+(x-4)2=x2,解得x=10,
∴ 菱形周长为40.
(2)∵ AH=8,CH=4,
∴ AC=AH2+CH2=45,
∴ CO=AO=12AC=25,
∵ BC=10,CO=25,
∴ DO=BC2-CO2=45,
∵ ∠DHE=∠DOC=90?,∠EDH=∠CDO,
∴ △DHE∽△DOC,
∴ DHDO=EHCO,
∴ 645=EH25,
∴ EH=3,
∴ AE=AH-EH=8-3=5,
∴ OE=AE2-AO2=5.
【解答】
解:(1)设AD=x,则DH=x-4,在Rt△ADH中,AH2+DH2=AD2,
∴ 82+(x-4)2=x2,解得x=10,
∴ 菱形周长为40.
(2)∵ AH=8,CH=4,
∴ AC=AH2+CH2=45,
∴ CO=AO=12AC=25,
∵ BC=10,CO=25,
∴ DO=BC2-CO2=45,
∵ ∠DHE=∠DOC=90?,∠EDH=∠CDO,
∴ △DHE∽△DOC,
∴ DHDO=EHCO,
∴ 645=EH25,
∴ EH=3,
∴ AE=AH-EH=8-3=5,
∴ OE=AE2-AO2=5.
21.
【答案】
证明:∵ DE,DF是△ABC的中位线,
∴ DE//AB,DF//AC.
∴ 四边形AEDF是平行四边形.
又∵ ∠BAC=90?,
∴ 平行四边形AEDF是矩形.
∴ EF=AD.
【解答】
证明:∵ DE,DF是△ABC的中位线,
∴ DE//AB,DF//AC.
∴ 四边形AEDF是平行四边形.
又∵ ∠BAC=90?,
∴ 平行四边形AEDF是矩形.
∴ EF=AD.
22.
【答案】
(1)证明:∵ D、E分别是AB、BC边上的中点,
∴ DE?//?AC且DE=12AC,
同理EF?//?AB,EF=12AB,
∴ 四边形ADEF是平行四边形.
又∵ AB=AC,
∴ EF=DE,
∴ 四边形ADEF是菱形.
(2)解:AB=24,则AD=12,
∴ 菱形ADEF的周长12×4=48.
【解答】
(1)证明:∵ D、E分别是AB、BC边上的中点,
∴ DE?//?AC且DE=12AC,
同理EF?//?AB,EF=12AB,
∴ 四边形ADEF是平行四边形.
又∵ AB=AC,
∴ EF=DE,
∴ 四边形ADEF是菱形.
(2)解:AB=24,则AD=12,
∴ 菱形ADEF的周长12×4=48.
23.
【答案】
解:(1)∵ 点E是AD边的中点,
∴ AE=ED,
∵ AB?//?CD,
∴ ∠NDE=∠MAE,
在△NDE和△MAE中,
∠NDE=∠MAEDE=AE∠NED=∠MEA,
∴ △NDE?△MAE(ASA),
∴ ND=AM,
∵ ND?//?AM,
∴ 四边形AMDN是平行四边形;
(2)当AM=2时,说明四边形是矩形.
∵ E是AD的中点,
∴ AE=2,
∵ AE=AM,∠EAM=60?,
∴ △AME是等边三角形,
∴ AE=EM,
∴ AE=ED=EM,
∴ ∠AMD=90?,
∵ 四边形ABCD是菱形,
故当AM=2时,四边形AMDN是矩形.
【解答】
解:(1)∵ 点E是AD边的中点,
∴ AE=ED,
∵ AB?//?CD,
∴ ∠NDE=∠MAE,
在△NDE和△MAE中,
∠NDE=∠MAEDE=AE∠NED=∠MEA,
∴ △NDE?△MAE(ASA),
∴ ND=AM,
∵ ND?//?AM,
∴ 四边形AMDN是平行四边形;
(2)当AM=2时,说明四边形是矩形.
∵ E是AD的中点,
∴ AE=2,
∵ AE=AM,∠EAM=60?,
∴ △AME是等边三角形,
∴ AE=EM,
∴ AE=ED=EM,
∴ ∠AMD=90?,
∵ 四边形ABCD是菱形,
故当AM=2时,四边形AMDN是矩形.
24.
【答案】
解:(1)∵ 四边形ABCD是菱形,
∴ AB=BC=CD=AD,
AC⊥BD,BO=OD,AO=OC.
∵ 菱形的周长是20,
∴ DC=14×20=5.???????????????????????
∵ BD=6,∴ OD=3.
在Rt△DOC中
OC=DC2-OD2
=52-32
=4.
∴ AC=2OC=8.???????????????????????????
(2)∵ S△ABD=12AB?DE=12BD?OA,
∴ 5?DE=6×4
∴ DE=245.??????????????????????????????
【解答】
解:(1)∵ 四边形ABCD是菱形,
∴ AB=BC=CD=AD,
AC⊥BD,BO=OD,AO=OC.
∵ 菱形的周长是20,
∴ DC=14×20=5.???????????????????????
∵ BD=6,∴ OD=3.
在Rt△DOC中
OC=DC2-OD2
=52-32
=4.
∴ AC=2OC=8.???????????????????????????
(2)∵ S△ABD=12AB?DE=12BD?OA,
∴ 5?DE=6×4
∴ DE=245.??????????????????????????????
25.
【答案】
解:(1)∵ DE?//?AC,DF?//?AB,
∴ DE//AF,DF//AE
∴ 四边形AEDF为平行四边形;
(2)∵ 四边形AEDF为菱形,
∴ AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
(3)由四边形AEDF为正方形,∴ ∠BAC=90?,
∴ △ABC是以BC为斜边的直角三角形即可.
【解答】
解:(1)∵ DE?//?AC,DF?//?AB,
∴ DE//AF,DF//AE
∴ 四边形AEDF为平行四边形;
(2)∵ 四边形AEDF为菱形,
∴ AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
(3)由四边形AEDF为正方形,∴ ∠BAC=90?,
∴ △ABC是以BC为斜边的直角三角形即可.
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 已知直线a,b,c互相平行,直线a与b的距离是3厘米,直线b与c的距离是5厘米,那么直线a与c的距离是(? ? ? ? )
A.8厘米 B.2厘米 C.8厘米或2厘米 D.不能确定
?
2. 在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是(? ? ? ? )
A.AC=BD,AB=CD,AB?//?CD
B.AD?//?BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
?
3. 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
A.32 B.3 C.23 D.6
?
4. 已知平行四边形的两邻边长分别为18和12,若两长边的距离是6,则两短边的距离为( )
A.5 B.10 C.9 D.8
?
5. 对角线互相垂直且相等的四边形是( )
A.正方形 B.矩形 C.菱形 D.无法确定形状
?
6. 下列说法错误的是(? ? ? ? )
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直且相等的平行四边形是正方形
D.对角线相等的平行四边形是矩形
?
7. 下列说法正确的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.有三个角是直角的四边形是矩形
?
8. 《几何原本》是古希朋数学家所著的一部数学著作,共13卷,这本著作是现代数学的基础,在西方是仅次于《圣经》而流传最广的书籍.这位古希腊数学家是(????????)
A.利玛窦 B.高斯 C.李善兰 D.欧几里得
?
9. 如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )
A.四边形PNCM可能会出现为正方形
B.四边形PNCM的周长始终不变
C.当∠CPN=60?时,CP=AP
D.四边形PNCM的面积始终不变
?
10. 已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90?时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
11. 矩形ABCD的周长为40cm,O是它的对角线交点,△AOB比△AOD周长多4cm,则它的各边之长为________.
?
12. 如图,在△ABC中,D、E、F分别是各边的中点,AH是高,∠DHF=50?,则∠DEF=________??.
?
13. 如图,?ABCD中,AB、BC长分别为12和24,边AD与BC之间的距离为5,则AB与CD间的距离为________.
?
14. 已知是?ABCD的对角线交点,AC=10cm,BD=18cm,AD=12cm,则△BOC的周长是________cm.
?
15. 菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于________.
?16. 如图,在Rt△ABC中,∠BAC=90?,AD是BC边上的中线,DE⊥AC于E,若AB=8,AC=12,则DE的长为________.
?17. 如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是________米.
?
18. 如图,在?ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动________秒时,以P、Q、E、F为顶点的四边形是平行四边形.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 如图,在矩形ABCD中,AB=40cm,动点P从点A开始沿AB边以8cm/s的速度运动,到点B为止;动点Q从点C开始沿CD边以2cm/s的速度运动,到点D为止;点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,运动点的运动时间为t秒,则当t为何值时,四边形APQD是矩形?
?
20. 如图,菱形ABCD中,对角线AC、BD交于点O,过点A作AH⊥DC,交BD于E,垂足为H,已知CH=4,AH=8,
(1)求菱形的周长;
(2)求OE的长度.
?
21. 如图,△ABC中,∠CAB=90?,DE,DF是△ABC的中位线,连接EF,AD.求证:EF=AD.
?
22. 已知:如图所示,在△ABC中,AB=AC,D,E,F分别是AB,BC,AC边上的中点.
(1)求证:四边形ADEF是菱形;
(2)若AB=24,求菱形ADEF的周长.
?
23. 如图,在菱形ABCD中,AB=4,∠DAB=60?,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)当AM的值为________时,四边形AMDN是矩形,请你把猜想出的AM值作为已知条件,说明四边形AMDN是矩形的理由.
?
24. 如图:四边形ABCD是菱形,对角线AC与BD相交于O,菱形ABCD的周长是20,BD=6.
(1)求AC的长.
(2)求菱形ABCD的高DE的长.
?
25. 已知:如图,△ABC中,D是BC上任意一点,DE?//?AC,DF?//?AB.
(1)试说明四边形AEDF的形状,并说明理由;
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:有两种情况:如图
?
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米-3厘米=2厘米;
故选C.
2.
【答案】
C
【解答】
解:A,∵ AB=CD,AB?//?CD,
∴ 四边形ABCD是平行四边形.
∵ AC=BD,
∴ 平行四边形ABCD是矩形.
故本选项错误;
B,∵ AD?//?BC,
∴ ∠A+∠B=180?,∠C+∠D=180?.
∵ ∠A=∠C,
∴ ∠B=∠D,
∴ 四边形ABCD是平行四边形.
故本选项错误;
C,
∵ AO=CO=BO=DO,∴ 四边形ABCD的对角线相等且互相平分,
∴ 四边形ABCD是矩形.
∵ AC⊥BD,
∴ 矩形ABCD是正方形.
故本选项正确;
D,
∵ AO=CO,BO=DO,∴ 四边形ABCD是平行四边形.
∵ AB=BC,
∴ 平行四边形ABCD是菱形.
故本选项错误.
故选C.
3.
【答案】
A
【解答】
解:∵ 四边形ABCD是正方形,
∴ ∠BAD=∠BCD=90?,∠PAF=∠PCE=45?,
∵ PF⊥AD,PE⊥CD,
∴ △APF和△CPE是等腰直角三角形,
∴ PF=22AP,PE=22PC,
∴ PF+PE=22(AP+PC)=22AC=32;
故选:A.
4.
【答案】
C
【解答】
解:设两短边间的距离为x,
∵ 平行四边形两邻边分别为18和12,若两长边的距离为6,
∴ 18×6=12x,
解得:x=9.
∴ 两短边间的距离为9.
故选C.
5.
【答案】
D
【解答】
解:对角线互相垂直且相等平行四边形是正方形;对角线相等的平行四边形是矩形;对角线互相垂直的平行四边形是菱形;所以无法确定其形状.
故选D.
6.
【答案】
B
【解答】
解:A,对角线互相平分的四边形是平行四边形,正确但不符合题意;
B,对角线互相垂直的平行四边形是菱形,错误,符合题意;
C,对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,所以四条边都相等的矩形是正方形,即对角线互相垂直且相等的平行四边形是正方形,正确但不符合题意;
D,对角线相等的平行四边形是矩形,正确但不符合题意.
故选B.
7.
【答案】
D
【解答】
解:A、可能是等腰梯形,故本选项错误;
B、不一定是平行四边形,故本选项错误;
C、对角线相等的平行四边形是矩形,故本选项错误;
D、有三个角是直角的四边形是矩形,故本选项正确.
故选D.
8.
【答案】
D
【解答】
解:由数学常识可知,古希腊数学家是欧几里得.
故选D.
9.
【答案】
D
【解答】
解:∵ PM=PN=CM=CN,
∴ 四边形PNCM是菱形,
当∠MCN-90?时,
四边形PNCM是正方形,
∴ A正确;
∵ 四边形PNCM的周长=4CM,CM不变,
∴ B正确;
∵ 当∠CPN=60?时,△CPN是等边三角形,
∴ CP=PN=CN,
∵ AC=CN+PN,
∴ CP=AP,
∴ C正确;
∵ 伞在撑开的过程中,四边形PNCM的面积是变化的,
∴ D不正确;
故选:D.
10.
【答案】
B
【解答】
A、根据平行四边形的性质得到OA=OC,OB=OD,该结论正确;
B、当AB=CD时,四边形ABCD还是平行四边形,该选项错误;
C、根据有一个角是直角的平行四边形是矩形可以判断该选项正确;
D、当AC=BD且AC⊥BD时,根据对角线相等可判断四边形ABCD是矩形,根据对角线互相垂直可判断四边形ABCD?是菱形,故四边形ABCD是正方形,该结论正确;
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
12cm、8cm、12cm、8cm
【解答】
解:∵ 矩形ABCD的周长为40cm,
∴ 2(AB+AD)=40,
∴ AB+AD=20①,
∵ △AOB比△AOD周长多4cm,
∴ AO+BO+AB-AO-DO-AD=4,
∵ 点O是矩形ABCD的对角线的交点,
∴ AO=BO=DO,
∴ AB-AD=4②,
联立①②解得AB=12cm,AD=8cm,
∴ BC=AD=8cm,CD=AB=12cm,
∴ 各边之长为12cm、8cm、12cm、8cm.
故答案为:12cm、8cm、12cm、8cm.
12.
【答案】
50
【解答】
解:∠DHF=∠DEF,
如图.∵ AH⊥BC于H,
又∵ D为AB的中点,
∴ DH=12AB=AD,
∴ ∠1=∠2,
同理可证:∠3=∠4,
∴ ∠1+∠3=∠2+∠4,
即∠DHF=∠DAF,
∵ E、F分别为BC、AC的中点,
∴ EF?//?AB且EF=12AB,
即EF?//?AD且EF=AD,
∴ 四边形ADEF是平行四边形,
∴ ∠DAF=∠DEF,
∴ ∠DHF=∠DEF=50?.
故答案是:50?.
13.
【答案】
10
【解答】
解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∴ 24×5=12×AF,
∴ AF=10,即AB与CD间的距离为10.
故答案是:10.
14.
【答案】
26
【解答】
解:如图,
在平行四边形ABCD中,BC=AD,
∵ AC=10cm,BD=18cm,
∴ OB=12BD=9cm,OC=12AC=5cm,
∴ △BOC的周长为OB+OC+BC=9+5+12=26cm,
故答案为:26.?
15.
【答案】
3.5
【解答】
∵ 菱形ABCD的周长为28,
∴ AB=28÷4=7,OB=OD,
∵ E为AD边中点,
∴ OE是△ABD的中位线,
∴ OE=12AB=12×7=3.5.
16.
【答案】
4
【解答】
解:∵ DE⊥AC,∠BAC=90?,
∴ DE?//?AB,
∴ CDCB=DEAB,
∵ AD是BC边上的中线,
∴ DE=12AB=4,
故答案为:4.
17.
【答案】
720
【解答】
解:∵ D、E分别是CA,CB的中点,
∴ DE是△ABC的中位线,
∴ DE?//?AB,且DE=12AB,
∵ DE=360(米),
∴ AB=360×2=720(米).
即A、B两地之间的距离是720米.
故答案为:720.
18.
【答案】
3或5
【解答】
∵ 四边形ABCD是平行四边形,
∴ AD?//?BC,AD=BC,
∴ ∠ADB=∠CBD,
∵ ∠FBM=∠CBM,
∴ ∠FBD=∠FDB,
∴ FB=FD=12cm,
∵ AF=6cm,
∴ AD=18cm,
∵ 点E是BC的中点,
∴ CE=12BC=12AD=9cm,
要使点P、Q、E、F为顶点的四边形是平行四边形,则PF=EQ即可,
设当点P运动t秒时,点P、Q、E、F为顶点的四边形是平行四边形,
根据题意得:6-t=9-2t或6-t=2t-9,
解得:t=3或t=5.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:由题意得:AP=8t,?DQ=40-2t,
∵ 四边形APQD是矩形,
∴ AP=DQ,即8t=40-2t.
解得:t=4(s).
即当t=4s时,四边形APQD是矩形.
【解答】
解:由题意得:AP=8t,?DQ=40-2t,
∵ 四边形APQD是矩形,
∴ AP=DQ,即8t=40-2t.
解得:t=4(s).
即当t=4s时,四边形APQD是矩形.
20.
【答案】
解:(1)设AD=x,则DH=x-4,在Rt△ADH中,AH2+DH2=AD2,
∴ 82+(x-4)2=x2,解得x=10,
∴ 菱形周长为40.
(2)∵ AH=8,CH=4,
∴ AC=AH2+CH2=45,
∴ CO=AO=12AC=25,
∵ BC=10,CO=25,
∴ DO=BC2-CO2=45,
∵ ∠DHE=∠DOC=90?,∠EDH=∠CDO,
∴ △DHE∽△DOC,
∴ DHDO=EHCO,
∴ 645=EH25,
∴ EH=3,
∴ AE=AH-EH=8-3=5,
∴ OE=AE2-AO2=5.
【解答】
解:(1)设AD=x,则DH=x-4,在Rt△ADH中,AH2+DH2=AD2,
∴ 82+(x-4)2=x2,解得x=10,
∴ 菱形周长为40.
(2)∵ AH=8,CH=4,
∴ AC=AH2+CH2=45,
∴ CO=AO=12AC=25,
∵ BC=10,CO=25,
∴ DO=BC2-CO2=45,
∵ ∠DHE=∠DOC=90?,∠EDH=∠CDO,
∴ △DHE∽△DOC,
∴ DHDO=EHCO,
∴ 645=EH25,
∴ EH=3,
∴ AE=AH-EH=8-3=5,
∴ OE=AE2-AO2=5.
21.
【答案】
证明:∵ DE,DF是△ABC的中位线,
∴ DE//AB,DF//AC.
∴ 四边形AEDF是平行四边形.
又∵ ∠BAC=90?,
∴ 平行四边形AEDF是矩形.
∴ EF=AD.
【解答】
证明:∵ DE,DF是△ABC的中位线,
∴ DE//AB,DF//AC.
∴ 四边形AEDF是平行四边形.
又∵ ∠BAC=90?,
∴ 平行四边形AEDF是矩形.
∴ EF=AD.
22.
【答案】
(1)证明:∵ D、E分别是AB、BC边上的中点,
∴ DE?//?AC且DE=12AC,
同理EF?//?AB,EF=12AB,
∴ 四边形ADEF是平行四边形.
又∵ AB=AC,
∴ EF=DE,
∴ 四边形ADEF是菱形.
(2)解:AB=24,则AD=12,
∴ 菱形ADEF的周长12×4=48.
【解答】
(1)证明:∵ D、E分别是AB、BC边上的中点,
∴ DE?//?AC且DE=12AC,
同理EF?//?AB,EF=12AB,
∴ 四边形ADEF是平行四边形.
又∵ AB=AC,
∴ EF=DE,
∴ 四边形ADEF是菱形.
(2)解:AB=24,则AD=12,
∴ 菱形ADEF的周长12×4=48.
23.
【答案】
解:(1)∵ 点E是AD边的中点,
∴ AE=ED,
∵ AB?//?CD,
∴ ∠NDE=∠MAE,
在△NDE和△MAE中,
∠NDE=∠MAEDE=AE∠NED=∠MEA,
∴ △NDE?△MAE(ASA),
∴ ND=AM,
∵ ND?//?AM,
∴ 四边形AMDN是平行四边形;
(2)当AM=2时,说明四边形是矩形.
∵ E是AD的中点,
∴ AE=2,
∵ AE=AM,∠EAM=60?,
∴ △AME是等边三角形,
∴ AE=EM,
∴ AE=ED=EM,
∴ ∠AMD=90?,
∵ 四边形ABCD是菱形,
故当AM=2时,四边形AMDN是矩形.
【解答】
解:(1)∵ 点E是AD边的中点,
∴ AE=ED,
∵ AB?//?CD,
∴ ∠NDE=∠MAE,
在△NDE和△MAE中,
∠NDE=∠MAEDE=AE∠NED=∠MEA,
∴ △NDE?△MAE(ASA),
∴ ND=AM,
∵ ND?//?AM,
∴ 四边形AMDN是平行四边形;
(2)当AM=2时,说明四边形是矩形.
∵ E是AD的中点,
∴ AE=2,
∵ AE=AM,∠EAM=60?,
∴ △AME是等边三角形,
∴ AE=EM,
∴ AE=ED=EM,
∴ ∠AMD=90?,
∵ 四边形ABCD是菱形,
故当AM=2时,四边形AMDN是矩形.
24.
【答案】
解:(1)∵ 四边形ABCD是菱形,
∴ AB=BC=CD=AD,
AC⊥BD,BO=OD,AO=OC.
∵ 菱形的周长是20,
∴ DC=14×20=5.???????????????????????
∵ BD=6,∴ OD=3.
在Rt△DOC中
OC=DC2-OD2
=52-32
=4.
∴ AC=2OC=8.???????????????????????????
(2)∵ S△ABD=12AB?DE=12BD?OA,
∴ 5?DE=6×4
∴ DE=245.??????????????????????????????
【解答】
解:(1)∵ 四边形ABCD是菱形,
∴ AB=BC=CD=AD,
AC⊥BD,BO=OD,AO=OC.
∵ 菱形的周长是20,
∴ DC=14×20=5.???????????????????????
∵ BD=6,∴ OD=3.
在Rt△DOC中
OC=DC2-OD2
=52-32
=4.
∴ AC=2OC=8.???????????????????????????
(2)∵ S△ABD=12AB?DE=12BD?OA,
∴ 5?DE=6×4
∴ DE=245.??????????????????????????????
25.
【答案】
解:(1)∵ DE?//?AC,DF?//?AB,
∴ DE//AF,DF//AE
∴ 四边形AEDF为平行四边形;
(2)∵ 四边形AEDF为菱形,
∴ AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
(3)由四边形AEDF为正方形,∴ ∠BAC=90?,
∴ △ABC是以BC为斜边的直角三角形即可.
【解答】
解:(1)∵ DE?//?AC,DF?//?AB,
∴ DE//AF,DF//AE
∴ 四边形AEDF为平行四边形;
(2)∵ 四边形AEDF为菱形,
∴ AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
(3)由四边形AEDF为正方形,∴ ∠BAC=90?,
∴ △ABC是以BC为斜边的直角三角形即可.
