人教版数学七年级下册 8.3实际问题与二元一次方程组同步测试试题(一) (word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 8.3实际问题与二元一次方程组同步测试试题(一) (word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 160.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:12:32 | ||
图片预览



文档简介
实际问题与二元一次方程组同步测试试题(一)
一.选择题
1.某次足球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,某球队参赛15场,积33分,若不考虑比赛顺序,则该队胜、平、负的情况可能有( )
A.15种
B.11种
C.5种
D.3种
2.今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱,问人数、物价各多少?设有x人,商品的价格为y,依题意可列方程组为( )
A.
B.
C.
D.
3.《九章算术》中有一道题的条件是:“今有大器五一容三斛,大器一小器五容二斛.”大致意思是:有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,依据该条件,1大桶加1小桶共盛( )斛米.(注:斛是古代一种容量单位)
A.
B.
C.1
D.
4.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则y﹣x=( )
A.2
B.4
C.﹣6
D.6
5.《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有x个人,该物品价格是y元,则下列方程组正确的是( )
A.
B.
C.
D.
6.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为xcm和ycm,则两个小长方形的面积是( )
A.1200
B.1600
C.1800
D.2400
7.陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定弄错了.”陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,那么笔记本的单价可能是( )元.
A.1元
B.2元
C.3元
D.4元
8.小明、小颖、小亮玩飞镖游戏,他们每人投靶5次,中靶情况如图所示.规定投中同一圆环得分相同,若小明得分21分,小亮得分17分,则小颖得分为( )
A.19分
B.20分
C.21分
D.22分
9.已知梯形的高是7cm,面积是56cm2,它的上底比下底的三分之一还多4cm,求该梯形的上底和下底的长度是多少?设上底为xcm,下底为ycm,则可以列方程组为( )
A.
B.
C.
D.
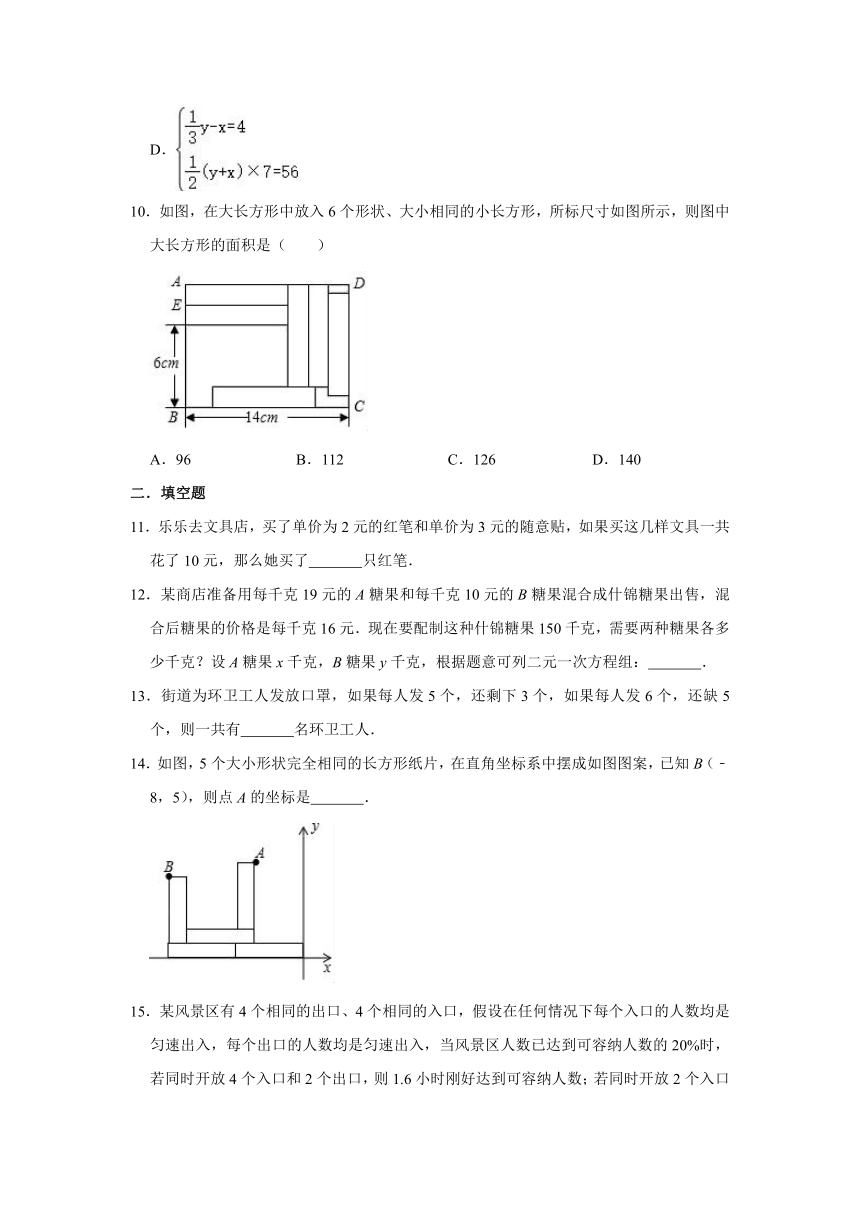
10.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是( )
A.96
B.112
C.126
D.140
二.填空题
11.乐乐去文具店,买了单价为2元的红笔和单价为3元的随意贴,如果买这几样文具一共花了10元,那么她买了
只红笔.
12.某商店准备用每千克19元的A糖果和每千克10元的B糖果混合成什锦糖果出售,混合后糖果的价格是每千克16元.现在要配制这种什锦糖果150千克,需要两种糖果各多少千克?设A糖果x千克,B糖果y千克,根据题意可列二元一次方程组:
.
13.街道为环卫工人发放口罩,如果每人发5个,还剩下3个,如果每人发6个,还缺5个,则一共有
名环卫工人.
14.如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知B(﹣8,5),则点A的坐标是
.
15.某风景区有4个相同的出口、4个相同的入口,假设在任何情况下每个入口的人数均是匀速出入,每个出口的人数均是匀速出入,当风景区人数已达到可容纳人数的20%时,若同时开放4个入口和2个出口,则1.6小时刚好达到可容纳人数;若同时开放2个入口和2个出口,则8小时刚好达到可容纳人数.受疫情影响,2020年五一期间,该风景区游览人数只允许达到平时可容纳人数的60%,当风景区人数已达到平时可容纳人数的10%时,若同时开放3个入口和2个出口,则经过
小时刚好达到平时可容纳人数的60%.
三.解答题
16.某旅馆的客房有三人间和两人间两种.三人间每人每天80元,两人间每人每天100元,一个50人的旅游团到该旅馆住宿,租住了若干客房,且每个房间正好住满,一天共花去住宿费4520元,两种客房各租住了多少间?
17.为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户.若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.
(1)求医用口罩和洗手液的单价;
(2)由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N95口罩.若需购买医用口罩,N95口罩共1200个,其中N95口罩不超过200个,钱恰好全部用完,则有几种购买方案,请列方程计算.
18.某电器公司计划装运甲、乙两种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电),已知每辆汽车可装运甲种家电20台,乙种家电15台.
(1)若用8辆汽车装运甲、乙两种家电共150台到A地销售,问装运甲、乙两种家电的汽车各有多少辆?(列二元一次方程组解应用题)
(2)如果每台甲种家电的利润是100元,每台乙种家电的利润是200元,那么该公司售完这150台家电后的总利润是多少?
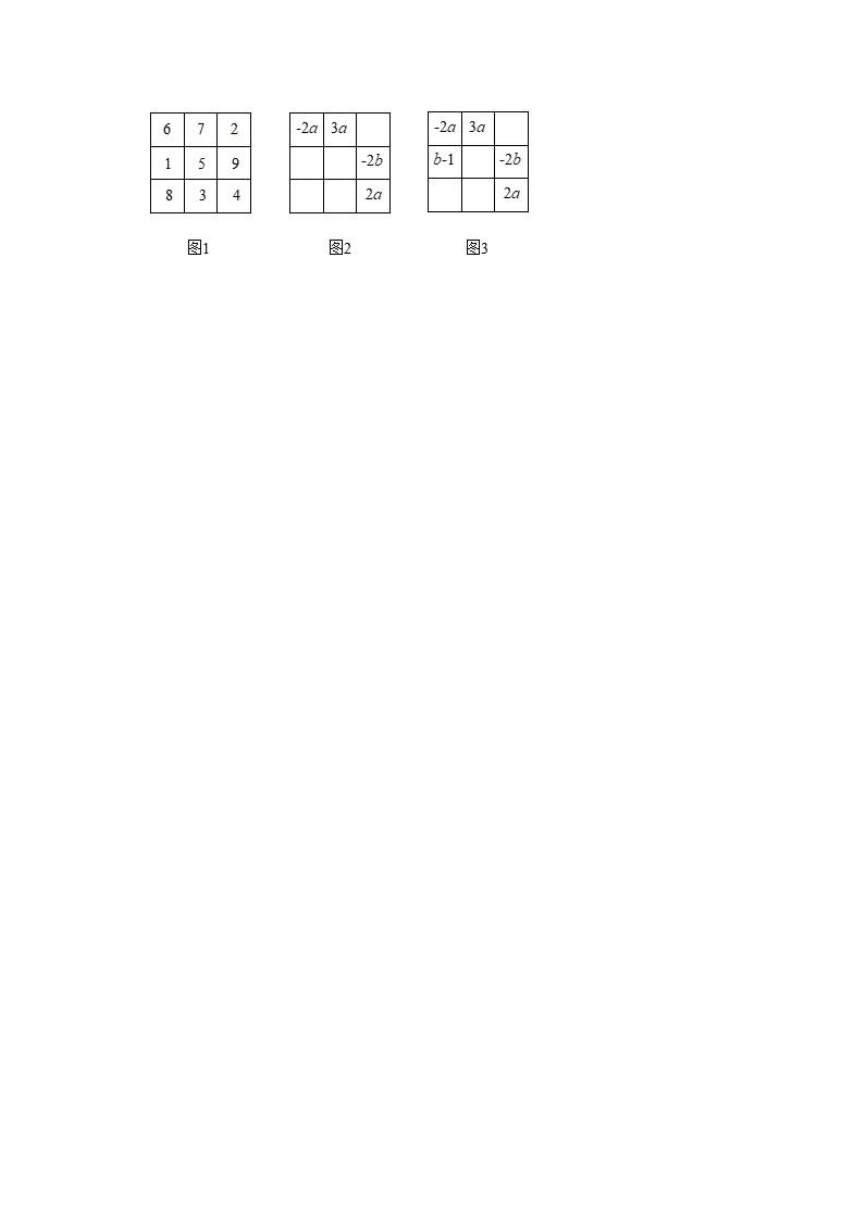
19.在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”.如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
(1)图2是显示部分代数式的“等和格”,可得a=
.图3是显示部分代数式的“等和格”,可得a=
.b=
.
参考答案与试题解析
一.选择题
1.【解答】解:设胜的场数为x,平的场数为y,那么负的场数为(15﹣x﹣y)
3x+y+0(15﹣x﹣y)=33
y=33﹣3x
x,y为正整数或0,x+y≤15
故选:D.
2.【解答】解:设有x人,商品的价格为y,
依题意,得.
故选:D.
3.【解答】解:设1大桶可盛x斛米,1小桶可盛y斛米,
依题意,得:,
解得:,
∴x+y=+=.
故选:B.
4.【解答】解:依题意,得,
解得,
∴y﹣x=﹣6.
故选:C.
5.【解答】解:若设有x人,物品价值y元,根据题意,可列方程组为,
故选:C.
6.【解答】解:依题意,得:,
解得:,
∴2xy=2×60×20=2400.
故选:D.
7.【解答】解:设购买单价为8元的书x本,笔记本的单价为y元,则购买单价为12元的书(105﹣x)本,
依题意,得:8x+y+12(105﹣x)=1500﹣418,
∴y=178﹣4x,
又∵x,y均为正整数,且y<5,
∴x=44,y=2.
故选:B.
8.【解答】解:设投中内环得x分,投中外环得y分,
依题意,得:,
解得:,
∴2x+3y=2×5+3×3=19.
故选:A.
9.【解答】解:设上底为xcm,下底为ycm,
根据题意可以列方程组为,
故选:C.
10.【解答】解:设小长方形的长、宽分别为xcm,ycm,
依题意得,
解之得,
∴小长方形的长、宽分别为8cm,2cm,
∴S大长方形=ABBC=14×10=140cm2,
故选:D.
二.填空题(共5小题)
11.【解答】解:设买了x只红笔,y本随意贴,根据题意可得:2x+3y=10,
∵笔和随意贴的数目是整数,
∴x=2,y=2,
答:她买了2支红笔,
故答案为:2.
12.【解答】解:设需要每千克19元的糖果x千克,每千克10元糖果y千克,根据题意可得:,
故答案为:.
13.【解答】解:设一共有x名环卫工人,要发放的口罩共有y个,
依题意,得:,
解得:.
故答案为:8.
14.【解答】解:设长方形纸片的长为x,宽为y,
依题意,得:,
解得:,
∴x﹣y=3,x+2y=6,
∴点A的坐标为(﹣3,6).
故答案为:(﹣3,6).
15.【解答】解:设每个入口每小时可进可容纳人数的x%,每个出口每小时可出可容纳人数的y%,
依题意,得:,
解得:,
∴==.
故答案为:.
三.解答题(共4小题)
16.【解答】解:设三人间租住了x间,两人间租住了y间,
依题意,得:,
解得:.
答:三人间租住了8间,两人间租住了13间.
17.【解答】解:(1)设医用口罩的单价为x元/个,洗手液的单价为y元/瓶,
根据题意得:,
解得:,
答:医用口罩的单价为2.5
元/个,洗手液的单价为30元/瓶;
(2)设增加购买N95口罩a个,洗手液b瓶,则医用口罩(1200﹣a)个,
根据题意得:6a+2.5(1200﹣a)+30b=5400,
化简,得:7a+60b=4800,
∴b=80﹣,
∵a,b都为正整数,
∴a为60的倍数,且a≤200,
∴,,,
∴有三种购买方案.
18.【解答】解:(1)设装运甲种家电的汽车有x辆,装运乙种家电的汽车有y辆,
依题意,得:,
解得:.
答:装运甲种家电的汽车有6辆,装运乙种家电的汽车有2辆.
(2)100×20×6+200×15×2=18000(元).
答:该公司售完这150台家电后的总利润是18000元.
19.【解答】解:(1)由题意得:﹣2a+3a=﹣2b+2a,
则﹣a=﹣2b,
故a=2b.
故答案为:a=2b;
(2)由题意得:﹣2a+2a=b﹣1+(﹣2b),
解得b=﹣1,
由(1)得a=2b,
则a=﹣2.
故答案为:﹣2,﹣1.
一.选择题
1.某次足球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,某球队参赛15场,积33分,若不考虑比赛顺序,则该队胜、平、负的情况可能有( )
A.15种
B.11种
C.5种
D.3种
2.今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱,问人数、物价各多少?设有x人,商品的价格为y,依题意可列方程组为( )
A.
B.
C.
D.
3.《九章算术》中有一道题的条件是:“今有大器五一容三斛,大器一小器五容二斛.”大致意思是:有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,依据该条件,1大桶加1小桶共盛( )斛米.(注:斛是古代一种容量单位)
A.
B.
C.1
D.
4.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则y﹣x=( )
A.2
B.4
C.﹣6
D.6
5.《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有x个人,该物品价格是y元,则下列方程组正确的是( )
A.
B.
C.
D.
6.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为xcm和ycm,则两个小长方形的面积是( )
A.1200
B.1600
C.1800
D.2400
7.陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定弄错了.”陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,那么笔记本的单价可能是( )元.
A.1元
B.2元
C.3元
D.4元
8.小明、小颖、小亮玩飞镖游戏,他们每人投靶5次,中靶情况如图所示.规定投中同一圆环得分相同,若小明得分21分,小亮得分17分,则小颖得分为( )
A.19分
B.20分
C.21分
D.22分
9.已知梯形的高是7cm,面积是56cm2,它的上底比下底的三分之一还多4cm,求该梯形的上底和下底的长度是多少?设上底为xcm,下底为ycm,则可以列方程组为( )
A.
B.
C.
D.
10.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是( )
A.96
B.112
C.126
D.140
二.填空题
11.乐乐去文具店,买了单价为2元的红笔和单价为3元的随意贴,如果买这几样文具一共花了10元,那么她买了
只红笔.
12.某商店准备用每千克19元的A糖果和每千克10元的B糖果混合成什锦糖果出售,混合后糖果的价格是每千克16元.现在要配制这种什锦糖果150千克,需要两种糖果各多少千克?设A糖果x千克,B糖果y千克,根据题意可列二元一次方程组:
.
13.街道为环卫工人发放口罩,如果每人发5个,还剩下3个,如果每人发6个,还缺5个,则一共有
名环卫工人.
14.如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知B(﹣8,5),则点A的坐标是
.
15.某风景区有4个相同的出口、4个相同的入口,假设在任何情况下每个入口的人数均是匀速出入,每个出口的人数均是匀速出入,当风景区人数已达到可容纳人数的20%时,若同时开放4个入口和2个出口,则1.6小时刚好达到可容纳人数;若同时开放2个入口和2个出口,则8小时刚好达到可容纳人数.受疫情影响,2020年五一期间,该风景区游览人数只允许达到平时可容纳人数的60%,当风景区人数已达到平时可容纳人数的10%时,若同时开放3个入口和2个出口,则经过
小时刚好达到平时可容纳人数的60%.
三.解答题
16.某旅馆的客房有三人间和两人间两种.三人间每人每天80元,两人间每人每天100元,一个50人的旅游团到该旅馆住宿,租住了若干客房,且每个房间正好住满,一天共花去住宿费4520元,两种客房各租住了多少间?
17.为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户.若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.
(1)求医用口罩和洗手液的单价;
(2)由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N95口罩.若需购买医用口罩,N95口罩共1200个,其中N95口罩不超过200个,钱恰好全部用完,则有几种购买方案,请列方程计算.
18.某电器公司计划装运甲、乙两种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电),已知每辆汽车可装运甲种家电20台,乙种家电15台.
(1)若用8辆汽车装运甲、乙两种家电共150台到A地销售,问装运甲、乙两种家电的汽车各有多少辆?(列二元一次方程组解应用题)
(2)如果每台甲种家电的利润是100元,每台乙种家电的利润是200元,那么该公司售完这150台家电后的总利润是多少?
19.在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”.如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
(1)图2是显示部分代数式的“等和格”,可得a=
.图3是显示部分代数式的“等和格”,可得a=
.b=
.
参考答案与试题解析
一.选择题
1.【解答】解:设胜的场数为x,平的场数为y,那么负的场数为(15﹣x﹣y)
3x+y+0(15﹣x﹣y)=33
y=33﹣3x
x,y为正整数或0,x+y≤15
故选:D.
2.【解答】解:设有x人,商品的价格为y,
依题意,得.
故选:D.
3.【解答】解:设1大桶可盛x斛米,1小桶可盛y斛米,
依题意,得:,
解得:,
∴x+y=+=.
故选:B.
4.【解答】解:依题意,得,
解得,
∴y﹣x=﹣6.
故选:C.
5.【解答】解:若设有x人,物品价值y元,根据题意,可列方程组为,
故选:C.
6.【解答】解:依题意,得:,
解得:,
∴2xy=2×60×20=2400.
故选:D.
7.【解答】解:设购买单价为8元的书x本,笔记本的单价为y元,则购买单价为12元的书(105﹣x)本,
依题意,得:8x+y+12(105﹣x)=1500﹣418,
∴y=178﹣4x,
又∵x,y均为正整数,且y<5,
∴x=44,y=2.
故选:B.
8.【解答】解:设投中内环得x分,投中外环得y分,
依题意,得:,
解得:,
∴2x+3y=2×5+3×3=19.
故选:A.
9.【解答】解:设上底为xcm,下底为ycm,
根据题意可以列方程组为,
故选:C.
10.【解答】解:设小长方形的长、宽分别为xcm,ycm,
依题意得,
解之得,
∴小长方形的长、宽分别为8cm,2cm,
∴S大长方形=ABBC=14×10=140cm2,
故选:D.
二.填空题(共5小题)
11.【解答】解:设买了x只红笔,y本随意贴,根据题意可得:2x+3y=10,
∵笔和随意贴的数目是整数,
∴x=2,y=2,
答:她买了2支红笔,
故答案为:2.
12.【解答】解:设需要每千克19元的糖果x千克,每千克10元糖果y千克,根据题意可得:,
故答案为:.
13.【解答】解:设一共有x名环卫工人,要发放的口罩共有y个,
依题意,得:,
解得:.
故答案为:8.
14.【解答】解:设长方形纸片的长为x,宽为y,
依题意,得:,
解得:,
∴x﹣y=3,x+2y=6,
∴点A的坐标为(﹣3,6).
故答案为:(﹣3,6).
15.【解答】解:设每个入口每小时可进可容纳人数的x%,每个出口每小时可出可容纳人数的y%,
依题意,得:,
解得:,
∴==.
故答案为:.
三.解答题(共4小题)
16.【解答】解:设三人间租住了x间,两人间租住了y间,
依题意,得:,
解得:.
答:三人间租住了8间,两人间租住了13间.
17.【解答】解:(1)设医用口罩的单价为x元/个,洗手液的单价为y元/瓶,
根据题意得:,
解得:,
答:医用口罩的单价为2.5
元/个,洗手液的单价为30元/瓶;
(2)设增加购买N95口罩a个,洗手液b瓶,则医用口罩(1200﹣a)个,
根据题意得:6a+2.5(1200﹣a)+30b=5400,
化简,得:7a+60b=4800,
∴b=80﹣,
∵a,b都为正整数,
∴a为60的倍数,且a≤200,
∴,,,
∴有三种购买方案.
18.【解答】解:(1)设装运甲种家电的汽车有x辆,装运乙种家电的汽车有y辆,
依题意,得:,
解得:.
答:装运甲种家电的汽车有6辆,装运乙种家电的汽车有2辆.
(2)100×20×6+200×15×2=18000(元).
答:该公司售完这150台家电后的总利润是18000元.
19.【解答】解:(1)由题意得:﹣2a+3a=﹣2b+2a,
则﹣a=﹣2b,
故a=2b.
故答案为:a=2b;
(2)由题意得:﹣2a+2a=b﹣1+(﹣2b),
解得b=﹣1,
由(1)得a=2b,
则a=﹣2.
故答案为:﹣2,﹣1.
