6.5垂直(2)-苏科版七年级数学上册导学案(含部分答案)
文档属性
| 名称 | 6.5垂直(2)-苏科版七年级数学上册导学案(含部分答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 18:01:01 | ||
图片预览



文档简介
课题:6.5垂直(2)
【学习目标】经历“观察、操作----探索、猜想-----推理”的认知过程、感知“垂线段最短”的性质.
【重点难点】“垂线段最短”的性质应用.
【导学指导】:
一、自主学习
1、如图,若要从点A处横穿马路,
怎样走线路最短?
你能把最短的线路画出来吗?
2、你观察过吗?体育课上怎样测量同学们的跳远成绩?
3、如图,线段PA、线段PB、线段PC、线段PD是P点到直线l的最短路线吗?
如果不是,请画出P点到直线a的最短路线,并量出它的长度。
垂线性质二:直线外一点到直线上各点连接的所有线段中,
最短。
我们把直线外一点到这条直线的___________
叫做点P到直线l的距离
二、例题评析:
1.
如图1,BC⊥AB,BC=6cm,AB=8cm,AC=10cm,则点A到BC的距离是
cm,点C到AB的距离是
cm,A、C两点间的距离是
cm.
图1
图2
2.如图,直线a上有一点M,直线b上有一点N,用三角尺画图.
(1)画点M到直线b的最短线段,垂足为点A;
(2)画点N到直线a的最短线段,垂足为点B.
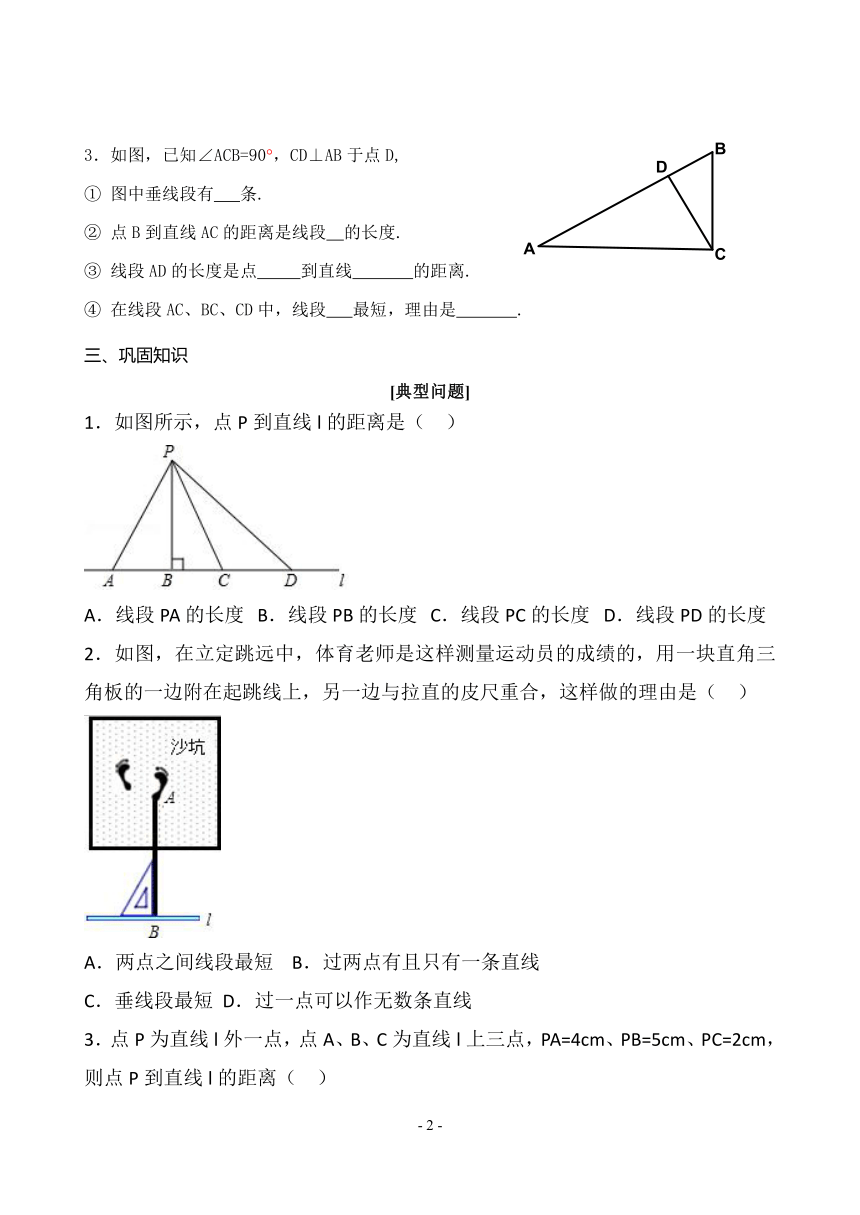
3.如图,已知∠ACB=90°,CD⊥AB于点D,
①
图中垂线段有
条.
②
点B到直线AC的距离是线段
的长度.
③
线段AD的长度是点
到直线
的距离.
④
在线段AC、BC、CD中,线段
最短,理由是
.
三、巩固知识
[典型问题]
1.如图所示,点P到直线l的距离是(
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
2.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是(
)
A.两点之间线段最短
B.过两点有且只有一条直线
C.垂线段最短
D.过一点可以作无数条直线
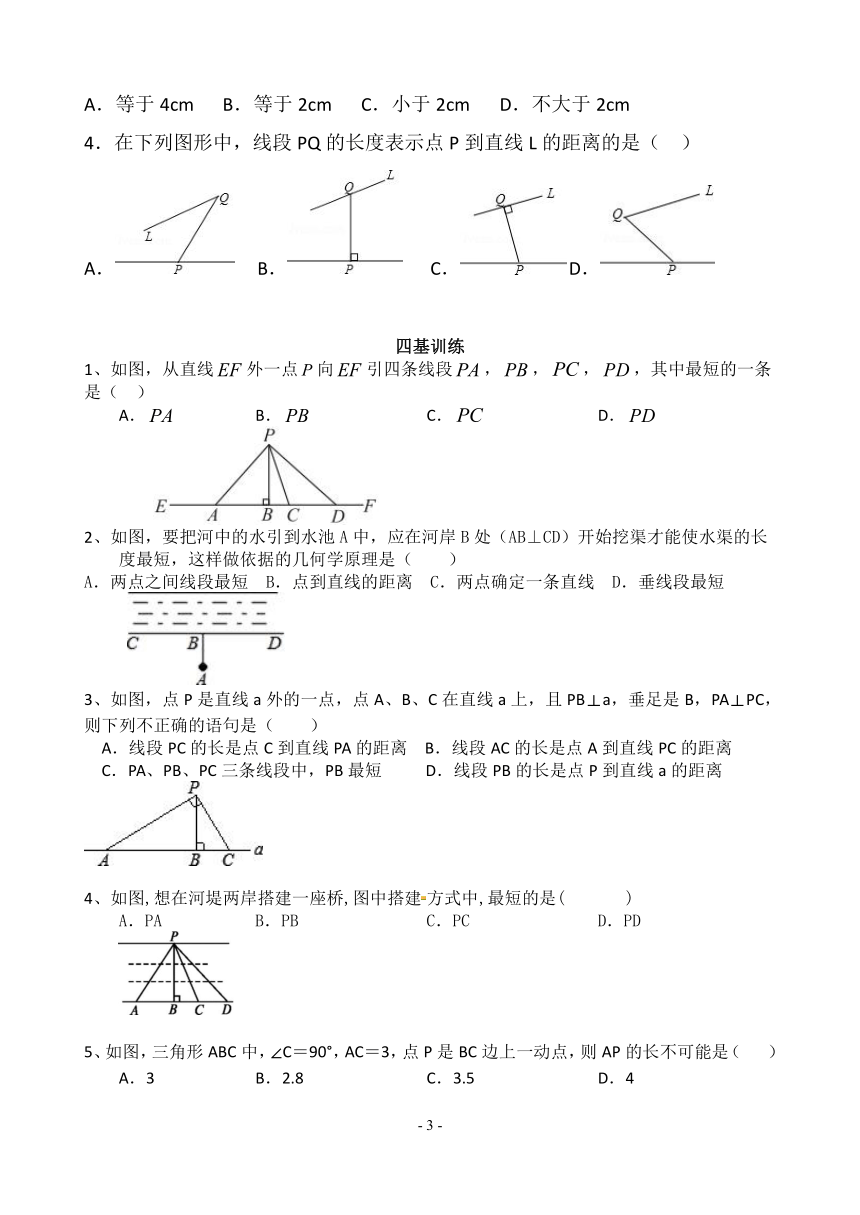
3.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm、PB=5cm、PC=2cm,则点P到直线l的距离(
)
A.等于4cm
B.等于2cm
C.小于2cm
D.不大于2cm
4.在下列图形中,线段PQ的长度表示点P到直线L的距离的是(
)
A.
B.
C.
D.
四基训练
1、如图,从直线外一点向引四条线段,,,,其中最短的一条是(
)
A.
B.
C.
D.
2、如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
3、如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )
A.线段PC的长是点C到直线PA的距离
B.线段AC的长是点A到直线PC的距离
C.PA、PB、PC三条线段中,PB最短
D.线段PB的长是点P到直线a的距离
4、如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是(
)
A.PA
B.PB
C.PC
D.PD
5、如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是(
)
A.3
B.2.8
C.3.5
D.4
6、点在直线外,点在直线上,两点的距离记作,点到直线的距离记作,则与的大小关系是
(
)
A.
B.
C.
D.
7、如图所示,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.
B.
C.
D.
8、如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长
B.线段CD的长
C.线段AD的长
D.线段AB的长
9、点A为直线l外一点,点B在直线l上,若AB=5厘米,则点A到直线l的距离( )
A.大于5厘米
B.等于5厘米
C.小于5厘米
D.不大于5厘米
10、下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B.
C.
D.
11、如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;⑤线段AB是B点到AC的距离.
A.2
B.3
C.4
D.5
12、如图,点A,B,C在直线l上,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是_____cm.
13、如图,AB∥CD,BC∥AD.AC⊥BC于点C,CE⊥AB于点E,那么AB、CD间的距离是___
______的长,BC、AD间的距离是_________的长.
14、如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
拓展提升
15.如图,点A,B在直线m上,点P在直线m外,点Q是直线m上异于点A,B的任意一点,则下列说法或结论正确的是(
)
A.射线AB和射线BA表示同一条射线
B.线段PQ的长度就是点P到直线m的距离
C.连接AP,BP,则AP+BP>AB
D.不论点Q在何处,AQ=AB﹣BQ或AQ=AB+BQ
答案:
一、自主学习
1、如图,若要从点A处横穿马路,
怎样走线路最短?
你能把最短的线路画出来吗?
2、你观察过吗?体育课上怎样测量同学们的跳远成绩?
3、如图,线段PA、线段PB、线段PC、线段PD是P点到直线l的最短路线吗?
如果不是,请画出P点到直线a的最短路线,并量出它的长度。
垂线性质二:直线外一点到直线上各点连接的所有线段中,
垂线段
最短。
我们把直线外一点到这条直线的__垂线段的长度
叫做点P到直线l的距离
二、例题评析:
1.
如图1,BC⊥AB,BC=6cm,AB=8cm,AC=10cm,则点A到BC的距离是
8cm,点C到AB的距离是
6
cm,A、C两点间的距离是
10
cm.
图1
图2
2.如图,直线a上有一点M,直线b上有一点N,用三角尺画图.
(1)画点M到直线b的最短线段,垂足为点A;
(2)画点N到直线a的最短线段,垂足为点B.
3.如图,已知∠ACB=90°,CD⊥AB于点D,
①
图中垂线段有
5
条.
②
点B到直线AC的距离是线段
BC
的长度.
③
线段AD的长度是点
A
到直线
CD
的距离.
④
在线段AC、BC、CD中,线段
CD
最短,理由是
垂线段最短
.
三、巩固知识
[典型问题]
1.如图所示,点P到直线l的距离是(B)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
2.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是(C)
A.两点之间线段最短
B.过两点有且只有一条直线
C.垂线段最短
D.过一点可以作无数条直线
3.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm、PB=5cm、PC=2cm,则点P到直线l的距离(D)
A.等于4cm
B.等于2cm
C.小于2cm
D.不大于2cm
4.在下列图形中,线段PQ的长度表示点P到直线L的距离的是(C)
A.
B.
C.
D.
四基训练
1、如图,从直线外一点向引四条线段,,,,其中最短的一条是(
B
)
A.
B.
C.
D.
2、如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( D )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
3、如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,
则下列不正确的语句是(B )
A.线段PC的长是点C到直线PA的距离
B.线段AC的长是点A到直线PC的距离
C.PA、PB、PC三条线段中,PB最短
D.线段PB的长是点P到直线a的距离
4、如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是(
B
)
A.PA
B.PB
C.PC
D.PD
5、如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是(
B
)
A.3
B.2.8
C.3.5
D.4
6、点在直线外,点在直线上,两点的距离记作,点到直线的距离记作,
则与的大小关系是
(
C
)
A.
B.
C.
D.
7、如图所示,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( C )
A.
B.
C.
D.
8、如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( B )
A.线段CA的长
B.线段CD的长
C.线段AD的长
D.线段AB的长
9、点A为直线l外一点,点B在直线l上,若AB=5厘米,则点A到直线l的距离( D )
A.大于5厘米
B.等于5厘米
C.小于5厘米
D.不大于5厘米
10、下列图形中,线段AD的长表示点A到直线BC距离的是( B )
A.B.
C.
D.
11、如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( A )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;⑤线段AB是B点到AC的距离.
A.2
B.3
C.4
D.5
12、如图,点A,B,C在直线l上,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是__5___cm.
13、如图,AB∥CD,BC∥AD.AC⊥BC于点C,CE⊥AB于点E,那么AB、CD间的距离是___CE
______的长,BC、AD间的距离是___AC______的长.
14、如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
解:
(1)连接AB,沿线段AB走。理由:两点之间,线段最短。
(2)过点B作铁路的垂线BE,垂足为E,沿BE走。理由:垂线段最短。
(3)过点A作河流的垂线AF.垂足为F,沿AF走。理由:垂线段最短。
拓展提升
15.如图,点A,B在直线m上,点P在直线m外,点Q是直线m上异于点A,B的任意一点,则下列说法或结论正确的是(C)
A.射线AB和射线BA表示同一条射线
B.线段PQ的长度就是点P到直线m的距离
C.连接AP,BP,则AP+BP>AB
D.不论点Q在何处,AQ=AB﹣BQ或AQ=AB+BQ
-
2
-
【学习目标】经历“观察、操作----探索、猜想-----推理”的认知过程、感知“垂线段最短”的性质.
【重点难点】“垂线段最短”的性质应用.
【导学指导】:
一、自主学习
1、如图,若要从点A处横穿马路,
怎样走线路最短?
你能把最短的线路画出来吗?
2、你观察过吗?体育课上怎样测量同学们的跳远成绩?
3、如图,线段PA、线段PB、线段PC、线段PD是P点到直线l的最短路线吗?
如果不是,请画出P点到直线a的最短路线,并量出它的长度。
垂线性质二:直线外一点到直线上各点连接的所有线段中,
最短。
我们把直线外一点到这条直线的___________
叫做点P到直线l的距离
二、例题评析:
1.
如图1,BC⊥AB,BC=6cm,AB=8cm,AC=10cm,则点A到BC的距离是
cm,点C到AB的距离是
cm,A、C两点间的距离是
cm.
图1
图2
2.如图,直线a上有一点M,直线b上有一点N,用三角尺画图.
(1)画点M到直线b的最短线段,垂足为点A;
(2)画点N到直线a的最短线段,垂足为点B.
3.如图,已知∠ACB=90°,CD⊥AB于点D,
①
图中垂线段有
条.
②
点B到直线AC的距离是线段
的长度.
③
线段AD的长度是点
到直线
的距离.
④
在线段AC、BC、CD中,线段
最短,理由是
.
三、巩固知识
[典型问题]
1.如图所示,点P到直线l的距离是(
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
2.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是(
)
A.两点之间线段最短
B.过两点有且只有一条直线
C.垂线段最短
D.过一点可以作无数条直线
3.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm、PB=5cm、PC=2cm,则点P到直线l的距离(
)
A.等于4cm
B.等于2cm
C.小于2cm
D.不大于2cm
4.在下列图形中,线段PQ的长度表示点P到直线L的距离的是(
)
A.
B.
C.
D.
四基训练
1、如图,从直线外一点向引四条线段,,,,其中最短的一条是(
)
A.
B.
C.
D.
2、如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
3、如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )
A.线段PC的长是点C到直线PA的距离
B.线段AC的长是点A到直线PC的距离
C.PA、PB、PC三条线段中,PB最短
D.线段PB的长是点P到直线a的距离
4、如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是(
)
A.PA
B.PB
C.PC
D.PD
5、如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是(
)
A.3
B.2.8
C.3.5
D.4
6、点在直线外,点在直线上,两点的距离记作,点到直线的距离记作,则与的大小关系是
(
)
A.
B.
C.
D.
7、如图所示,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.
B.
C.
D.
8、如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长
B.线段CD的长
C.线段AD的长
D.线段AB的长
9、点A为直线l外一点,点B在直线l上,若AB=5厘米,则点A到直线l的距离( )
A.大于5厘米
B.等于5厘米
C.小于5厘米
D.不大于5厘米
10、下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B.
C.
D.
11、如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;⑤线段AB是B点到AC的距离.
A.2
B.3
C.4
D.5
12、如图,点A,B,C在直线l上,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是_____cm.
13、如图,AB∥CD,BC∥AD.AC⊥BC于点C,CE⊥AB于点E,那么AB、CD间的距离是___
______的长,BC、AD间的距离是_________的长.
14、如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
拓展提升
15.如图,点A,B在直线m上,点P在直线m外,点Q是直线m上异于点A,B的任意一点,则下列说法或结论正确的是(
)
A.射线AB和射线BA表示同一条射线
B.线段PQ的长度就是点P到直线m的距离
C.连接AP,BP,则AP+BP>AB
D.不论点Q在何处,AQ=AB﹣BQ或AQ=AB+BQ
答案:
一、自主学习
1、如图,若要从点A处横穿马路,
怎样走线路最短?
你能把最短的线路画出来吗?
2、你观察过吗?体育课上怎样测量同学们的跳远成绩?
3、如图,线段PA、线段PB、线段PC、线段PD是P点到直线l的最短路线吗?
如果不是,请画出P点到直线a的最短路线,并量出它的长度。
垂线性质二:直线外一点到直线上各点连接的所有线段中,
垂线段
最短。
我们把直线外一点到这条直线的__垂线段的长度
叫做点P到直线l的距离
二、例题评析:
1.
如图1,BC⊥AB,BC=6cm,AB=8cm,AC=10cm,则点A到BC的距离是
8cm,点C到AB的距离是
6
cm,A、C两点间的距离是
10
cm.
图1
图2
2.如图,直线a上有一点M,直线b上有一点N,用三角尺画图.
(1)画点M到直线b的最短线段,垂足为点A;
(2)画点N到直线a的最短线段,垂足为点B.
3.如图,已知∠ACB=90°,CD⊥AB于点D,
①
图中垂线段有
5
条.
②
点B到直线AC的距离是线段
BC
的长度.
③
线段AD的长度是点
A
到直线
CD
的距离.
④
在线段AC、BC、CD中,线段
CD
最短,理由是
垂线段最短
.
三、巩固知识
[典型问题]
1.如图所示,点P到直线l的距离是(B)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
2.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是(C)
A.两点之间线段最短
B.过两点有且只有一条直线
C.垂线段最短
D.过一点可以作无数条直线
3.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm、PB=5cm、PC=2cm,则点P到直线l的距离(D)
A.等于4cm
B.等于2cm
C.小于2cm
D.不大于2cm
4.在下列图形中,线段PQ的长度表示点P到直线L的距离的是(C)
A.
B.
C.
D.
四基训练
1、如图,从直线外一点向引四条线段,,,,其中最短的一条是(
B
)
A.
B.
C.
D.
2、如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( D )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
3、如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,
则下列不正确的语句是(B )
A.线段PC的长是点C到直线PA的距离
B.线段AC的长是点A到直线PC的距离
C.PA、PB、PC三条线段中,PB最短
D.线段PB的长是点P到直线a的距离
4、如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是(
B
)
A.PA
B.PB
C.PC
D.PD
5、如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是(
B
)
A.3
B.2.8
C.3.5
D.4
6、点在直线外,点在直线上,两点的距离记作,点到直线的距离记作,
则与的大小关系是
(
C
)
A.
B.
C.
D.
7、如图所示,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( C )
A.
B.
C.
D.
8、如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( B )
A.线段CA的长
B.线段CD的长
C.线段AD的长
D.线段AB的长
9、点A为直线l外一点,点B在直线l上,若AB=5厘米,则点A到直线l的距离( D )
A.大于5厘米
B.等于5厘米
C.小于5厘米
D.不大于5厘米
10、下列图形中,线段AD的长表示点A到直线BC距离的是( B )
A.B.
C.
D.
11、如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( A )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;⑤线段AB是B点到AC的距离.
A.2
B.3
C.4
D.5
12、如图,点A,B,C在直线l上,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是__5___cm.
13、如图,AB∥CD,BC∥AD.AC⊥BC于点C,CE⊥AB于点E,那么AB、CD间的距离是___CE
______的长,BC、AD间的距离是___AC______的长.
14、如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
解:
(1)连接AB,沿线段AB走。理由:两点之间,线段最短。
(2)过点B作铁路的垂线BE,垂足为E,沿BE走。理由:垂线段最短。
(3)过点A作河流的垂线AF.垂足为F,沿AF走。理由:垂线段最短。
拓展提升
15.如图,点A,B在直线m上,点P在直线m外,点Q是直线m上异于点A,B的任意一点,则下列说法或结论正确的是(C)
A.射线AB和射线BA表示同一条射线
B.线段PQ的长度就是点P到直线m的距离
C.连接AP,BP,则AP+BP>AB
D.不论点Q在何处,AQ=AB﹣BQ或AQ=AB+BQ
-
2
-
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
