北师大版七年级数学下册 1.5 平方差公式 同步测试题 (word版 含解析)
文档属性
| 名称 | 北师大版七年级数学下册 1.5 平方差公式 同步测试题 (word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 69.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 14:57:26 | ||
图片预览




文档简介
1.5
平方差公式
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
若,,则(?
?
?
?
)
A.
B.
C.
D.
?
2.
已知,,则(?
?
?
?
)
A.
B.
C.
D.
?
3.
为了美化城市,经统一规划,将一正方形草坪的南北方向增加,东西方向缩短,则改造后的长方形草坪面积与原来正方形草坪面积相比(
)
A.增加
B.减少
C.增加
D.减少
?
4.
的计算结果是(
)
A.
B.
C.
D.
?
5.
下列各式中,与相等的是(
)
A.
B.
C.
D.
?
6.
下列各式中,能运用平方差公式进行计算的是(
)
A.
B.
C.
D.
?
7.
…计算结果的个位数字是(
)
A.
B.
C.
D.
?
8.
下列各式中,能用平方差公式计算的是(
)
A.
B.
C.
D.
?9.
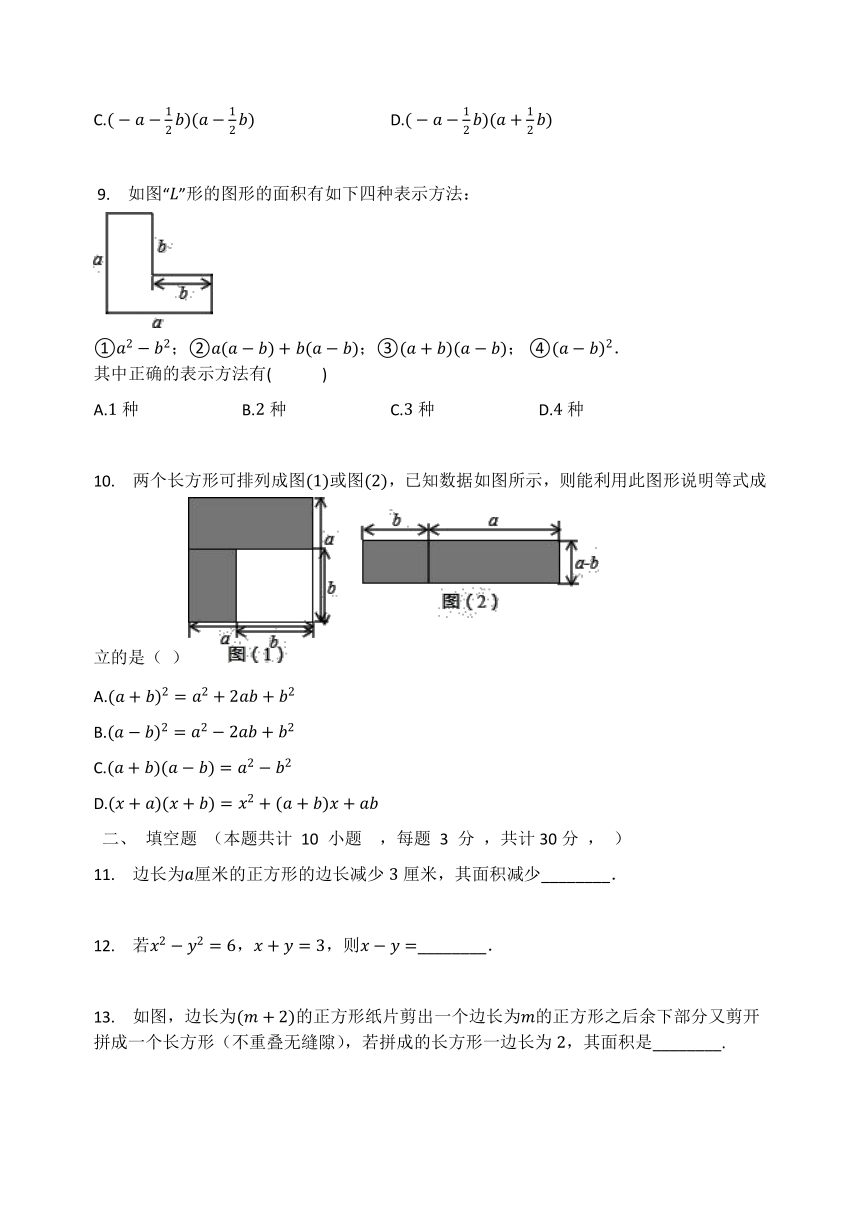
如图“”形的图形的面积有如下四种表示方法:
①;②;③;?④.
其中正确的表示方法有(?
?
?
?
)
A.种
B.种
C.种
D.种
?
10.
两个长方形可排列成图或图,已知数据如图所示,则能利用此图形说明等式成立的是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
边长为厘米的正方形的边长减少厘米,其面积减少________.
?
12.
若,,则________.
?
13.
如图,边长为的正方形纸片剪出一个边长为的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为,其面积是________.
?14.
计算:=________.
?
15.
已知:,那么________.
?
16.
________.
?
17.
已知,,则________.
?
18.
计算:??________.?
?
19.
如图,边长为的正方形纸片剪出一个边长为的正方形之后,剩余部分可剪拼成一个长方形,若该长方形一边的长为,则另一边的长为________.
?
20.
如图,在边长为的正方形中挖掉一个边长为的正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)面积,验证了一个等式,此等式是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
用简便方法计算:
(1).
(2)
?
22.
计算:.
?
23.
(1)观察下列各式:,,…你发现了什么规律?试用你发现的规律填空:________,________.
(2)请你用含一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性.
?
24.
如图,在边长为的正方形的一角是一个边长为的正方形,请用这个图形验证公式:.
?
25.
观察下列不等式:
…
(1)用含有字母(的整数)的等式表示这一规律;?
(2)请用所学知识验证这个规律的正确性;
(3)借助你发现的规律把写成两个正整数的平方差的形式:
.
?
26.
从边长为的正方形中剪掉一个边长为的正方形(如图),然后将剩余部分拼成一个长方形(如图).
上述操作能验证的等式是;(请选择正确的一个)
、,
、?,
、.
应用你从选出的等式,完成下列各题:
①已知,,求的值.
②计算:.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:因为,
,,
所以,
所以.
故选.
2.
【答案】
C
【解答】
解:∵
,,
∴
原式,
故选.
3.
【答案】
D
【解答】
解:设原来的正方形边长为米,则原来的面积为平方米,
改造后的长方形草坪面积为(平方米),
改造后的长方形草坪面积与原来正方形草坪面积相比,
所以改造后的长方形草坪面积比原来正方形草坪面积减小了.
故选:.
4.
【答案】
C
【解答】
解:
.
.故选
5.
【答案】
A
【解答】
解:原式.
故选:.
6.
【答案】
B
【解答】
解:能运用平方差公式进行计算的是,
故选
7.
【答案】
B
【解答】
解:原式…
…
;
∵
,,,,个位数按照,,,依次循环,
而,
∴
原式的个位数为.
故选.
8.
【答案】
C
【解答】
解:、两项相同,不符合平方差公式;
、两项都不相同,不符合平方差公式;
、中的两项都是一项完全相同,另一项互为相反数,符合平方差公式.
故选.
9.
【答案】
C
【解答】
解:如图①,
图①中,大正方形面积为,小正方形面积为,
所以整个图形的面积为;
如图②,
一个矩形的面积是,另一个矩形的面积是,
所以整个图形的面积为;
如图③,
在图③中,拼成一长方形,长为,宽为,则面积为.
综上所知:矩形的面积为①;②;③共种方法正确.
故选.
10.
【答案】
C
【解答】
解:图中,阴影部分的面积是,
图的面积是,
则能利用此图形说明等式成立的是:.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:边长为厘米的正方形的面积为:;
边长为厘米的正方形的面积为:,
则面积减小.
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
,
故答案为:.
13.
【答案】
【解答】
解:依题意得剩余部分为
,
而拼成的矩形一边长为,
∴
另一边长是.
∴
面积为.
故答案为:
14.
【答案】
【解答】
=.
15.
【答案】
【解答】
解:∵
,
∴
,即.
故答案为:.
16.
【答案】
【解答】
解:原式.
故答案为:.
17.
【答案】
【解答】
解:∵
,,
∴
原式,
故答案为:
18.
【答案】
【解答】
解:原式
.
故答案为:.
19.
【答案】
【解答】
设另一边长为,
根据题意得,=,
∴
=
20.
【答案】
【解答】
解:左边图形中阴影部分的面积是,右边图形中阴影部分的面积是,根据阴影部分的面积相等得:.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
=
=
=;
=
=
=.
【解答】
=
=
=;
=
=
=.
22.
【答案】
解:原式
.
【解答】
解:原式
.
23.
【答案】
,
(2)可以得出规律:,
左边右边.
【解答】
解:(1)由,界于和之间的正整数,
,界于和之间的正整数,
,界于和之间的正整数,
∴
试着推出:,界于和之间的正整数,且左边右边成立,
,界于和之间的正整数,且左边右边成立,
(2)可以得出规律:,
左边右边.
24.
【答案】
解:由图可知:大正方形的面积-小正方形的面积剩余部分的面积,
∴
,即.
【解答】
解:由图可知:大正方形的面积-小正方形的面积剩余部分的面积,
∴
,即.
25.
【答案】
解:(1)根据题意得:(的整数);
(2)左边右边,
则(的整数);
(3).
【解答】
解:(1)根据题意得:(的整数);
(2)左边右边,
则(的整数);
(3).
26.
【答案】
解:根据图形得:,
上述操作能验证的等式是.
故答案为:.
①∵
,
,
∴
;
②原式
.
【解答】
解:根据图形得:,
上述操作能验证的等式是.
故答案为:.
①∵
,
,
∴
;
②原式
.
平方差公式
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
若,,则(?
?
?
?
)
A.
B.
C.
D.
?
2.
已知,,则(?
?
?
?
)
A.
B.
C.
D.
?
3.
为了美化城市,经统一规划,将一正方形草坪的南北方向增加,东西方向缩短,则改造后的长方形草坪面积与原来正方形草坪面积相比(
)
A.增加
B.减少
C.增加
D.减少
?
4.
的计算结果是(
)
A.
B.
C.
D.
?
5.
下列各式中,与相等的是(
)
A.
B.
C.
D.
?
6.
下列各式中,能运用平方差公式进行计算的是(
)
A.
B.
C.
D.
?
7.
…计算结果的个位数字是(
)
A.
B.
C.
D.
?
8.
下列各式中,能用平方差公式计算的是(
)
A.
B.
C.
D.
?9.
如图“”形的图形的面积有如下四种表示方法:
①;②;③;?④.
其中正确的表示方法有(?
?
?
?
)
A.种
B.种
C.种
D.种
?
10.
两个长方形可排列成图或图,已知数据如图所示,则能利用此图形说明等式成立的是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
边长为厘米的正方形的边长减少厘米,其面积减少________.
?
12.
若,,则________.
?
13.
如图,边长为的正方形纸片剪出一个边长为的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为,其面积是________.
?14.
计算:=________.
?
15.
已知:,那么________.
?
16.
________.
?
17.
已知,,则________.
?
18.
计算:??________.?
?
19.
如图,边长为的正方形纸片剪出一个边长为的正方形之后,剩余部分可剪拼成一个长方形,若该长方形一边的长为,则另一边的长为________.
?
20.
如图,在边长为的正方形中挖掉一个边长为的正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)面积,验证了一个等式,此等式是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
用简便方法计算:
(1).
(2)
?
22.
计算:.
?
23.
(1)观察下列各式:,,…你发现了什么规律?试用你发现的规律填空:________,________.
(2)请你用含一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性.
?
24.
如图,在边长为的正方形的一角是一个边长为的正方形,请用这个图形验证公式:.
?
25.
观察下列不等式:
…
(1)用含有字母(的整数)的等式表示这一规律;?
(2)请用所学知识验证这个规律的正确性;
(3)借助你发现的规律把写成两个正整数的平方差的形式:
.
?
26.
从边长为的正方形中剪掉一个边长为的正方形(如图),然后将剩余部分拼成一个长方形(如图).
上述操作能验证的等式是;(请选择正确的一个)
、,
、?,
、.
应用你从选出的等式,完成下列各题:
①已知,,求的值.
②计算:.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:因为,
,,
所以,
所以.
故选.
2.
【答案】
C
【解答】
解:∵
,,
∴
原式,
故选.
3.
【答案】
D
【解答】
解:设原来的正方形边长为米,则原来的面积为平方米,
改造后的长方形草坪面积为(平方米),
改造后的长方形草坪面积与原来正方形草坪面积相比,
所以改造后的长方形草坪面积比原来正方形草坪面积减小了.
故选:.
4.
【答案】
C
【解答】
解:
.
.故选
5.
【答案】
A
【解答】
解:原式.
故选:.
6.
【答案】
B
【解答】
解:能运用平方差公式进行计算的是,
故选
7.
【答案】
B
【解答】
解:原式…
…
;
∵
,,,,个位数按照,,,依次循环,
而,
∴
原式的个位数为.
故选.
8.
【答案】
C
【解答】
解:、两项相同,不符合平方差公式;
、两项都不相同,不符合平方差公式;
、中的两项都是一项完全相同,另一项互为相反数,符合平方差公式.
故选.
9.
【答案】
C
【解答】
解:如图①,
图①中,大正方形面积为,小正方形面积为,
所以整个图形的面积为;
如图②,
一个矩形的面积是,另一个矩形的面积是,
所以整个图形的面积为;
如图③,
在图③中,拼成一长方形,长为,宽为,则面积为.
综上所知:矩形的面积为①;②;③共种方法正确.
故选.
10.
【答案】
C
【解答】
解:图中,阴影部分的面积是,
图的面积是,
则能利用此图形说明等式成立的是:.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:边长为厘米的正方形的面积为:;
边长为厘米的正方形的面积为:,
则面积减小.
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
,
故答案为:.
13.
【答案】
【解答】
解:依题意得剩余部分为
,
而拼成的矩形一边长为,
∴
另一边长是.
∴
面积为.
故答案为:
14.
【答案】
【解答】
=.
15.
【答案】
【解答】
解:∵
,
∴
,即.
故答案为:.
16.
【答案】
【解答】
解:原式.
故答案为:.
17.
【答案】
【解答】
解:∵
,,
∴
原式,
故答案为:
18.
【答案】
【解答】
解:原式
.
故答案为:.
19.
【答案】
【解答】
设另一边长为,
根据题意得,=,
∴
=
20.
【答案】
【解答】
解:左边图形中阴影部分的面积是,右边图形中阴影部分的面积是,根据阴影部分的面积相等得:.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
=
=
=;
=
=
=.
【解答】
=
=
=;
=
=
=.
22.
【答案】
解:原式
.
【解答】
解:原式
.
23.
【答案】
,
(2)可以得出规律:,
左边右边.
【解答】
解:(1)由,界于和之间的正整数,
,界于和之间的正整数,
,界于和之间的正整数,
∴
试着推出:,界于和之间的正整数,且左边右边成立,
,界于和之间的正整数,且左边右边成立,
(2)可以得出规律:,
左边右边.
24.
【答案】
解:由图可知:大正方形的面积-小正方形的面积剩余部分的面积,
∴
,即.
【解答】
解:由图可知:大正方形的面积-小正方形的面积剩余部分的面积,
∴
,即.
25.
【答案】
解:(1)根据题意得:(的整数);
(2)左边右边,
则(的整数);
(3).
【解答】
解:(1)根据题意得:(的整数);
(2)左边右边,
则(的整数);
(3).
26.
【答案】
解:根据图形得:,
上述操作能验证的等式是.
故答案为:.
①∵
,
,
∴
;
②原式
.
【解答】
解:根据图形得:,
上述操作能验证的等式是.
故答案为:.
①∵
,
,
∴
;
②原式
.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
