鲁教版(五四制)八年级数学上册 第4章图形的平移与旋转达标检测(word版 含答案)
文档属性
| 名称 | 鲁教版(五四制)八年级数学上册 第4章图形的平移与旋转达标检测(word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 688.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 20:10:58 | ||
图片预览

文档简介
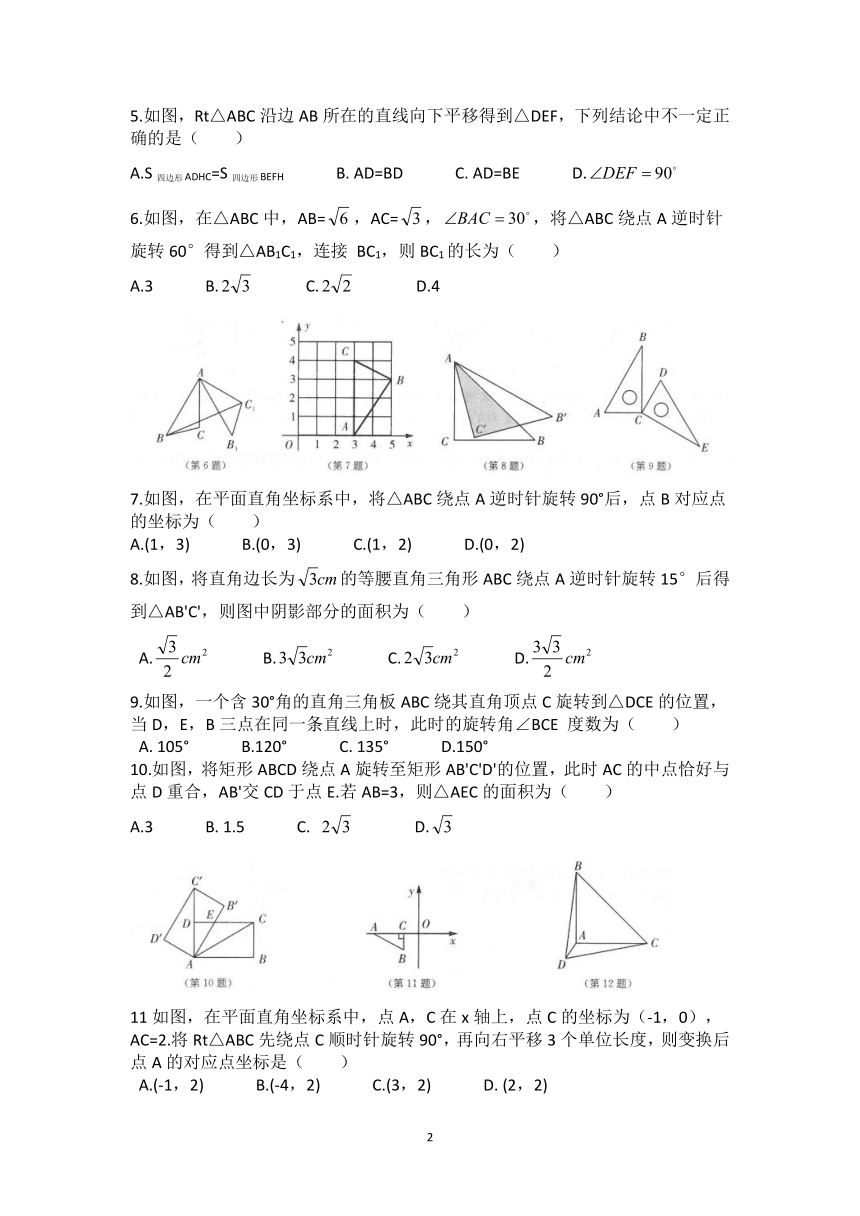
第四章达标测试卷
时间:60分钟
满分:100分
得分
一、选择题(本题包括12小题每小题3分,共36分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是(
)
2.在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以将图形
进行以下的操作(
)
A.先逆时针旋转90°,再向左平移
B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移
D.先顺时针旋转90°,再向右平移
3.如图,在同一平面内,将△ABC绕点A逆时针旋转到△ADE的位置,若AC⊥
DE,,则的度数为(
)
A.56°
B.
44°
C.
34°
D.40°
4.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再把△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,则点A的对应点A2的坐标是(
)
A.(5,2)
B.(1,0)
C.(3,-1)
D.(5,-2)
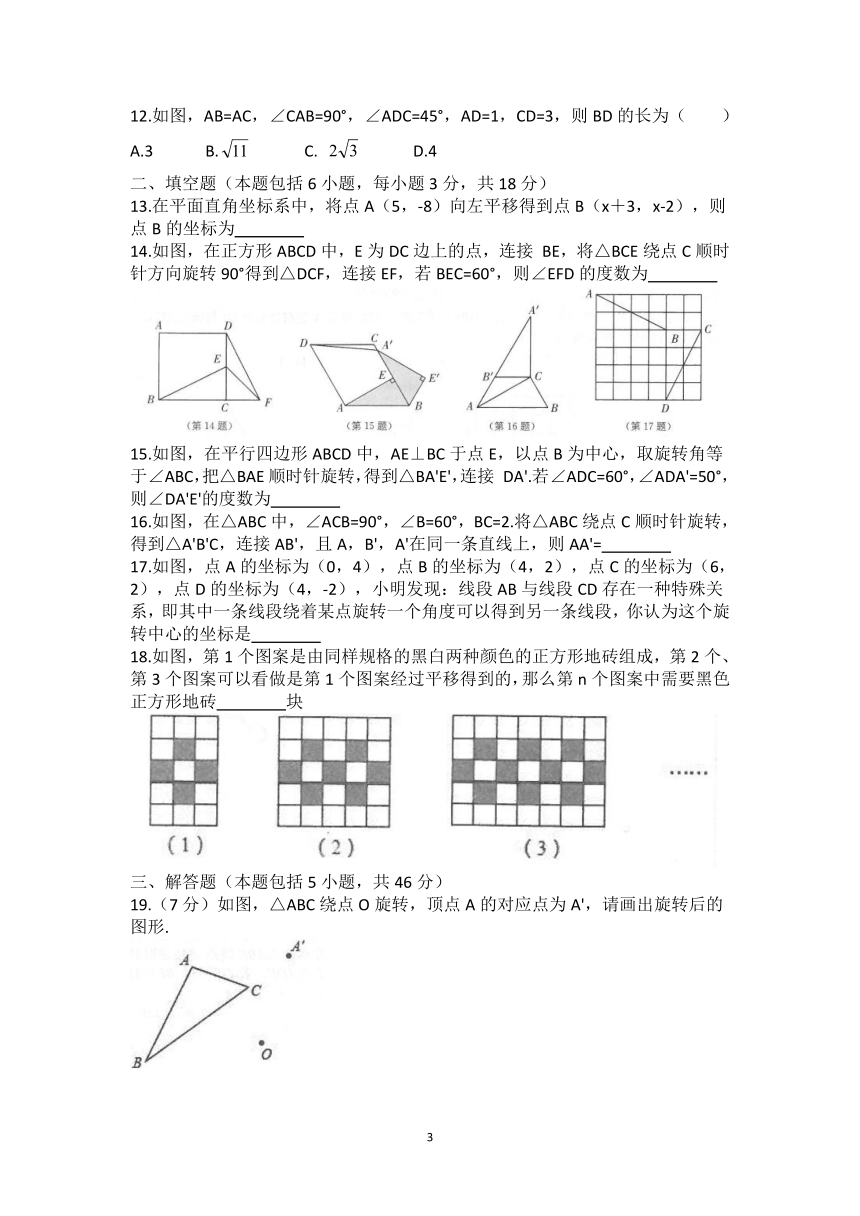
5.如图,Rt△ABC沿边AB所在的直线向下平移得到△DEF,下列结论中不一定正确的是(
)
A.S四边形ADHC=S四边形BEFH
B.
AD=BD
C.
AD=BE
D.
6.如图,在△ABC中,AB=,AC=,,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接
BC1,则BC1的长为(
)
A.3
B.
C.
D.4
7.如图,在平面直角坐标系中,将△ABC绕点A逆时针旋转90°后,点B对应点的坐标为(
)
A.(1,3)
B.(0,3)
C.(1,2)
D.(0,2)
8.如图,将直角边长为的等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB'C',则图中阴影部分的面积为(
)
A.
B.
C.
D.
9.如图,一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D,E,B三点在同一条直线上时,此时的旋转角∠BCE
度数为(
)
A.
105°
B.120°
C.
135°
D.150°
10.如图,将矩形ABCD绕点A旋转至矩形AB'C'D'的位置,此时AC的中点恰好与点D重合,AB'交CD于点E.若AB=3,则△AEC的面积为(
)
A.3
B.
1.5
C.
D.
11如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是(
)
A.(-1,2)
B.(-4,2)
C.(3,2)
D.
(2,2)
12.如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=1,CD=3,则BD的长为(
)
A.3
B.
C.
D.4
二、填空题(本题包括6小题,每小题3分,共18分)
13.在平面直角坐标系中,将点A(5,-8)向左平移得到点B(x+3,x-2),则点B的坐标为
14.如图,在正方形ABCD中,E为DC边上的点,连接
BE,将△BCE绕点C顺时
针方向旋转90°得到△DCF,连接EF,若BEC=60°,则∠EFD的度数为
15.如图,在平行四边形ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA'E',连接
DA'.若∠ADC=60°,∠ADA'=50°,则∠DA'E'的度数为
16.如图,在△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转,得到△A'B'C,连接AB',且A,B',A'在同一条直线上,则AA'=
17.如图,点A的坐标为(0,4),点B的坐标为(4,2),点C的坐标为(6,2),点D的坐标为(4,-2),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是
18.如图,第1个图案是由同样规格的黑白两种颜色的正方形地砖组成,第2个、第3个图案可以看做是第1个图案经过平移得到的,那么第n个图案中需要黑色正方形地砖
块
三、解答题(本题包括5小题,共46分)
19.(7分)如图,△ABC绕点O旋转,顶点A的对应点为A',请画出旋转后的图形.
20.(8分)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,且∠ACB=20°,求∠CAE及∠B的度数.
20.(9分)如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE//BC;
(2)若AB=8,BD=7,求△ADE的周长.
21.(10分)如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B1C2.
22.(12分)如图,在等腰直角三角形ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP=时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A,C重合),求证:2PB2=PA2+PC2.
参考答案
一、选择题
1-5AACAB
6-10ADABD
11-12AB
二、填空题
13、(-3,8)
14、15°
15、160°
16、6
17、(2,0)或(5,3)
18、3n+1
三、解答题
19.
20.根据旋转的性质可知CA=CE,且∠ACE=90°,
所以△ACE是等腰直角三角形
所以∠CAE=45°
根据旋转的可得∠BDC=90°,
∵∠ACB=20°,∴∠ACD=70°
∴∠EDC=115°
∴∠B=∠EDC=115°
21.(1)如图,△A1B1C1为所作。
(2)如图,△A2B2C2为所作。
22.(1)∵△ABC是等腰直角三角形,
∴∠A=∠ACB=45°,
∵△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
∴△ABP≌△CBQ,
∴∠A=∠ACB=∠BCQ=45°,
∴∠PCQ=∠ACB+∠BCQ=45°+45°=90°;
(2)在等腰直角三角形ABC中,
∵AB=4,∴AC=,∵AP=,
∴PC=AC-AP=,
由(1)知,△ABP≌△CBQ,∴CQ=AP=,
由(1)知,∠PCQ=90°,根据勾股定理得,;
(3)证明∶由(1)知,△ABP≌△CBQ,
∴∠ABP=∠CBQ,AP=CQ,PB=BQ
.
∴∠CBQ+∠PBC=∠ABP+∠PBC=90°,
∴△BPQ是等腰直角三角形,△PCQ是直角三角形,
∴PQ=PB,∴AP=CQ,
在Rt△PCQ中,根据勾股定理得,
PQ2=PC2+CQ2=PA2+PC2
∴2PB2=PA2+PC2.
时间:60分钟
满分:100分
得分
一、选择题(本题包括12小题每小题3分,共36分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是(
)
2.在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以将图形
进行以下的操作(
)
A.先逆时针旋转90°,再向左平移
B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移
D.先顺时针旋转90°,再向右平移
3.如图,在同一平面内,将△ABC绕点A逆时针旋转到△ADE的位置,若AC⊥
DE,,则的度数为(
)
A.56°
B.
44°
C.
34°
D.40°
4.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再把△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,则点A的对应点A2的坐标是(
)
A.(5,2)
B.(1,0)
C.(3,-1)
D.(5,-2)
5.如图,Rt△ABC沿边AB所在的直线向下平移得到△DEF,下列结论中不一定正确的是(
)
A.S四边形ADHC=S四边形BEFH
B.
AD=BD
C.
AD=BE
D.
6.如图,在△ABC中,AB=,AC=,,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接
BC1,则BC1的长为(
)
A.3
B.
C.
D.4
7.如图,在平面直角坐标系中,将△ABC绕点A逆时针旋转90°后,点B对应点的坐标为(
)
A.(1,3)
B.(0,3)
C.(1,2)
D.(0,2)
8.如图,将直角边长为的等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB'C',则图中阴影部分的面积为(
)
A.
B.
C.
D.
9.如图,一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D,E,B三点在同一条直线上时,此时的旋转角∠BCE
度数为(
)
A.
105°
B.120°
C.
135°
D.150°
10.如图,将矩形ABCD绕点A旋转至矩形AB'C'D'的位置,此时AC的中点恰好与点D重合,AB'交CD于点E.若AB=3,则△AEC的面积为(
)
A.3
B.
1.5
C.
D.
11如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是(
)
A.(-1,2)
B.(-4,2)
C.(3,2)
D.
(2,2)
12.如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=1,CD=3,则BD的长为(
)
A.3
B.
C.
D.4
二、填空题(本题包括6小题,每小题3分,共18分)
13.在平面直角坐标系中,将点A(5,-8)向左平移得到点B(x+3,x-2),则点B的坐标为
14.如图,在正方形ABCD中,E为DC边上的点,连接
BE,将△BCE绕点C顺时
针方向旋转90°得到△DCF,连接EF,若BEC=60°,则∠EFD的度数为
15.如图,在平行四边形ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA'E',连接
DA'.若∠ADC=60°,∠ADA'=50°,则∠DA'E'的度数为
16.如图,在△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转,得到△A'B'C,连接AB',且A,B',A'在同一条直线上,则AA'=
17.如图,点A的坐标为(0,4),点B的坐标为(4,2),点C的坐标为(6,2),点D的坐标为(4,-2),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是
18.如图,第1个图案是由同样规格的黑白两种颜色的正方形地砖组成,第2个、第3个图案可以看做是第1个图案经过平移得到的,那么第n个图案中需要黑色正方形地砖
块
三、解答题(本题包括5小题,共46分)
19.(7分)如图,△ABC绕点O旋转,顶点A的对应点为A',请画出旋转后的图形.
20.(8分)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,且∠ACB=20°,求∠CAE及∠B的度数.
20.(9分)如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE//BC;
(2)若AB=8,BD=7,求△ADE的周长.
21.(10分)如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B1C2.
22.(12分)如图,在等腰直角三角形ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP=时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A,C重合),求证:2PB2=PA2+PC2.
参考答案
一、选择题
1-5AACAB
6-10ADABD
11-12AB
二、填空题
13、(-3,8)
14、15°
15、160°
16、6
17、(2,0)或(5,3)
18、3n+1
三、解答题
19.
20.根据旋转的性质可知CA=CE,且∠ACE=90°,
所以△ACE是等腰直角三角形
所以∠CAE=45°
根据旋转的可得∠BDC=90°,
∵∠ACB=20°,∴∠ACD=70°
∴∠EDC=115°
∴∠B=∠EDC=115°
21.(1)如图,△A1B1C1为所作。
(2)如图,△A2B2C2为所作。
22.(1)∵△ABC是等腰直角三角形,
∴∠A=∠ACB=45°,
∵△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
∴△ABP≌△CBQ,
∴∠A=∠ACB=∠BCQ=45°,
∴∠PCQ=∠ACB+∠BCQ=45°+45°=90°;
(2)在等腰直角三角形ABC中,
∵AB=4,∴AC=,∵AP=,
∴PC=AC-AP=,
由(1)知,△ABP≌△CBQ,∴CQ=AP=,
由(1)知,∠PCQ=90°,根据勾股定理得,;
(3)证明∶由(1)知,△ABP≌△CBQ,
∴∠ABP=∠CBQ,AP=CQ,PB=BQ
.
∴∠CBQ+∠PBC=∠ABP+∠PBC=90°,
∴△BPQ是等腰直角三角形,△PCQ是直角三角形,
∴PQ=PB,∴AP=CQ,
在Rt△PCQ中,根据勾股定理得,
PQ2=PC2+CQ2=PA2+PC2
∴2PB2=PA2+PC2.
