沪教版(上海市)九年级第二学期专题复习七:直线与圆、圆与圆的位置关系分类讨论(word版,无答案)
文档属性
| 名称 | 沪教版(上海市)九年级第二学期专题复习七:直线与圆、圆与圆的位置关系分类讨论(word版,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 758.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览



文档简介
专题复习七
直线与圆、圆与圆的位置关系分类讨论
知识梳理,
直线与圆、圆与圆的位置关系是上海中考模拟卷及中考卷压轴题中的“常客”,由于牵涉到的条件较多,情况较为复杂,若没有掌握--定的解题规律和方法是很难快速求解的.直线与圆相切的充要条件是d=
r,其中d表示圆心到直线的距离,r表示圆的半径.而圆与圆相切含有两种情况,即圆与圆外切、圆与圆内切,它们的充要条件分别为d=
R+r和d
=|Rr|.其中d表示两圆的圆心距,R和r分别表示两圆的半径.此类问题的求解方法规律性甚强,第一步:列出二或三条件(d,
R,
r),第二步:根据题意列出方程并求解(d=r,
d=
R+r,
d
=|R-r|),第三步:检验解是否存在.掌握以上步骤不必画圆,按部就班便能顺利求解.
典型例题,
[例1]如图,已知:在△ABC中,
AB=AC=5,
BC=6,点D为BC边上一动点(不与B点重合),过点D作射线DE交AB边于点E,使∠BDE=∠A,以D为圆心,DC长为半径作?D.
(1)设BD=x,
AE=y,求y关于x的函数关系,并写出定义域;
(2)当?D与AB边相切时,求BD的长;
(3)如果?E是以E为圆心,
AE长为半径的圆,那么当BD为多少时,
?D与?E相切?
[思路分析]第(2)题是直线
与圆相切,根据题意列出D到AB的距离d,r=
CD为己知,若?D与AB边相切,则d=
r建立方程,求解检验便可.第(3)题根据题意列出D,
E两点的距离d,r=
CD,
R=
AE,若OD与OE相切,依据d=R+r或d
=|R-r|建立方程,求解检验便可.
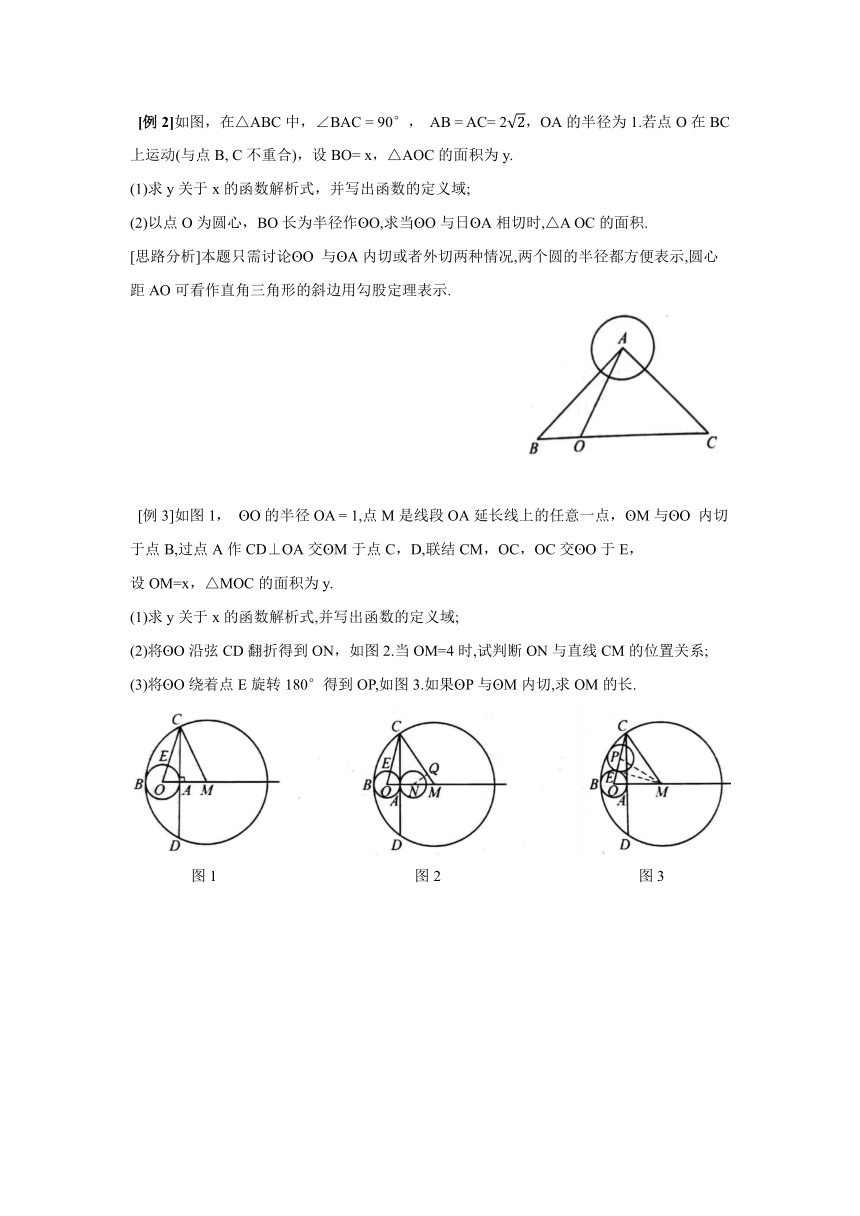
[例2]如图,在△ABC中,∠BAC
=
90°,
AB
=
AC=
2,OA的半径为1.若点O在BC上运动(与点B,
C不重合),设BO=
x,△AOC的面积为y.
(1)求y关于x的函数解析式,并写出函数的定义域;
(2)以点O为圆心,BO长为半径作?O,求当?O与日?A相切时,△A
OC的面积.
[思路分析]本题只需讨论?O
与?A内切或者外切两种情况,两个圆的半径都方便表示,圆心距AO可看作直角三角形的斜边用勾股定理表示.
[例3]如图1,
?O的半径OA
=
1,点M是线段OA延长线上的任意一点,?M与?O
内切于点B,过点A作CD⊥OA交?M于点C,D,联结CM,OC,OC交?O于E,
设OM=x,△MOC的面积为y.
(1)求y关于x的函数解析式,并写出函数的定义域;
(2)将?O沿弦CD翻折得到ON,如图2.当OM=4时,试判断ON与直线CM的位置关系;
(3)将?O绕着点E旋转180°得到OP,如图3.如果?P与?M内切,求OM的长.
图1
图2
图3
练习题
1.如图,已知在直角梯形ABCD中,AB
//
CD,∠C=90°,CD=9,
BC=3,
tan∠A=。
P,
Q分别是边AB,CD上的动点(点P不与点A,点B重合),且有BP
=
2CQ.
(1)求AB的长;
(2)若以C为圆心、CQ为半径作?C,以P为圆心、以PA的长为半径作?P.当?C与?P外切时,试判断四边形PADQ是什么四边形,并说明理由.
2.在梯形ABCD中,∠ABC=90°,AD//BC,AB=8cm,BC=18cm,sin∠BCD=
,点P从点B开始沿BC边向终点C以每秒3
cm的速度移动,点Q从点D开始沿DA边向终点A以每秒2cm的速度移动,设运动时间为t(s).
(1)如图
(a)
,若四边形ABPQ是矩形,求t的值;
(2)若题设中的“BC=18cm”改变为“BC=kcm”,其他条件都不变,要使四边形PCDQ是等腰梯形,求t与k的函数关系式,并写出k的取值范围;
(3)如图
(b)
,如果?P的半径为6
cm,
?Q的半径为4
cm,在移动的过程中,试探索:t为何值时?P与?Q外离、外切、相交?
3.已知:如图,在Rt?ABC中,∠ACB
=
90°,
tan∠ABC
=,AB=5,
D是线段AB上的一点(与点A,
B不重合),直线DP⊥AB,与线段AC相交于点Q,与射线BC相交于点P,E是AQ的中点,线段ED的延长线与线段CB的延长线相交于点F.
(1)求证:△FBD
△FDP;
(2)求BF:
BP的值;
(3)若?A与直线BC相切,
?B的半径等于线段BF的长,设BD=x,当?A与?B相切时,请求出x的值.
4.如图,已知在矩形ABCD中,AB=3,
BC=4,
P是边BC延长线上的一点,联结AP交边CD于点E,把射线AP沿直线AD翻折,交射线CD于点Q,设CP=x,
DQ=y.
(1)求y关于x的函数解析式,并写出定义域.
(2)当以4为半径的OQ与直线AP相切,且?
A与?
Q也相切时,求?
A的半径.
5.如图(a)在矩形ABCD中,AB
=
20cm,BC
=4cm,点P从A开始沿折线A-B-
C-D以4
cm/s的速度移动,点Q从C开始沿CD边以1cm/s的速度移动,如果点P,Q分别从A,C同时出发,其中一点到达D时,另一点也随之停止运动.设运动时间为t(s).
(1)t为何值时,四边形APQD为矩形?
(2)设四边形APQD的面积为S,求S与t的函数关系式,并写出自变量t的取值范围;
(3)如图
(b)
,如果?P和?Q的半径都是3
cm,那么l为何值时,
?P和?Q外切?
(直接写出答案,不必写过程)
6.如图.已知∠AOB=45°,
P是边OA上一点,OP=4,以点P为圆心画圆,?P交OA于点C(点P在O,
C之间).点Q是直线OB.上的一个动点,连PQ,交?P于点D,已知,当OQ=7时,=
(1)求OP半径的长;
(2)当点Q在射线OB上运动时,以点Q为圆心,OQ为半径作?Q,若?Q与?P相切,试求OQ的长度.
7.如图,已知点P在线段AB上,点O在线段AB延长线上。以点O为圆心,OP为半径作圆,点C是?O上的一点.
(1)如果AP=
2PB,
PB=
BO.求证:△CAO
△BCO;
(2)如果AP=
m(m是常数,且m>1),
BP=
1,
OP是OA,OB的比例中项.当点C在圆O上运动时,求AC
:
BC的值(结果用含m的式子表示);
(3)在(2)的条件下,讨论以BC为半径的?B和以CA为半径的?C的位置关系,并写出相应m的取值范围.
8.
已知:在Rt△ABC中,∠ACB
=
90°,
BC=6,
AC=
8,过点A作直线MN⊥AC.
(1)如图,点E是射线AM上的一个动点(不与点A重合),联结CE交AB于点P.若AE为x,
AP为y,求y关于x的函数解析式,并写出它的定义域;
(2)在射线AM上是否存在一点E,使以点E,
A,
P组成的三角形与△ABC相似,若存在求AE的长,若不存在,请说明理由;
(3)如图,过点B作BD⊥MN,垂足为D,以点C为圆心,若以AC为半径的?C与以ED为半径的?E相切,求?E的半径.
9.如图,已知sin∠ABC=,?O的半径为2,圆心O在射线BC上,?O与射线BA相交于E,
F两点,EF
=2.
(1)求BO的长;
(2)点P在射线BC上,以点P为圆心作圆,使得?P同时与?O和射线BA相切,求所有满足条件的?P的半径.
10.如图,在△ABC中,AB=AC=10,BC=12,点D在边BC上,且BD=4,以点D为顶点作∠EDF
=∠B,分别交边AB于点E,交射线CA于点F.
(1)当AE=6时,求AF的长:
(2)当以点C为圆心CF长为半径的?C和以点A为圆心AE长为半径的?A相切时,
求BE的长;
(3)当以边AC为直径的?O与线段DE相切时,求BE的长.
11.已知:如图.在等腰△ABC中,已知AB=
AC=3,
cos∠B=
,D为AB上一点过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.当BD长为何值时,以点F为圆心,线段FA为半径的圆与BC边相切?
.
12.如图,在?ABCD中,AB=2,∠A=
60°,以AB为直径的?O过点D,点M是
BC边上一点(点M不与B,
C重合),过点M作BC的垂线MN,交CD边于点N.
(1)求AD的长;
(2)以CN为直径作?P
,设BM
=
x,
?P的半径为y.
①求y关于x的函数关系式,并写出x的取值范围;
②当BM为何值时,?P与?O相切.
直线与圆、圆与圆的位置关系分类讨论
知识梳理,
直线与圆、圆与圆的位置关系是上海中考模拟卷及中考卷压轴题中的“常客”,由于牵涉到的条件较多,情况较为复杂,若没有掌握--定的解题规律和方法是很难快速求解的.直线与圆相切的充要条件是d=
r,其中d表示圆心到直线的距离,r表示圆的半径.而圆与圆相切含有两种情况,即圆与圆外切、圆与圆内切,它们的充要条件分别为d=
R+r和d
=|Rr|.其中d表示两圆的圆心距,R和r分别表示两圆的半径.此类问题的求解方法规律性甚强,第一步:列出二或三条件(d,
R,
r),第二步:根据题意列出方程并求解(d=r,
d=
R+r,
d
=|R-r|),第三步:检验解是否存在.掌握以上步骤不必画圆,按部就班便能顺利求解.
典型例题,
[例1]如图,已知:在△ABC中,
AB=AC=5,
BC=6,点D为BC边上一动点(不与B点重合),过点D作射线DE交AB边于点E,使∠BDE=∠A,以D为圆心,DC长为半径作?D.
(1)设BD=x,
AE=y,求y关于x的函数关系,并写出定义域;
(2)当?D与AB边相切时,求BD的长;
(3)如果?E是以E为圆心,
AE长为半径的圆,那么当BD为多少时,
?D与?E相切?
[思路分析]第(2)题是直线
与圆相切,根据题意列出D到AB的距离d,r=
CD为己知,若?D与AB边相切,则d=
r建立方程,求解检验便可.第(3)题根据题意列出D,
E两点的距离d,r=
CD,
R=
AE,若OD与OE相切,依据d=R+r或d
=|R-r|建立方程,求解检验便可.
[例2]如图,在△ABC中,∠BAC
=
90°,
AB
=
AC=
2,OA的半径为1.若点O在BC上运动(与点B,
C不重合),设BO=
x,△AOC的面积为y.
(1)求y关于x的函数解析式,并写出函数的定义域;
(2)以点O为圆心,BO长为半径作?O,求当?O与日?A相切时,△A
OC的面积.
[思路分析]本题只需讨论?O
与?A内切或者外切两种情况,两个圆的半径都方便表示,圆心距AO可看作直角三角形的斜边用勾股定理表示.
[例3]如图1,
?O的半径OA
=
1,点M是线段OA延长线上的任意一点,?M与?O
内切于点B,过点A作CD⊥OA交?M于点C,D,联结CM,OC,OC交?O于E,
设OM=x,△MOC的面积为y.
(1)求y关于x的函数解析式,并写出函数的定义域;
(2)将?O沿弦CD翻折得到ON,如图2.当OM=4时,试判断ON与直线CM的位置关系;
(3)将?O绕着点E旋转180°得到OP,如图3.如果?P与?M内切,求OM的长.
图1
图2
图3
练习题
1.如图,已知在直角梯形ABCD中,AB
//
CD,∠C=90°,CD=9,
BC=3,
tan∠A=。
P,
Q分别是边AB,CD上的动点(点P不与点A,点B重合),且有BP
=
2CQ.
(1)求AB的长;
(2)若以C为圆心、CQ为半径作?C,以P为圆心、以PA的长为半径作?P.当?C与?P外切时,试判断四边形PADQ是什么四边形,并说明理由.
2.在梯形ABCD中,∠ABC=90°,AD//BC,AB=8cm,BC=18cm,sin∠BCD=
,点P从点B开始沿BC边向终点C以每秒3
cm的速度移动,点Q从点D开始沿DA边向终点A以每秒2cm的速度移动,设运动时间为t(s).
(1)如图
(a)
,若四边形ABPQ是矩形,求t的值;
(2)若题设中的“BC=18cm”改变为“BC=kcm”,其他条件都不变,要使四边形PCDQ是等腰梯形,求t与k的函数关系式,并写出k的取值范围;
(3)如图
(b)
,如果?P的半径为6
cm,
?Q的半径为4
cm,在移动的过程中,试探索:t为何值时?P与?Q外离、外切、相交?
3.已知:如图,在Rt?ABC中,∠ACB
=
90°,
tan∠ABC
=,AB=5,
D是线段AB上的一点(与点A,
B不重合),直线DP⊥AB,与线段AC相交于点Q,与射线BC相交于点P,E是AQ的中点,线段ED的延长线与线段CB的延长线相交于点F.
(1)求证:△FBD
△FDP;
(2)求BF:
BP的值;
(3)若?A与直线BC相切,
?B的半径等于线段BF的长,设BD=x,当?A与?B相切时,请求出x的值.
4.如图,已知在矩形ABCD中,AB=3,
BC=4,
P是边BC延长线上的一点,联结AP交边CD于点E,把射线AP沿直线AD翻折,交射线CD于点Q,设CP=x,
DQ=y.
(1)求y关于x的函数解析式,并写出定义域.
(2)当以4为半径的OQ与直线AP相切,且?
A与?
Q也相切时,求?
A的半径.
5.如图(a)在矩形ABCD中,AB
=
20cm,BC
=4cm,点P从A开始沿折线A-B-
C-D以4
cm/s的速度移动,点Q从C开始沿CD边以1cm/s的速度移动,如果点P,Q分别从A,C同时出发,其中一点到达D时,另一点也随之停止运动.设运动时间为t(s).
(1)t为何值时,四边形APQD为矩形?
(2)设四边形APQD的面积为S,求S与t的函数关系式,并写出自变量t的取值范围;
(3)如图
(b)
,如果?P和?Q的半径都是3
cm,那么l为何值时,
?P和?Q外切?
(直接写出答案,不必写过程)
6.如图.已知∠AOB=45°,
P是边OA上一点,OP=4,以点P为圆心画圆,?P交OA于点C(点P在O,
C之间).点Q是直线OB.上的一个动点,连PQ,交?P于点D,已知,当OQ=7时,=
(1)求OP半径的长;
(2)当点Q在射线OB上运动时,以点Q为圆心,OQ为半径作?Q,若?Q与?P相切,试求OQ的长度.
7.如图,已知点P在线段AB上,点O在线段AB延长线上。以点O为圆心,OP为半径作圆,点C是?O上的一点.
(1)如果AP=
2PB,
PB=
BO.求证:△CAO
△BCO;
(2)如果AP=
m(m是常数,且m>1),
BP=
1,
OP是OA,OB的比例中项.当点C在圆O上运动时,求AC
:
BC的值(结果用含m的式子表示);
(3)在(2)的条件下,讨论以BC为半径的?B和以CA为半径的?C的位置关系,并写出相应m的取值范围.
8.
已知:在Rt△ABC中,∠ACB
=
90°,
BC=6,
AC=
8,过点A作直线MN⊥AC.
(1)如图,点E是射线AM上的一个动点(不与点A重合),联结CE交AB于点P.若AE为x,
AP为y,求y关于x的函数解析式,并写出它的定义域;
(2)在射线AM上是否存在一点E,使以点E,
A,
P组成的三角形与△ABC相似,若存在求AE的长,若不存在,请说明理由;
(3)如图,过点B作BD⊥MN,垂足为D,以点C为圆心,若以AC为半径的?C与以ED为半径的?E相切,求?E的半径.
9.如图,已知sin∠ABC=,?O的半径为2,圆心O在射线BC上,?O与射线BA相交于E,
F两点,EF
=2.
(1)求BO的长;
(2)点P在射线BC上,以点P为圆心作圆,使得?P同时与?O和射线BA相切,求所有满足条件的?P的半径.
10.如图,在△ABC中,AB=AC=10,BC=12,点D在边BC上,且BD=4,以点D为顶点作∠EDF
=∠B,分别交边AB于点E,交射线CA于点F.
(1)当AE=6时,求AF的长:
(2)当以点C为圆心CF长为半径的?C和以点A为圆心AE长为半径的?A相切时,
求BE的长;
(3)当以边AC为直径的?O与线段DE相切时,求BE的长.
11.已知:如图.在等腰△ABC中,已知AB=
AC=3,
cos∠B=
,D为AB上一点过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.当BD长为何值时,以点F为圆心,线段FA为半径的圆与BC边相切?
.
12.如图,在?ABCD中,AB=2,∠A=
60°,以AB为直径的?O过点D,点M是
BC边上一点(点M不与B,
C重合),过点M作BC的垂线MN,交CD边于点N.
(1)求AD的长;
(2)以CN为直径作?P
,设BM
=
x,
?P的半径为y.
①求y关于x的函数关系式,并写出x的取值范围;
②当BM为何值时,?P与?O相切.
