鲁教版 (五四制)八年级数学上册 第四章 图形的平移与旋转 章末测试题 (word版 含解析)
文档属性
| 名称 | 鲁教版 (五四制)八年级数学上册 第四章 图形的平移与旋转 章末测试题 (word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 188.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览


文档简介
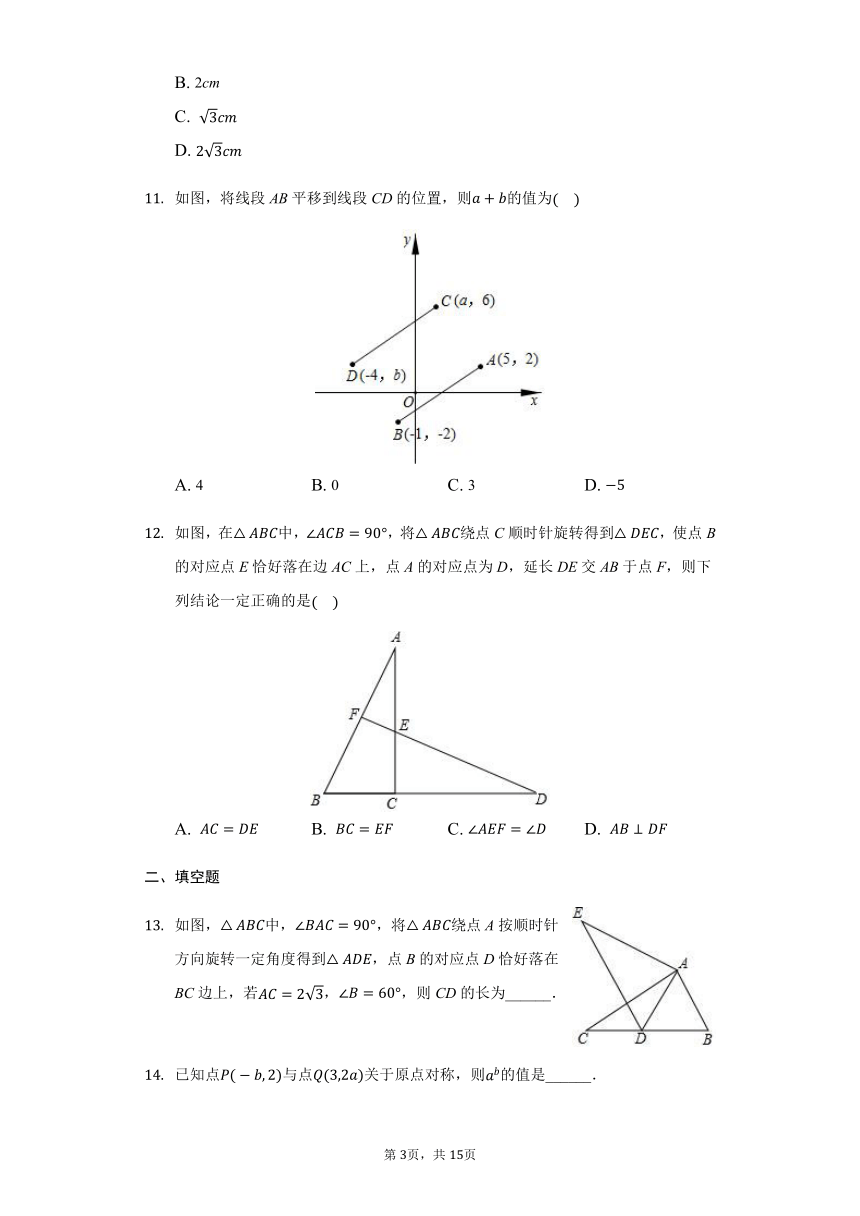
图形的平移与旋转章末测试题
一、选择题
如图所示的中心对称图形中,对称中心是
A.
B.
C.
D.
如图,在中,,,,将绕点A顺时针旋转度得到,当点B的对应点D恰好落在BC边上时,则CD的长为
A.
B.
C.
2
D.
下列图形是轴对称图形而不是中心对称图形的是
A.
B.
C.
D.
下列图案中,是轴对称图形,但不是中心对称图形的是
A.
B.
C.
D.
如图,在中,,,以C为旋转中心,将旋转到的位置,点B在斜边上,则为
A.
B.
C.
D.
平面直角坐标系内与点关于原点对称的点的坐标是
A.
B.
C.
D.
如图,在中,,将绕着点A顺时针旋转后,得到,且点在BC上,则的度数为
A.
B.
C.
D.
下列五种图形:平行四边形矩形菱形正方形,其中既是中心对称图形又是轴对称图形的共有
A.
1种
B.
2种
C.
3种
D.
4种
如图,在中,,,,把沿着直线BC的方向平移后得到,连接AE、AD,有以下结论;;;,其中正确的结论有
A.
1个
B.
2个
C.
3个
D.
4个
如图,在中,,,,将绕点A逆时针旋转得到,使点落在AB边上,连接,则的长度是
A.
1cm
B.
2cm
C.
D.
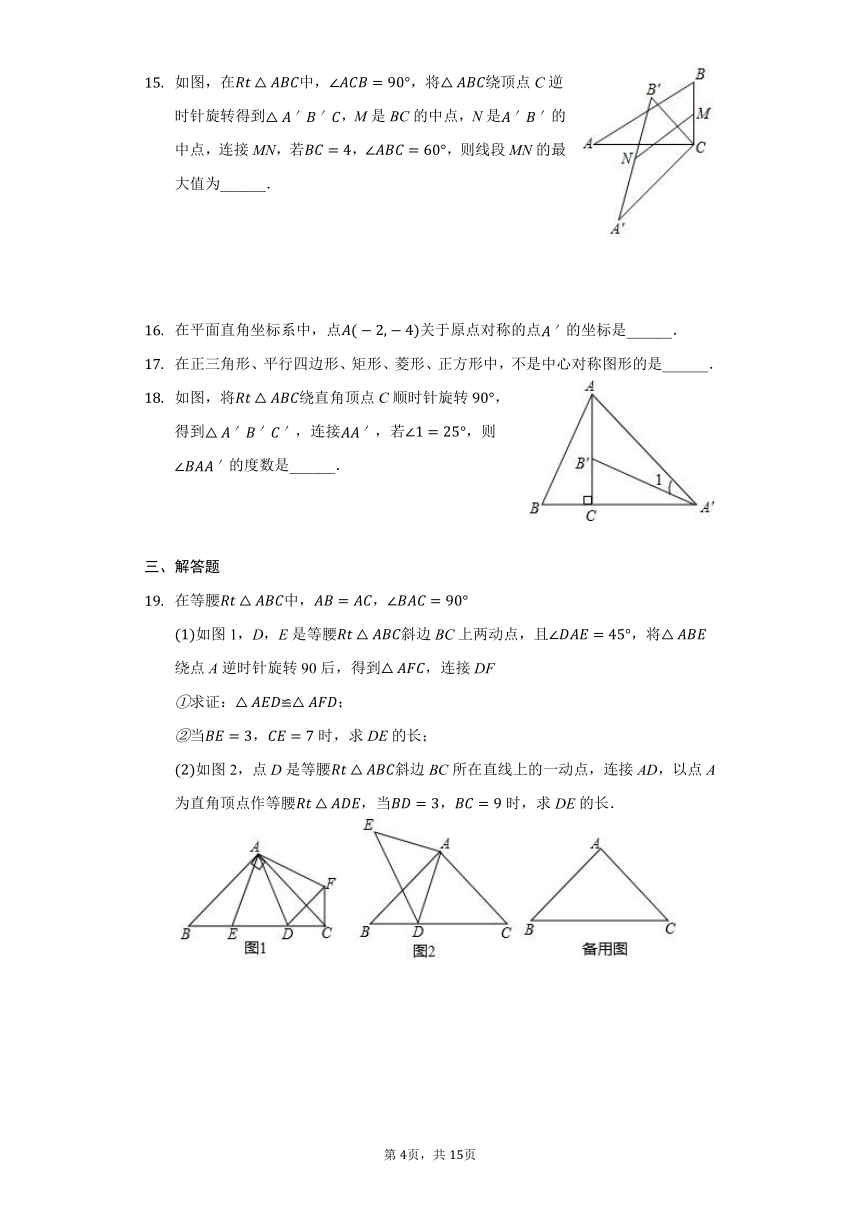
如图,将线段AB平移到线段CD的位置,则的值为
A.
4
B.
0
C.
3
D.
如图,在中,,将绕点C顺时针旋转得到,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是
A.
B.
C.
D.
二、填空题
如图,中,,将绕点A按顺时针方向旋转一定角度得到,点B的对应点D恰好落在BC边上,若,,则CD的长为______.
已知点与点关于原点对称,则的值是______.
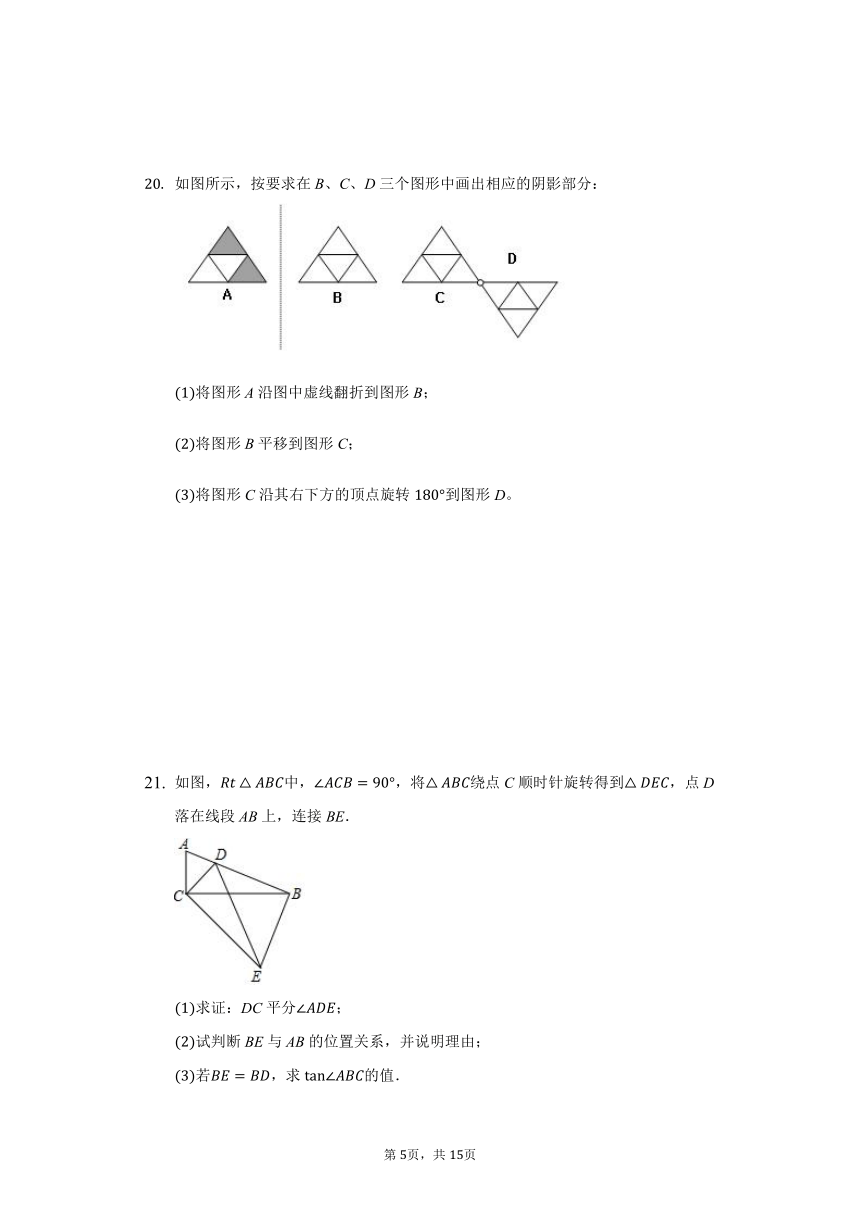
如图,在中,,将绕顶点C逆时针旋转得到,M是BC的中点,N是的中点,连接MN,若,,则线段MN的最大值为______.
在平面直角坐标系中,点关于原点对称的点的坐标是______.
在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是______.
如图,将绕直角顶点C顺时针旋转,得到,连接,若,则的度数是______.
三、解答题
在等腰中,,
如图1,D,E是等腰斜边BC上两动点,且,将绕点A逆时针旋转90后,得到,连接DF
求证:≌;
当,时,求DE的长;
如图2,点D是等腰斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰,当,时,求DE的长.
如图所示,按要求在B、C、D三个图形中画出相应的阴影部分:
将图形A沿图中虚线翻折到图形B;
将图形B平移到图形C;
将图形C沿其右下方的顶点旋转到图形D。
如图,中,,将绕点C顺时针旋转得到,点D落在线段AB上,连接BE.
求证:DC平分;
试判断BE与AB的位置关系,并说明理由;
若,求的值.
在中,,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转得到线段PQ。
若且点P与点M重合如图,线段CQ的延长线交射线BM于点D,请补全图形,并写出的度数为_______;直接填答案,不需写计算过程
在图2中,点P不与点重合,线段CQ的延长线与射线BM交于点D,猜想的大小用含的代数式表示,并加以证明.
答案和解析
1.【答案】B
【解析】解:如图所示的中心对称图形中,对称中心是.
2.【答案】A
【解析】解:由旋转的性质可知,,
,,
为等边三角形,
,
,
3.【答案】C
【解答】
解:A、既是轴对称图形又是中心对称图形,故本选项不符合题意;
B、既是轴对称图形又是中心对称图形,故本选项不符合题意;
C、是轴对称图形,不是中心对称图形,故本选项符合题意;
D、既是轴对称图形又是中心对称图形,故本选项不符合题意.
故选:C.
4.【答案】C
【解析】解:A、不是轴对称图形,是中心对称图形,故本选项不符合题意;
B、是轴对称图形,也是中心对称图形,故本选项不符合题意;
C、是轴对称图形,但不是中心对称图形,故本选项符合题意;
D、不是轴对称图形,也不是中心对称图形,故本选项不符合题意.
5.【答案】D
【解析】解:,,
,
以直角顶点C为旋转中心,将旋转到的位置,
,,
,
,
.
6.【答案】C
【解析】解:由题意,得
点关于原点对称的点的坐标是,
7.【答案】C
【解答】
解:将绕着点A顺时针旋转后,得到,,
,,,
,
,
,
,
,,
,
即的度数为,
故选C.
8.【答案】C
【解析】解:只是中心对称图形;、、两者都既是中心对称图形又是轴对称图形共3种.
9.【答案】D
【解析】解:沿着直线BC的方向平移后得到,
,故正确;
,故正确;
,故正确;
,
又,
,
,故正确;
10.【答案】B
【解析】解:在中,,,,
,则.
又由旋转的性质知,,,
是的中垂线,
.
根据旋转的性质知.
11.【答案】A
【解析】解:由题意,线段AB向左平移3个单位,再向上平移4个单位得到线段CD,
,,
,
12.【答案】D
【解答】
解:由旋转可得,≌,
,故A选项错误,
,故B选项错误,
,故C选项错误,
,
又,
,
,
,即,故D选项正确,
故选:D.
13.【答案】2
【解析】解:在中,,,
,,
由旋转得,,
,
,
,
14.【答案】
【解析】解:点与点关于原点对称,
,,
解得:,,
.
15.【答案】6
【解析】解:连接CN.
在中,,,
,
,
,
,
,
,
的最大值为6,
故答案为6.
连接根据直角三角形斜边中线的性质求出,利用三角形的三边关系即可解决问题.
16.【答案】
【解析】解:点关于原点对称的点的坐标是.
17.【答案】正三角形
【解析】解:在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是:正三角形.
18.【答案】
【解析】解:绕直角顶点C顺时针旋转得到,
,
是等腰直角三角形,
,
,
19.【答案】解:如图1中,
≌,
,,
,,
,
,,,
≌.
如图1中,设,则.
,,
,
,
,
≌,
,
在中,,,
,
,
.
当点E在线段BC上时,如图2中,连接BE.
,
,
,,
≌,
,,
,
,
.
当点D在CB的延长线上时,如图3中,连接BE.
同法可证是直角三角形,,,
,
综上所述,DE的值为或.
【解析】想办法证明,由,,即可证明.
如图1中,设,则在中,由,,推出,解方程即可.
分两种情形当点E在线段BC上时,如图2中,连接由≌,推出,,推出,推出,即可解决问题.
当点D在CB的延长线上时,如图3中,同法可得.
20.【答案】解:如图B所示:
如图C所示:
如图D所示:
21.【答案】证明:是由旋转得到,
,
,
,
平分.
解:结论:.
由旋转的性质可知,,
,C,E,B四点共圆,
,
,
,
.
如图,设BC交DE于连接AO.
,,
,
,E,B,D四点共圆,
,
,
,
,,
≌,
,
,
,
,
,
,
,
,设,则,
.
22.【答案】解:补全图形如图:
;
如图2,连接PC,AD,
,M是AC的中点,
,
即BD为AC的垂直平分线,
,,,
在与中,
≌,
,,
又,
,,,
,
,
,
,
.
第2页,共2页
第1页,共1页
一、选择题
如图所示的中心对称图形中,对称中心是
A.
B.
C.
D.
如图,在中,,,,将绕点A顺时针旋转度得到,当点B的对应点D恰好落在BC边上时,则CD的长为
A.
B.
C.
2
D.
下列图形是轴对称图形而不是中心对称图形的是
A.
B.
C.
D.
下列图案中,是轴对称图形,但不是中心对称图形的是
A.
B.
C.
D.
如图,在中,,,以C为旋转中心,将旋转到的位置,点B在斜边上,则为
A.
B.
C.
D.
平面直角坐标系内与点关于原点对称的点的坐标是
A.
B.
C.
D.
如图,在中,,将绕着点A顺时针旋转后,得到,且点在BC上,则的度数为
A.
B.
C.
D.
下列五种图形:平行四边形矩形菱形正方形,其中既是中心对称图形又是轴对称图形的共有
A.
1种
B.
2种
C.
3种
D.
4种
如图,在中,,,,把沿着直线BC的方向平移后得到,连接AE、AD,有以下结论;;;,其中正确的结论有
A.
1个
B.
2个
C.
3个
D.
4个
如图,在中,,,,将绕点A逆时针旋转得到,使点落在AB边上,连接,则的长度是
A.
1cm
B.
2cm
C.
D.
如图,将线段AB平移到线段CD的位置,则的值为
A.
4
B.
0
C.
3
D.
如图,在中,,将绕点C顺时针旋转得到,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是
A.
B.
C.
D.
二、填空题
如图,中,,将绕点A按顺时针方向旋转一定角度得到,点B的对应点D恰好落在BC边上,若,,则CD的长为______.
已知点与点关于原点对称,则的值是______.
如图,在中,,将绕顶点C逆时针旋转得到,M是BC的中点,N是的中点,连接MN,若,,则线段MN的最大值为______.
在平面直角坐标系中,点关于原点对称的点的坐标是______.
在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是______.
如图,将绕直角顶点C顺时针旋转,得到,连接,若,则的度数是______.
三、解答题
在等腰中,,
如图1,D,E是等腰斜边BC上两动点,且,将绕点A逆时针旋转90后,得到,连接DF
求证:≌;
当,时,求DE的长;
如图2,点D是等腰斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰,当,时,求DE的长.
如图所示,按要求在B、C、D三个图形中画出相应的阴影部分:
将图形A沿图中虚线翻折到图形B;
将图形B平移到图形C;
将图形C沿其右下方的顶点旋转到图形D。
如图,中,,将绕点C顺时针旋转得到,点D落在线段AB上,连接BE.
求证:DC平分;
试判断BE与AB的位置关系,并说明理由;
若,求的值.
在中,,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转得到线段PQ。
若且点P与点M重合如图,线段CQ的延长线交射线BM于点D,请补全图形,并写出的度数为_______;直接填答案,不需写计算过程
在图2中,点P不与点重合,线段CQ的延长线与射线BM交于点D,猜想的大小用含的代数式表示,并加以证明.
答案和解析
1.【答案】B
【解析】解:如图所示的中心对称图形中,对称中心是.
2.【答案】A
【解析】解:由旋转的性质可知,,
,,
为等边三角形,
,
,
3.【答案】C
【解答】
解:A、既是轴对称图形又是中心对称图形,故本选项不符合题意;
B、既是轴对称图形又是中心对称图形,故本选项不符合题意;
C、是轴对称图形,不是中心对称图形,故本选项符合题意;
D、既是轴对称图形又是中心对称图形,故本选项不符合题意.
故选:C.
4.【答案】C
【解析】解:A、不是轴对称图形,是中心对称图形,故本选项不符合题意;
B、是轴对称图形,也是中心对称图形,故本选项不符合题意;
C、是轴对称图形,但不是中心对称图形,故本选项符合题意;
D、不是轴对称图形,也不是中心对称图形,故本选项不符合题意.
5.【答案】D
【解析】解:,,
,
以直角顶点C为旋转中心,将旋转到的位置,
,,
,
,
.
6.【答案】C
【解析】解:由题意,得
点关于原点对称的点的坐标是,
7.【答案】C
【解答】
解:将绕着点A顺时针旋转后,得到,,
,,,
,
,
,
,
,,
,
即的度数为,
故选C.
8.【答案】C
【解析】解:只是中心对称图形;、、两者都既是中心对称图形又是轴对称图形共3种.
9.【答案】D
【解析】解:沿着直线BC的方向平移后得到,
,故正确;
,故正确;
,故正确;
,
又,
,
,故正确;
10.【答案】B
【解析】解:在中,,,,
,则.
又由旋转的性质知,,,
是的中垂线,
.
根据旋转的性质知.
11.【答案】A
【解析】解:由题意,线段AB向左平移3个单位,再向上平移4个单位得到线段CD,
,,
,
12.【答案】D
【解答】
解:由旋转可得,≌,
,故A选项错误,
,故B选项错误,
,故C选项错误,
,
又,
,
,
,即,故D选项正确,
故选:D.
13.【答案】2
【解析】解:在中,,,
,,
由旋转得,,
,
,
,
14.【答案】
【解析】解:点与点关于原点对称,
,,
解得:,,
.
15.【答案】6
【解析】解:连接CN.
在中,,,
,
,
,
,
,
,
的最大值为6,
故答案为6.
连接根据直角三角形斜边中线的性质求出,利用三角形的三边关系即可解决问题.
16.【答案】
【解析】解:点关于原点对称的点的坐标是.
17.【答案】正三角形
【解析】解:在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是:正三角形.
18.【答案】
【解析】解:绕直角顶点C顺时针旋转得到,
,
是等腰直角三角形,
,
,
19.【答案】解:如图1中,
≌,
,,
,,
,
,,,
≌.
如图1中,设,则.
,,
,
,
,
≌,
,
在中,,,
,
,
.
当点E在线段BC上时,如图2中,连接BE.
,
,
,,
≌,
,,
,
,
.
当点D在CB的延长线上时,如图3中,连接BE.
同法可证是直角三角形,,,
,
综上所述,DE的值为或.
【解析】想办法证明,由,,即可证明.
如图1中,设,则在中,由,,推出,解方程即可.
分两种情形当点E在线段BC上时,如图2中,连接由≌,推出,,推出,推出,即可解决问题.
当点D在CB的延长线上时,如图3中,同法可得.
20.【答案】解:如图B所示:
如图C所示:
如图D所示:
21.【答案】证明:是由旋转得到,
,
,
,
平分.
解:结论:.
由旋转的性质可知,,
,C,E,B四点共圆,
,
,
,
.
如图,设BC交DE于连接AO.
,,
,
,E,B,D四点共圆,
,
,
,
,,
≌,
,
,
,
,
,
,
,
,设,则,
.
22.【答案】解:补全图形如图:
;
如图2,连接PC,AD,
,M是AC的中点,
,
即BD为AC的垂直平分线,
,,,
在与中,
≌,
,,
又,
,,,
,
,
,
,
.
第2页,共2页
第1页,共1页
