人教版八年级数学上册第十二章12.3角平分线性质与判定综合练习(word版,解析版)
文档属性
| 名称 | 人教版八年级数学上册第十二章12.3角平分线性质与判定综合练习(word版,解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 21:49:20 | ||
图片预览




文档简介
角平分线性质与判定练习
一、选择题
1.
如图,OP平分∠AOB,PC⊥OA,PD⊥OB.垂足分别为C,D,则下列结论中错误的是??(????)
?
A.
PC=PD?????????????B.
OD=OC?????????????C.
∠DPO=∠CPO?????????????D.
PC=OC?????????????
2.
如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,则线段PN的最小值是??(????)
?
A.
2?????????????B.
3?????????????C.
4?????????????D.
5?????????????
3.
如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若,DE=2,AB=4,则AC=(????)
?
A.
4?????????????B.
3?????????????C.
6?????????????D.
5?????????????
4.
如图,AD是△ABC中的角平分线,于点E,,DE=2,AB=4,则AC长是(????)
?
A.
3?????????????B.
4?????????????C.
6?????????????D.
5?????????????
5.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6?cm,则△DEB的周长为??(????)
?
A.
4?cm?????????????B.
6?cm?????????????C.
10?cm?????????????D.
不能确定?????????????
6.
如图,△ABC中,?,点O为△ABC的三条角平分线的交点,,,,点D,E,F分别是垂足,且AB=10?cm,BC=8?cm,CA=6?cm,则点O到三边AB,AC和BC的距离分别为(????)
?
A.
2?cm,2?cm,2?cm?????????????B.
3?cm,3?cm,3?cm?????????????
?C.
4?cm,4?cm,4?cm?????????????D.
2?cm,3?cm,5?cm?????????????
7.
如图,OP平分,于点A,点Q是射线OM上一个动点,若PA=4,则PQ的最小值为(????)
?
A.
1?????????????B.
2?????????????C.
3?????????????D.
4?????????????
8.
如图,,,于D,,则的长度为(????)
?
A.
4?????????????B.
3?????????????C.
2?????????????D.
1?????????????
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是 ( )
?
A.
8?????????????B.
6?????????????C.
4?????????????D.
2?????????????
10.
如图,已知AB=AC,AE=AF,BE与CF交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上,以上结论中,正确的是??(????)
?
A.
①?????????????B.
②?????????????C.
①②?????????????D.
①②③?????????????
11.
如图所示,若AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于E,且PE=3?cm,则AB与CD之间的距离为??(????)
?
A.
3?cm?????????????B.
6?cm?????????????C.
9?cm?????????????D.
无法确定?????????????
12.
如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若BC=64,且BD:DC=9:7,则点D到AB边的距离为(????)
?
A.
18?????????????B.
32?????????????C.
28?????????????D.
24?????????????
13.
如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,则下面三个结论:①AS=AR,②QP∥AR,③△BRP≌△CSP,其中正确的是??(????)
?
A.
①③?????????????B.
②③?????????????C.
①②?????????????D.
①②③?????????????
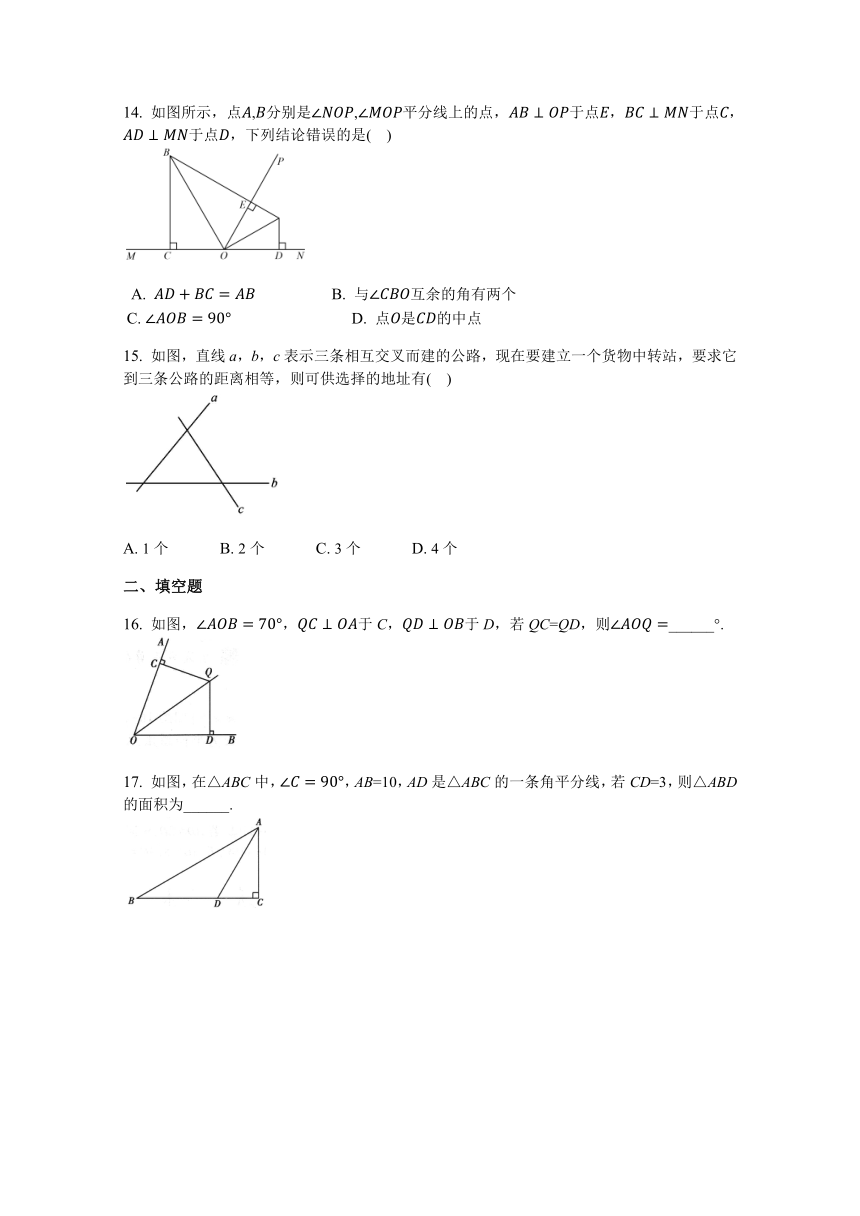
14.
如图所示,点,分别是,平分线上的点,于点,于点,于点,下列结论错误的是(????)
?
A.
?????????????
??
B.
与互余的角有两个?????????????
?C.
????????????
?D.
点是的中点?????????????
15.
如图,直线a,b,c表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(????)
?
A.
1个?????????????B.
2个?????????????C.
3个?????????????D.
4个?????????????
二、填空题
16.
如图,,于C,于D,若QC=QD,则______°.
?
17.
如图,在△ABC中,,AB=10,AD是△ABC的一条角平分线,若CD=3,则△ABD的面积为______.
?
18.
如图,,AD垂直平分线段BC于点D,的平分线BE交AD于点E,连接EC,则的度数是______.
?
19.
如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.下列结论:①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形,其中正确的有____.
?
20.
如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=30°,E为AC上一点,且AE=AD,则∠EDC的度数为____.
?
21.
如图所示,已知△ABC的周长是21,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是____.
?
22.
如图,在△ABC中,BC=5?cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是____cm.
?
23.
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则_______°.
?
24.
如图所示,在四边形中,,的平分线与的平分线交于点,则__________.
?
三、解答题
25.
证明:角的平分线上的点到角的两边的距离相等.
26.
如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
?求证:
?
(1)PE=PF;
(2)点P在∠BAC的平分线上.
27.
如图,在△ABC中,CA=CB,,AD平分,于点E,AB=10?cm.求△BED的周长.
?
28.
如图所示,,平分,.求的度数.
?
30.
如图所示,,分别是△ABC?的两条角平分线,且相交于点,求证点在的平分线上.
?
31.
如图,已知F,G是OA上两点,M,N是OB上两点,且FG=MN,△PFG和△PMN的面积相等.试判断点P是否在∠AOB的平分线上,并说明理由.
?
32.
已知:如图所示,,于,于点,交于点.求证:平分.
?
33.
如图,,分别是△ABC的外角和的平分线,它们交于点,于,于,求证:为的平分线.
?
34.
如图所示,在中,分别延长的边,到,,与的平分线相交点,爱动脑筋的小明在写作业时发现如下规律:
?
?①若,则;
?②若,则;
?③若,则.
(1)上述规律,若,则????????;
(2)请你用数学表达式归纳出与的关系;
(3)请说明第2题中结论的正确性.
35.
在△ABC中,AD是的平分线.
?
(1)如图①,求证:;
(2)如图②,若BD=CD,求证:AB=AC;
(3)如图③,若AB=5,AC=4,BC=6,求BD的长.
36.
工人师傅常用角尺平分一个任意角,做法如下:如图,是任意一个角,在边,上分别截取,移动角尺,使角尺两边相同的刻度分别与点,重合,过角尺顶点的射线便是的平分线.请结合图形说明理由.
?
37.
如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:
?(1)使其到两公路的距离相等;
?(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
?
四、证明题
38.
已知:如图,在中,,,是的平分线,求证:.
?
39.
如图,,M是BC的中点,DM平分,求证:AM平分.
?
40.
如图,,点是的中点,则平分,为什么?
?
41.
如图所示,射线OM,ON是两条公路,点A,B,C,D是四个小商店,其中A,B在公路OM上,C,D在公路ON上,且AB=CD,点P是一座购物商场,若,则商场P的位置恰好在的平分线上,为什么?
?
角平分线性质与判定练习
参考答案
一、选择题
1.
如图,OP平分∠AOB,PC⊥OA,PD⊥OB.垂足分别为C,D,则下列结论中错误的是??(????)
?
A.
PC=PD?????????????B.
OD=OC?????????????C.
∠DPO=∠CPO?????????????D.
PC=OC?????????????
【答案】D
【解析】根据角平分线的性质知PC=PD,由PD=PC,OP=OP知Rt△POD≌Rt△POC,所以∠DPO=∠CPO,OD=OC.
2.
如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,则线段PN的最小值是??(????)
?
A.
2?????????????B.
3?????????????C.
4?????????????D.
5?????????????
【答案】B
【解析】过点P作PQ⊥OB,垂足为Q,当N与Q重合时PN的值最小,由角平分线的性质知PQ=PM=3.故PN的最小值为3,故选B.
3.
如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若,DE=2,AB=4,则AC=(????)
?
A.
4?????????????B.
3?????????????C.
6?????????????D.
5?????????????
【答案】B
【解析】∵AD是△ABC中∠BAC的平分线,DE⊥AB,DF⊥AC,∴DF=DE=2.∵AB=4,∴.∵,∴,∴.故选B.
4.
如图,AD是△ABC中的角平分线,于点E,,DE=2,AB=4,则AC长是(????)
?
A.
3?????????????B.
4?????????????C.
6?????????????D.
5?????????????
【答案】A
【解析】如图,过点D作于F,∵AD是△ABC中的角平分线,
?,∴DE=DF,由图可知,.
?∴,解得AC=3.故选A.
?
5.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6?cm,则△DEB的周长为??(????)
?
A.
4?cm?????????????B.
6?cm?????????????C.
10?cm?????????????D.
不能确定?????????????
【答案】B
【解析】由题意知∠C=∠AED=90°,又因为AD平分∠CAB,所以DE=DC.易证△ADE≌△ADC,
?所以AE=AC.△DEB的周长=BD+DE+BE=BD+DC+BE=BC+BE=AC+BE=AE+BE=AB=6?cm,故选B.
6.
如图,△ABC中,?,点O为△ABC的三条角平分线的交点,,,,点D,E,F分别是垂足,且AB=10?cm,BC=8?cm,CA=6?cm,则点O到三边AB,AC和BC的距离分别为(????)
?
A.
2?cm,2?cm,2?cm?????????????B.
3?cm,3?cm,3?cm?????????????
?C.
4?cm,4?cm,4?cm?????????????D.
2?cm,3?cm,5?cm?????????????
【答案】A
【解析】点O为△ABC的三条角平分线的交点,,,,所以OF=OD=OE,根据,得AB·OF+BC·OD+AC·OE=48,所以OF=?OD=OF=2?cm.
7.
如图,OP平分,于点A,点Q是射线OM上一个动点,若PA=4,则PQ的最小值为(????)
?
A.
1?????????????B.
2?????????????C.
3?????????????D.
4?????????????
【答案】D
【解析】根据垂线段最短,得当时,PQ的值最小.又OP是的平分线,,所以PA=PQ=4.故选D.
8.
如图,,,于D,,则的长度为(????)
?
A.
4?????????????B.
3?????????????C.
2?????????????D.
1?????????????
【答案】D
【解析】作于,根据角平分线的性质可行,根据平行线的性质可得,由直角三角形角所对的直角边等于斜边的一半,可求得,即可求得,故选D.
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是 ( )
?
A.
8?????????????B.
6?????????????C.
4?????????????D.
2?????????????
【答案】C
【解析】本题考查角平分线的性质.
?过点P作PE⊥BC于E,?则点P到BC的距离是PE.
?
?∵AB∥CD,PA⊥AB,∴PD⊥CD.
?∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE,∴PE=PA=PD.
?∵PA+PD=AD=8,∴PA=PD=4,∴PE=4.故选C.
10.
如图,已知AB=AC,AE=AF,BE与CF交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上,以上结论中,正确的是??(????)
?
A.
①?????????????B.
②?????????????C.
①②?????????????D.
①②③?????????????
【答案】D
【解析】根据三角形全等的判定方法,由SAS可判定△ABE≌△ACF;由AAS可判定△BDF≌△CDE;连接AD,由SAS可判定△ACD≌△ABD,所以∠CAD=∠BAD,D在∠BAC的平分线上.故①②③均正确.
11.
如图所示,若AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于E,且PE=3?cm,则AB与CD之间的距离为??(????)
?
A.
3?cm?????????????B.
6?cm?????????????C.
9?cm?????????????D.
无法确定?????????????
【答案】B
【解析】如图,过点P作PM⊥AB于M,并反向延长交CD于点N,则PN⊥CD,且MN的长为AB与CD之间的距离.由角平分线的性质得PM=PE,PN=PE,∴MN=PM+PN=2PE=6?cm.
?
12.
如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若BC=64,且BD:DC=9:7,则点D到AB边的距离为(????)
?
A.
18?????????????B.
32?????????????C.
28?????????????D.
24?????????????
【答案】C
【解析】由BC=64,且BD:DC=9:7,可求得DC=28.
?过点D作DE⊥AB,垂足为E,因为AD平分∠BAC,DE⊥AB,DC⊥AC,所以DE=DC=28,故选C.
13.
如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,则下面三个结论:①AS=AR,②QP∥AR,③△BRP≌△CSP,其中正确的是??(????)
?
A.
①③?????????????B.
②③?????????????C.
①②?????????????D.
①②③?????????????
【答案】C
【解析】连接AP,由PR⊥AB于R,PS⊥AC于S,PR=PS,知AP平分∠BAC,所以∠RAP=∠QAP.因为AQ=PQ,所以∠QAP=∠QPA,所以∠RAP=∠QPA,所以QP∥AR.易证Rt△APR≌Rt△APS.所以AR=AS.由已知条件不能得到△BRP≌△CSP,故选C.
14.
如图所示,点,分别是,平分线上的点,于点,于点,于点,下列结论错误的是(????)
?
A.
?????????????
??
B.
与互余的角有两个?????????????
?C.
????????????
?D.
点是的中点?????????????
【答案】B
【解析】∵平分,∴,又,,∴△BCO≌△BEO?,同理,△AOD≌△AOE?,∴,,∴.故A正确.
?∵,,∴,即,故C正确.∵△BCO≌△BEO?,△AOD≌△AOE?,∴,,∴,即点是的中点.故D正确.
15.
如图,直线a,b,c表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(????)
?
A.
1个?????????????B.
2个?????????????C.
3个?????????????D.
4个?????????????
【答案】D
【解析】∵三角形内角平分线的变点到三角形三边的距离相等,∴三角形内角平分线的交点满足条件;如图:点P是△ABC两条外角平分线的交点,过点P作,,,∴PE=PF,PF=PD,∴PE=PF=PD,∴点P到△ABC的三边的距离相等,∴△ABC两条外角平分线的交点到其三边的距离也相等,满足此条件的点有3个,综上,到三条公路的距离相等的点有4个,∴可供选择的地址有4个.故选D.
?
二、填空题
16.
如图,,于C,于D,若QC=QD,则______°.
?
【答案】35
【解析】∵,,QC=QD,∴点Q在的平分线上,∴,∵,∴.
17.
如图,在△ABC中,,AB=10,AD是△ABC的一条角平分线,若CD=3,则△ABD的面积为______.
?
【答案】15
【解析】作于E.∵AD平分,,,∴DE=CD=3.
?∴△ABD的面积为.故答案是15.
?
18.
如图,,AD垂直平分线段BC于点D,的平分线BE交AD于点E,连接EC,则的度数是______.
?
【答案】115°
【解析】因为BE是的平分线,,所以.因为AD是BC的垂直平分线,所以,,
?所以.
19.
如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.下列结论:①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形,其中正确的有____.
?
【答案】①②③④
【解析】在△ABC中,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,AD为公共边,∴△ADE≌△ADF,∴∠EDA=∠FDA,AE=AF,DE=DF,故①②正确.∵AB=AC,AD是∠BAC的平分线,∴AD垂直平分BC,∴AD上的点到B,C两点的距离相等,③正确.根据图形的对称性可知,图中共有3对全等三角形,④正确.故填①②③④.
20.
如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=30°,E为AC上一点,且AE=AD,则∠EDC的度数为____.
?
【答案】15°
【解析】在△ABC中,D为BC的中点,AB=AC,∴AD为∠BAC的平分线,AD⊥BC.∵∠BAD=30°,∴∠DAE=30°,
?又∵AD=AE,∴∠ADE=75°,
?∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
21.
如图所示,已知△ABC的周长是21,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是____.
?
【答案】31.5
【解析】作OE⊥AC,OF⊥AB,垂足分别为E,F,连接OA,
?∵BO和CO分别平分∠ABC和∠ACB,OD⊥BC,
?∴OD=OE=OF.
?
22.
如图,在△ABC中,BC=5?cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是____cm.
?
【答案】5
【解析】∵BP平分∠ABC,∴∠ABP=∠DBP,
?∵AB∥PD,∴∠ABP=∠BPD,∴∠DBP=∠BPD,∴PD=BD,同理可得PE=EC,∴△PDE的周长=PD+PE+DE=BD+EC+DE=BC=5?cm.
23.
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则_______°.
?
【答案】35
【解析】∵QC⊥OA,QD⊥OB,QC=QD,∴点Q在∠AOB的平分线上,∴,∵∠AOB=70°,∴35°.
24.
如图所示,在四边形中,,的平分线与的平分线交于点,则__________.
?
【答案】
【解析】∵的平分线与的平分线交于点,∴,,
?又∵,∴.∵在四边形中,,∴.
?∴.
三、解答题
25.
证明:角的平分线上的点到角的两边的距离相等.
【答案】解:如图,,点在上,,垂足分别为,,求证.
?证明:∵,,∴.
?在△PDO?和△PEO中,∴△PDO≌△PEO?(AAS).∴,即角的平分线上的点到角的两边的距离相等.
?
26.
如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
?求证:
?
(1)PE=PF;
【答案】连接AP,∵PE⊥AB,PF⊥AC,
?∴∠AEP=∠AFP=90°.?∵AE=AF,AP=AP,
?∴Rt△AEP≌Rt△AFP(HL),∴PE=PF.
(2)点P在∠BAC的平分线上.
【答案】由第1问知Rt△AEP≌Rt△AFP,
?∴∠EAP=∠FAP,
?∴点P在∠BAC的平分线上.
27.
如图,在△ABC中,CA=CB,,AD平分,于点E,AB=10?cm.求△BED的周长.
?
【答案】∵,,
?∴CD=DE.又∵AD=AD,∴,∴,AC=AE,∴BD+DE=BD+DC=BC.
?∵AC=CB,∴BD+DE=BC=CA=AE,∴BD+DE+BE=AE+BE=AB=10?cm,∴△BED的周长为10?cm.
28.
如图所示,,平分,.求的度数.
?
【答案】50°
【解析】∵,∴.∵平分,∴,∵,∴.
29.
如图,在△ABC中,,,CE平分,于D,于F,求的度数.?
?
【答案】∵,,,∴.
?∵CE平分,∴.
?又∵,∴,
?∴,
?∵,∴.
30.
如图所示,,分别是△ABC?的两条角平分线,且相交于点,求证点在的平分线上.
?
【答案】证明:如图,过点作,,分别垂直于,,,垂足分别为,,.∴.同理,?.∴.∴点在的平分线上.
?
31.
如图,已知F,G是OA上两点,M,N是OB上两点,且FG=MN,△PFG和△PMN的面积相等.试判断点P是否在∠AOB的平分线上,并说明理由.
?
【答案】点P在∠AOB的平分线上.
?理由:如图所示,作PD⊥OA于D,PE⊥OB于E.
?
?∵,,
?,
?∴=.
?又∵FG=MN,∴PD=PE,∴点P在∠AOB的平分线上.
32.
已知:如图所示,,于,于点,交于点.求证:平分.
?
【答案】证明:∵,,∴.
?在△BDE?和△CDF中,∴△BDE≌△CDF(AAS),∴,
?又∵,,∴平分.
33.
如图,,分别是△ABC的外角和的平分线,它们交于点,于,于,求证:为的平分线.
?
【答案】证明:如图,过点作于.∵,,,分别是和的平分线,∴,,∴.
?又∵,,∴点在的平分线上,∴为的平分线.
34.
如图所示,在中,分别延长的边,到,,与的平分线相交点,爱动脑筋的小明在写作业时发现如下规律:
?
?①若,则;
?②若,则;
?③若,则.
(1)上述规律,若,则????????;
【答案】15°
(2)请你用数学表达式归纳出与的关系;
【答案】.
(3)请说明第2题中结论的正确性.
【答案】证明:因为是的一个外角,
?所以.
?因为是的平分线,
?所以.
?同理,可得.
?因为,
?所以
?
?
?.
35.
在△ABC中,AD是的平分线.
?
(1)如图①,求证:;
【答案】证明:如图,作于E,于F.
?
?∵AD是的平分线,∴DE=DF.
?∴.
(2)如图②,若BD=CD,求证:AB=AC;
【答案】证明:∵BD=CD,∴.
?由第1问知,
?∴,∴AB=AC.
(3)如图③,若AB=5,AC=4,BC=6,求BD的长.
【答案】如图,过A作,垂足为M.
?∵,,∴,
?由第1问知,∴.又BC=6,∴.
?
36.
工人师傅常用角尺平分一个任意角,做法如下:如图,是任意一个角,在边,上分别截取,移动角尺,使角尺两边相同的刻度分别与点,重合,过角尺顶点的射线便是的平分线.请结合图形说明理由.
?
【答案】在和中,,,,∴,∴,即平分.
37.
如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:
?(1)使其到两公路的距离相等;
?(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
?
【答案】解:如图,连接,作的平分线交于点,则点就是所要建超市的位置.
?
四、证明题
38.
已知:如图,在中,,,是的平分线,求证:.
?
【答案】证明?:∵,
?∴,
?∵,
?∴,
?∴,,
?∵是的平分线,
?∴,
?∴,∴,
?在中,∵,
?∴,
?.
39.
如图,,M是BC的中点,DM平分,求证:AM平分.
?
【答案】过点M作于N.
?∵DM平分,?,
?∴CM=MM.又M是BC的中点,
?∴CM=BM,∴MN=MB.
?又∵,∴,∴AM平分.
40.
如图,,点是的中点,则平分,为什么?
?
【答案】如图,
?
?连接.点是的中点,∴.
?在和中,∵,
?∴.
?在和中,∴,
?∴,∴,∴平分.
41.
如图所示,射线OM,ON是两条公路,点A,B,C,D是四个小商店,其中A,B在公路OM上,C,D在公路ON上,且AB=CD,点P是一座购物商场,若,则商场P的位置恰好在的平分线上,为什么?
?
【答案】过点P作于点E,于点F,如图所示.
?
?∵,,,
?∴AB·PE=CD·PF.∵AB=CD,∴PE=PF.∴点P在的平分线上.
一、选择题
1.
如图,OP平分∠AOB,PC⊥OA,PD⊥OB.垂足分别为C,D,则下列结论中错误的是??(????)
?
A.
PC=PD?????????????B.
OD=OC?????????????C.
∠DPO=∠CPO?????????????D.
PC=OC?????????????
2.
如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,则线段PN的最小值是??(????)
?
A.
2?????????????B.
3?????????????C.
4?????????????D.
5?????????????
3.
如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若,DE=2,AB=4,则AC=(????)
?
A.
4?????????????B.
3?????????????C.
6?????????????D.
5?????????????
4.
如图,AD是△ABC中的角平分线,于点E,,DE=2,AB=4,则AC长是(????)
?
A.
3?????????????B.
4?????????????C.
6?????????????D.
5?????????????
5.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6?cm,则△DEB的周长为??(????)
?
A.
4?cm?????????????B.
6?cm?????????????C.
10?cm?????????????D.
不能确定?????????????
6.
如图,△ABC中,?,点O为△ABC的三条角平分线的交点,,,,点D,E,F分别是垂足,且AB=10?cm,BC=8?cm,CA=6?cm,则点O到三边AB,AC和BC的距离分别为(????)
?
A.
2?cm,2?cm,2?cm?????????????B.
3?cm,3?cm,3?cm?????????????
?C.
4?cm,4?cm,4?cm?????????????D.
2?cm,3?cm,5?cm?????????????
7.
如图,OP平分,于点A,点Q是射线OM上一个动点,若PA=4,则PQ的最小值为(????)
?
A.
1?????????????B.
2?????????????C.
3?????????????D.
4?????????????
8.
如图,,,于D,,则的长度为(????)
?
A.
4?????????????B.
3?????????????C.
2?????????????D.
1?????????????
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是 ( )
?
A.
8?????????????B.
6?????????????C.
4?????????????D.
2?????????????
10.
如图,已知AB=AC,AE=AF,BE与CF交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上,以上结论中,正确的是??(????)
?
A.
①?????????????B.
②?????????????C.
①②?????????????D.
①②③?????????????
11.
如图所示,若AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于E,且PE=3?cm,则AB与CD之间的距离为??(????)
?
A.
3?cm?????????????B.
6?cm?????????????C.
9?cm?????????????D.
无法确定?????????????
12.
如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若BC=64,且BD:DC=9:7,则点D到AB边的距离为(????)
?
A.
18?????????????B.
32?????????????C.
28?????????????D.
24?????????????
13.
如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,则下面三个结论:①AS=AR,②QP∥AR,③△BRP≌△CSP,其中正确的是??(????)
?
A.
①③?????????????B.
②③?????????????C.
①②?????????????D.
①②③?????????????
14.
如图所示,点,分别是,平分线上的点,于点,于点,于点,下列结论错误的是(????)
?
A.
?????????????
??
B.
与互余的角有两个?????????????
?C.
????????????
?D.
点是的中点?????????????
15.
如图,直线a,b,c表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(????)
?
A.
1个?????????????B.
2个?????????????C.
3个?????????????D.
4个?????????????
二、填空题
16.
如图,,于C,于D,若QC=QD,则______°.
?
17.
如图,在△ABC中,,AB=10,AD是△ABC的一条角平分线,若CD=3,则△ABD的面积为______.
?
18.
如图,,AD垂直平分线段BC于点D,的平分线BE交AD于点E,连接EC,则的度数是______.
?
19.
如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.下列结论:①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形,其中正确的有____.
?
20.
如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=30°,E为AC上一点,且AE=AD,则∠EDC的度数为____.
?
21.
如图所示,已知△ABC的周长是21,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是____.
?
22.
如图,在△ABC中,BC=5?cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是____cm.
?
23.
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则_______°.
?
24.
如图所示,在四边形中,,的平分线与的平分线交于点,则__________.
?
三、解答题
25.
证明:角的平分线上的点到角的两边的距离相等.
26.
如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
?求证:
?
(1)PE=PF;
(2)点P在∠BAC的平分线上.
27.
如图,在△ABC中,CA=CB,,AD平分,于点E,AB=10?cm.求△BED的周长.
?
28.
如图所示,,平分,.求的度数.
?
30.
如图所示,,分别是△ABC?的两条角平分线,且相交于点,求证点在的平分线上.
?
31.
如图,已知F,G是OA上两点,M,N是OB上两点,且FG=MN,△PFG和△PMN的面积相等.试判断点P是否在∠AOB的平分线上,并说明理由.
?
32.
已知:如图所示,,于,于点,交于点.求证:平分.
?
33.
如图,,分别是△ABC的外角和的平分线,它们交于点,于,于,求证:为的平分线.
?
34.
如图所示,在中,分别延长的边,到,,与的平分线相交点,爱动脑筋的小明在写作业时发现如下规律:
?
?①若,则;
?②若,则;
?③若,则.
(1)上述规律,若,则????????;
(2)请你用数学表达式归纳出与的关系;
(3)请说明第2题中结论的正确性.
35.
在△ABC中,AD是的平分线.
?
(1)如图①,求证:;
(2)如图②,若BD=CD,求证:AB=AC;
(3)如图③,若AB=5,AC=4,BC=6,求BD的长.
36.
工人师傅常用角尺平分一个任意角,做法如下:如图,是任意一个角,在边,上分别截取,移动角尺,使角尺两边相同的刻度分别与点,重合,过角尺顶点的射线便是的平分线.请结合图形说明理由.
?
37.
如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:
?(1)使其到两公路的距离相等;
?(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
?
四、证明题
38.
已知:如图,在中,,,是的平分线,求证:.
?
39.
如图,,M是BC的中点,DM平分,求证:AM平分.
?
40.
如图,,点是的中点,则平分,为什么?
?
41.
如图所示,射线OM,ON是两条公路,点A,B,C,D是四个小商店,其中A,B在公路OM上,C,D在公路ON上,且AB=CD,点P是一座购物商场,若,则商场P的位置恰好在的平分线上,为什么?
?
角平分线性质与判定练习
参考答案
一、选择题
1.
如图,OP平分∠AOB,PC⊥OA,PD⊥OB.垂足分别为C,D,则下列结论中错误的是??(????)
?
A.
PC=PD?????????????B.
OD=OC?????????????C.
∠DPO=∠CPO?????????????D.
PC=OC?????????????
【答案】D
【解析】根据角平分线的性质知PC=PD,由PD=PC,OP=OP知Rt△POD≌Rt△POC,所以∠DPO=∠CPO,OD=OC.
2.
如图,若OP平分∠AOB,PM⊥OA于M点,PM=3,N是OB上一个动点,则线段PN的最小值是??(????)
?
A.
2?????????????B.
3?????????????C.
4?????????????D.
5?????????????
【答案】B
【解析】过点P作PQ⊥OB,垂足为Q,当N与Q重合时PN的值最小,由角平分线的性质知PQ=PM=3.故PN的最小值为3,故选B.
3.
如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.若,DE=2,AB=4,则AC=(????)
?
A.
4?????????????B.
3?????????????C.
6?????????????D.
5?????????????
【答案】B
【解析】∵AD是△ABC中∠BAC的平分线,DE⊥AB,DF⊥AC,∴DF=DE=2.∵AB=4,∴.∵,∴,∴.故选B.
4.
如图,AD是△ABC中的角平分线,于点E,,DE=2,AB=4,则AC长是(????)
?
A.
3?????????????B.
4?????????????C.
6?????????????D.
5?????????????
【答案】A
【解析】如图,过点D作于F,∵AD是△ABC中的角平分线,
?,∴DE=DF,由图可知,.
?∴,解得AC=3.故选A.
?
5.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6?cm,则△DEB的周长为??(????)
?
A.
4?cm?????????????B.
6?cm?????????????C.
10?cm?????????????D.
不能确定?????????????
【答案】B
【解析】由题意知∠C=∠AED=90°,又因为AD平分∠CAB,所以DE=DC.易证△ADE≌△ADC,
?所以AE=AC.△DEB的周长=BD+DE+BE=BD+DC+BE=BC+BE=AC+BE=AE+BE=AB=6?cm,故选B.
6.
如图,△ABC中,?,点O为△ABC的三条角平分线的交点,,,,点D,E,F分别是垂足,且AB=10?cm,BC=8?cm,CA=6?cm,则点O到三边AB,AC和BC的距离分别为(????)
?
A.
2?cm,2?cm,2?cm?????????????B.
3?cm,3?cm,3?cm?????????????
?C.
4?cm,4?cm,4?cm?????????????D.
2?cm,3?cm,5?cm?????????????
【答案】A
【解析】点O为△ABC的三条角平分线的交点,,,,所以OF=OD=OE,根据,得AB·OF+BC·OD+AC·OE=48,所以OF=?OD=OF=2?cm.
7.
如图,OP平分,于点A,点Q是射线OM上一个动点,若PA=4,则PQ的最小值为(????)
?
A.
1?????????????B.
2?????????????C.
3?????????????D.
4?????????????
【答案】D
【解析】根据垂线段最短,得当时,PQ的值最小.又OP是的平分线,,所以PA=PQ=4.故选D.
8.
如图,,,于D,,则的长度为(????)
?
A.
4?????????????B.
3?????????????C.
2?????????????D.
1?????????????
【答案】D
【解析】作于,根据角平分线的性质可行,根据平行线的性质可得,由直角三角形角所对的直角边等于斜边的一半,可求得,即可求得,故选D.
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是 ( )
?
A.
8?????????????B.
6?????????????C.
4?????????????D.
2?????????????
【答案】C
【解析】本题考查角平分线的性质.
?过点P作PE⊥BC于E,?则点P到BC的距离是PE.
?
?∵AB∥CD,PA⊥AB,∴PD⊥CD.
?∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE,∴PE=PA=PD.
?∵PA+PD=AD=8,∴PA=PD=4,∴PE=4.故选C.
10.
如图,已知AB=AC,AE=AF,BE与CF交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上,以上结论中,正确的是??(????)
?
A.
①?????????????B.
②?????????????C.
①②?????????????D.
①②③?????????????
【答案】D
【解析】根据三角形全等的判定方法,由SAS可判定△ABE≌△ACF;由AAS可判定△BDF≌△CDE;连接AD,由SAS可判定△ACD≌△ABD,所以∠CAD=∠BAD,D在∠BAC的平分线上.故①②③均正确.
11.
如图所示,若AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于E,且PE=3?cm,则AB与CD之间的距离为??(????)
?
A.
3?cm?????????????B.
6?cm?????????????C.
9?cm?????????????D.
无法确定?????????????
【答案】B
【解析】如图,过点P作PM⊥AB于M,并反向延长交CD于点N,则PN⊥CD,且MN的长为AB与CD之间的距离.由角平分线的性质得PM=PE,PN=PE,∴MN=PM+PN=2PE=6?cm.
?
12.
如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若BC=64,且BD:DC=9:7,则点D到AB边的距离为(????)
?
A.
18?????????????B.
32?????????????C.
28?????????????D.
24?????????????
【答案】C
【解析】由BC=64,且BD:DC=9:7,可求得DC=28.
?过点D作DE⊥AB,垂足为E,因为AD平分∠BAC,DE⊥AB,DC⊥AC,所以DE=DC=28,故选C.
13.
如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,则下面三个结论:①AS=AR,②QP∥AR,③△BRP≌△CSP,其中正确的是??(????)
?
A.
①③?????????????B.
②③?????????????C.
①②?????????????D.
①②③?????????????
【答案】C
【解析】连接AP,由PR⊥AB于R,PS⊥AC于S,PR=PS,知AP平分∠BAC,所以∠RAP=∠QAP.因为AQ=PQ,所以∠QAP=∠QPA,所以∠RAP=∠QPA,所以QP∥AR.易证Rt△APR≌Rt△APS.所以AR=AS.由已知条件不能得到△BRP≌△CSP,故选C.
14.
如图所示,点,分别是,平分线上的点,于点,于点,于点,下列结论错误的是(????)
?
A.
?????????????
??
B.
与互余的角有两个?????????????
?C.
????????????
?D.
点是的中点?????????????
【答案】B
【解析】∵平分,∴,又,,∴△BCO≌△BEO?,同理,△AOD≌△AOE?,∴,,∴.故A正确.
?∵,,∴,即,故C正确.∵△BCO≌△BEO?,△AOD≌△AOE?,∴,,∴,即点是的中点.故D正确.
15.
如图,直线a,b,c表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(????)
?
A.
1个?????????????B.
2个?????????????C.
3个?????????????D.
4个?????????????
【答案】D
【解析】∵三角形内角平分线的变点到三角形三边的距离相等,∴三角形内角平分线的交点满足条件;如图:点P是△ABC两条外角平分线的交点,过点P作,,,∴PE=PF,PF=PD,∴PE=PF=PD,∴点P到△ABC的三边的距离相等,∴△ABC两条外角平分线的交点到其三边的距离也相等,满足此条件的点有3个,综上,到三条公路的距离相等的点有4个,∴可供选择的地址有4个.故选D.
?
二、填空题
16.
如图,,于C,于D,若QC=QD,则______°.
?
【答案】35
【解析】∵,,QC=QD,∴点Q在的平分线上,∴,∵,∴.
17.
如图,在△ABC中,,AB=10,AD是△ABC的一条角平分线,若CD=3,则△ABD的面积为______.
?
【答案】15
【解析】作于E.∵AD平分,,,∴DE=CD=3.
?∴△ABD的面积为.故答案是15.
?
18.
如图,,AD垂直平分线段BC于点D,的平分线BE交AD于点E,连接EC,则的度数是______.
?
【答案】115°
【解析】因为BE是的平分线,,所以.因为AD是BC的垂直平分线,所以,,
?所以.
19.
如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.下列结论:①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形,其中正确的有____.
?
【答案】①②③④
【解析】在△ABC中,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,AD为公共边,∴△ADE≌△ADF,∴∠EDA=∠FDA,AE=AF,DE=DF,故①②正确.∵AB=AC,AD是∠BAC的平分线,∴AD垂直平分BC,∴AD上的点到B,C两点的距离相等,③正确.根据图形的对称性可知,图中共有3对全等三角形,④正确.故填①②③④.
20.
如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=30°,E为AC上一点,且AE=AD,则∠EDC的度数为____.
?
【答案】15°
【解析】在△ABC中,D为BC的中点,AB=AC,∴AD为∠BAC的平分线,AD⊥BC.∵∠BAD=30°,∴∠DAE=30°,
?又∵AD=AE,∴∠ADE=75°,
?∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
21.
如图所示,已知△ABC的周长是21,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是____.
?
【答案】31.5
【解析】作OE⊥AC,OF⊥AB,垂足分别为E,F,连接OA,
?∵BO和CO分别平分∠ABC和∠ACB,OD⊥BC,
?∴OD=OE=OF.
?
22.
如图,在△ABC中,BC=5?cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是____cm.
?
【答案】5
【解析】∵BP平分∠ABC,∴∠ABP=∠DBP,
?∵AB∥PD,∴∠ABP=∠BPD,∴∠DBP=∠BPD,∴PD=BD,同理可得PE=EC,∴△PDE的周长=PD+PE+DE=BD+EC+DE=BC=5?cm.
23.
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则_______°.
?
【答案】35
【解析】∵QC⊥OA,QD⊥OB,QC=QD,∴点Q在∠AOB的平分线上,∴,∵∠AOB=70°,∴35°.
24.
如图所示,在四边形中,,的平分线与的平分线交于点,则__________.
?
【答案】
【解析】∵的平分线与的平分线交于点,∴,,
?又∵,∴.∵在四边形中,,∴.
?∴.
三、解答题
25.
证明:角的平分线上的点到角的两边的距离相等.
【答案】解:如图,,点在上,,垂足分别为,,求证.
?证明:∵,,∴.
?在△PDO?和△PEO中,∴△PDO≌△PEO?(AAS).∴,即角的平分线上的点到角的两边的距离相等.
?
26.
如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
?求证:
?
(1)PE=PF;
【答案】连接AP,∵PE⊥AB,PF⊥AC,
?∴∠AEP=∠AFP=90°.?∵AE=AF,AP=AP,
?∴Rt△AEP≌Rt△AFP(HL),∴PE=PF.
(2)点P在∠BAC的平分线上.
【答案】由第1问知Rt△AEP≌Rt△AFP,
?∴∠EAP=∠FAP,
?∴点P在∠BAC的平分线上.
27.
如图,在△ABC中,CA=CB,,AD平分,于点E,AB=10?cm.求△BED的周长.
?
【答案】∵,,
?∴CD=DE.又∵AD=AD,∴,∴,AC=AE,∴BD+DE=BD+DC=BC.
?∵AC=CB,∴BD+DE=BC=CA=AE,∴BD+DE+BE=AE+BE=AB=10?cm,∴△BED的周长为10?cm.
28.
如图所示,,平分,.求的度数.
?
【答案】50°
【解析】∵,∴.∵平分,∴,∵,∴.
29.
如图,在△ABC中,,,CE平分,于D,于F,求的度数.?
?
【答案】∵,,,∴.
?∵CE平分,∴.
?又∵,∴,
?∴,
?∵,∴.
30.
如图所示,,分别是△ABC?的两条角平分线,且相交于点,求证点在的平分线上.
?
【答案】证明:如图,过点作,,分别垂直于,,,垂足分别为,,.∴.同理,?.∴.∴点在的平分线上.
?
31.
如图,已知F,G是OA上两点,M,N是OB上两点,且FG=MN,△PFG和△PMN的面积相等.试判断点P是否在∠AOB的平分线上,并说明理由.
?
【答案】点P在∠AOB的平分线上.
?理由:如图所示,作PD⊥OA于D,PE⊥OB于E.
?
?∵,,
?,
?∴=.
?又∵FG=MN,∴PD=PE,∴点P在∠AOB的平分线上.
32.
已知:如图所示,,于,于点,交于点.求证:平分.
?
【答案】证明:∵,,∴.
?在△BDE?和△CDF中,∴△BDE≌△CDF(AAS),∴,
?又∵,,∴平分.
33.
如图,,分别是△ABC的外角和的平分线,它们交于点,于,于,求证:为的平分线.
?
【答案】证明:如图,过点作于.∵,,,分别是和的平分线,∴,,∴.
?又∵,,∴点在的平分线上,∴为的平分线.
34.
如图所示,在中,分别延长的边,到,,与的平分线相交点,爱动脑筋的小明在写作业时发现如下规律:
?
?①若,则;
?②若,则;
?③若,则.
(1)上述规律,若,则????????;
【答案】15°
(2)请你用数学表达式归纳出与的关系;
【答案】.
(3)请说明第2题中结论的正确性.
【答案】证明:因为是的一个外角,
?所以.
?因为是的平分线,
?所以.
?同理,可得.
?因为,
?所以
?
?
?.
35.
在△ABC中,AD是的平分线.
?
(1)如图①,求证:;
【答案】证明:如图,作于E,于F.
?
?∵AD是的平分线,∴DE=DF.
?∴.
(2)如图②,若BD=CD,求证:AB=AC;
【答案】证明:∵BD=CD,∴.
?由第1问知,
?∴,∴AB=AC.
(3)如图③,若AB=5,AC=4,BC=6,求BD的长.
【答案】如图,过A作,垂足为M.
?∵,,∴,
?由第1问知,∴.又BC=6,∴.
?
36.
工人师傅常用角尺平分一个任意角,做法如下:如图,是任意一个角,在边,上分别截取,移动角尺,使角尺两边相同的刻度分别与点,重合,过角尺顶点的射线便是的平分线.请结合图形说明理由.
?
【答案】在和中,,,,∴,∴,即平分.
37.
如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:
?(1)使其到两公路的距离相等;
?(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
?
【答案】解:如图,连接,作的平分线交于点,则点就是所要建超市的位置.
?
四、证明题
38.
已知:如图,在中,,,是的平分线,求证:.
?
【答案】证明?:∵,
?∴,
?∵,
?∴,
?∴,,
?∵是的平分线,
?∴,
?∴,∴,
?在中,∵,
?∴,
?.
39.
如图,,M是BC的中点,DM平分,求证:AM平分.
?
【答案】过点M作于N.
?∵DM平分,?,
?∴CM=MM.又M是BC的中点,
?∴CM=BM,∴MN=MB.
?又∵,∴,∴AM平分.
40.
如图,,点是的中点,则平分,为什么?
?
【答案】如图,
?
?连接.点是的中点,∴.
?在和中,∵,
?∴.
?在和中,∴,
?∴,∴,∴平分.
41.
如图所示,射线OM,ON是两条公路,点A,B,C,D是四个小商店,其中A,B在公路OM上,C,D在公路ON上,且AB=CD,点P是一座购物商场,若,则商场P的位置恰好在的平分线上,为什么?
?
【答案】过点P作于点E,于点F,如图所示.
?
?∵,,,
?∴AB·PE=CD·PF.∵AB=CD,∴PE=PF.∴点P在的平分线上.
