苏科版数学八年级上册第6章【一次函数】单元同步提升训练 (word版 无答案)
文档属性
| 名称 | 苏科版数学八年级上册第6章【一次函数】单元同步提升训练 (word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 66.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 20:22:37 | ||
图片预览


文档简介
【一次函数】单元同步提升训练
一.选择题
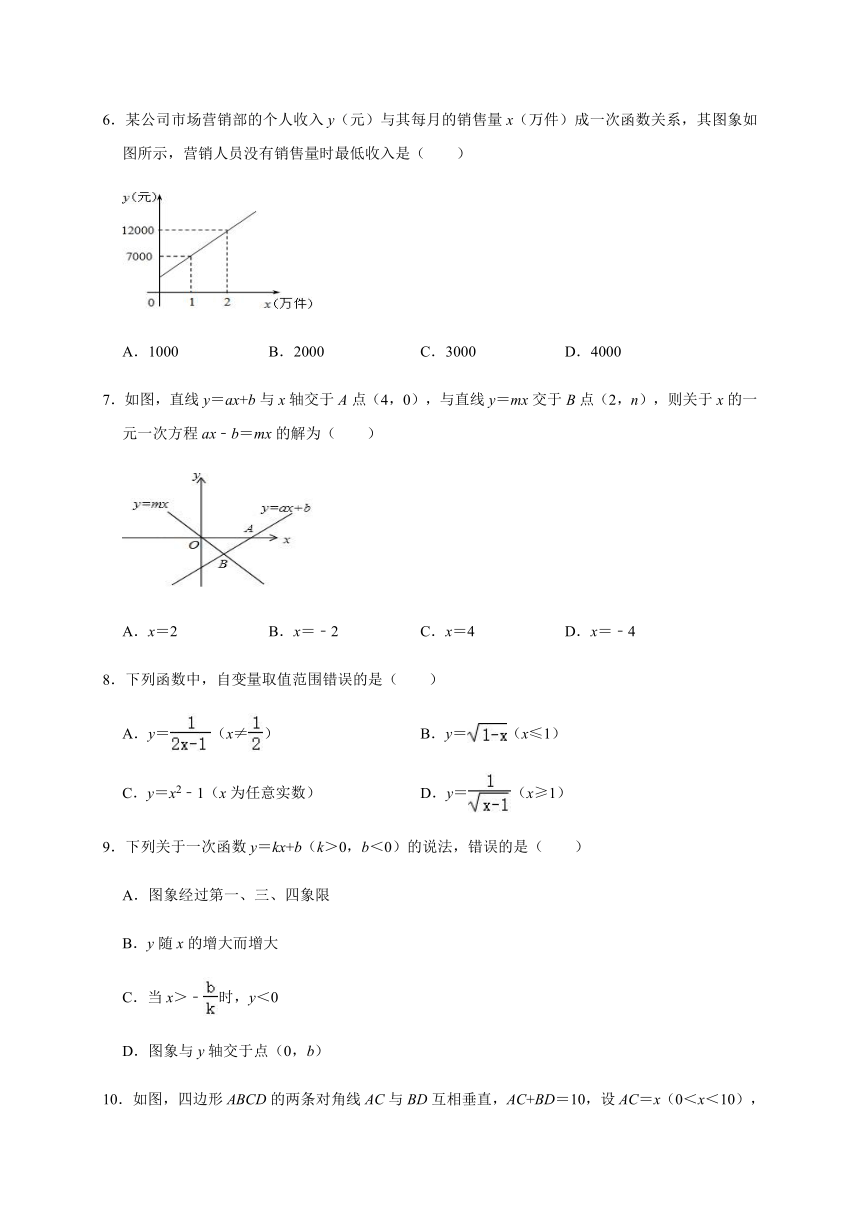
1.下列函数中,y是x的正比例函数的是( )
A.y=2x+1
B.y=3x2
C.y=x
D.y=
2.已知方程ax+b=0的解为x=﹣,则一次函数y=ax+b图象与x轴交点的横坐标为( )
A.3
B.
C.﹣2
D.
3.如图,一次函数y=kx+b的图象交y轴于点A(0,2),则不等式kx+b<2的解集为( )
A.x<0
B.x>0
C.x<﹣1
D.x>﹣1
4.直线y=kx+b与y=mx+n的交点坐标为(﹣1,1),则方程组的解是( )
A.
B.
C.
D.
5.若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A.
B.
C.
D.
6.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
7.如图,直线y=ax+b与x轴交于A点(4,0),与直线y=mx交于B点(2,n),则关于x的一元一次方程ax﹣b=mx的解为( )
A.x=2
B.x=﹣2
C.x=4
D.x=﹣4
8.下列函数中,自变量取值范围错误的是( )
A.y=(x≠)
B.y=(x≤1)
C.y=x2﹣1(x为任意实数)
D.y=(x≥1)
9.下列关于一次函数y=kx+b(k>0,b<0)的说法,错误的是( )
A.图象经过第一、三、四象限
B.y随x的增大而增大
C.当x>﹣时,y<0
D.图象与y轴交于点(0,b)
10.如图,四边形ABCD的两条对角线AC与BD互相垂直,AC+BD=10,设AC=x(0<x<10),四边形ABCD的面积为y,则y与x的函数关系式为( )
A.y=x(10﹣x)
B.y=x(10﹣x)
C.y=x(10+x)
D.y=(10﹣x)2
二.填空题
11.当m=
时,函数y=(m+1)x+5是一次函数.
12.物理学中把﹣273℃作为热力学温度的零度,热力学温度T(K)与摄氏温度t(℃)之间有如此数量关系:T=t+273,当摄氏温度为37℃时,热力学温度为
.
13.函数y=中,自变量x的取值范围为
.
14.已知函数y=(m+3)x2m﹣1+2x﹣1(x≠0)是一次函数,则m的值是
.
15.如图,一次函数y=kx+b和的图象交于点M.则关于x,y的二元一次方程组的解是
.
三.解答题
16.已知y=(m﹣2)x+|m|﹣2.
(1)m满足什么条件时,y=(m﹣2)x+|m|﹣2是一次函数?
(2)m满足什么条件时,y=(m﹣2)x+|m|﹣2是正比例函数?
17.某馆集体门票收费标准是40人以内(含40人)每人15元,超过40人的这部分每人10元.
(1)写出应收门票费y(元)与参观人数x(人)之间的函数关系式;
(2)利用(1)中的关系式计算,某班58名学生去该馆参观,购门票共花多少元钱?
18.定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的奇妙点.
(1)若方程为x2﹣7x+6=0,写出该一元二次方程的奇妙点M的坐标.
(2)若关于x的一元二次方程x2﹣(2m+1)x+2m=0(m<0)的奇妙点为M,过点M向x轴和y轴作垂线,两垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的一元二次方程x2+bx+c=0的奇妙点M始终在直线y=kx﹣2(k﹣2)的图象上,若有请算出b,c的值,若没有请说明理由.
19.我市全民健身中心面向学生推出假期游泳优惠活动,活动方案如下.
方案一:购买一张学生卡,每次游泳费用按六折优惠;
方案二:不购买学生卡,每次游泳费用按八折优惠.
设某学生假期游泳x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求y1关于x的函数关系式,并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用;
(2)求打折前的每次游泳费用和k2的值;
(3)八年级学生小明计划假期前往全民健身中心游泳8次,应选择哪种方案所需费用更少?说明理由.
20.如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;
(4)若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,清说明理由.
一.选择题
1.下列函数中,y是x的正比例函数的是( )
A.y=2x+1
B.y=3x2
C.y=x
D.y=
2.已知方程ax+b=0的解为x=﹣,则一次函数y=ax+b图象与x轴交点的横坐标为( )
A.3
B.
C.﹣2
D.
3.如图,一次函数y=kx+b的图象交y轴于点A(0,2),则不等式kx+b<2的解集为( )
A.x<0
B.x>0
C.x<﹣1
D.x>﹣1
4.直线y=kx+b与y=mx+n的交点坐标为(﹣1,1),则方程组的解是( )
A.
B.
C.
D.
5.若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A.
B.
C.
D.
6.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
7.如图,直线y=ax+b与x轴交于A点(4,0),与直线y=mx交于B点(2,n),则关于x的一元一次方程ax﹣b=mx的解为( )
A.x=2
B.x=﹣2
C.x=4
D.x=﹣4
8.下列函数中,自变量取值范围错误的是( )
A.y=(x≠)
B.y=(x≤1)
C.y=x2﹣1(x为任意实数)
D.y=(x≥1)
9.下列关于一次函数y=kx+b(k>0,b<0)的说法,错误的是( )
A.图象经过第一、三、四象限
B.y随x的增大而增大
C.当x>﹣时,y<0
D.图象与y轴交于点(0,b)
10.如图,四边形ABCD的两条对角线AC与BD互相垂直,AC+BD=10,设AC=x(0<x<10),四边形ABCD的面积为y,则y与x的函数关系式为( )
A.y=x(10﹣x)
B.y=x(10﹣x)
C.y=x(10+x)
D.y=(10﹣x)2
二.填空题
11.当m=
时,函数y=(m+1)x+5是一次函数.
12.物理学中把﹣273℃作为热力学温度的零度,热力学温度T(K)与摄氏温度t(℃)之间有如此数量关系:T=t+273,当摄氏温度为37℃时,热力学温度为
.
13.函数y=中,自变量x的取值范围为
.
14.已知函数y=(m+3)x2m﹣1+2x﹣1(x≠0)是一次函数,则m的值是
.
15.如图,一次函数y=kx+b和的图象交于点M.则关于x,y的二元一次方程组的解是
.
三.解答题
16.已知y=(m﹣2)x+|m|﹣2.
(1)m满足什么条件时,y=(m﹣2)x+|m|﹣2是一次函数?
(2)m满足什么条件时,y=(m﹣2)x+|m|﹣2是正比例函数?
17.某馆集体门票收费标准是40人以内(含40人)每人15元,超过40人的这部分每人10元.
(1)写出应收门票费y(元)与参观人数x(人)之间的函数关系式;
(2)利用(1)中的关系式计算,某班58名学生去该馆参观,购门票共花多少元钱?
18.定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的奇妙点.
(1)若方程为x2﹣7x+6=0,写出该一元二次方程的奇妙点M的坐标.
(2)若关于x的一元二次方程x2﹣(2m+1)x+2m=0(m<0)的奇妙点为M,过点M向x轴和y轴作垂线,两垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的一元二次方程x2+bx+c=0的奇妙点M始终在直线y=kx﹣2(k﹣2)的图象上,若有请算出b,c的值,若没有请说明理由.
19.我市全民健身中心面向学生推出假期游泳优惠活动,活动方案如下.
方案一:购买一张学生卡,每次游泳费用按六折优惠;
方案二:不购买学生卡,每次游泳费用按八折优惠.
设某学生假期游泳x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求y1关于x的函数关系式,并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用;
(2)求打折前的每次游泳费用和k2的值;
(3)八年级学生小明计划假期前往全民健身中心游泳8次,应选择哪种方案所需费用更少?说明理由.
20.如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;
(4)若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,清说明理由.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
