北师大版九年级下册数学《第3章 圆》单元测试题(Word版 含解析)
文档属性
| 名称 | 北师大版九年级下册数学《第3章 圆》单元测试题(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 247.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 05:57:14 | ||
图片预览



文档简介
2020-2021学年北师大新版九年级下册数学《第3章 圆》单元测试题
一.选择题
1.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
2.⊙O的半径为15,在⊙O内有一点P到圆心O的距离为9,则通过P点且长度是整数值的弦的条数是( )
A.5 B.7 C.10 D.12
3.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm B.8dm C.10dm D.12dm
4.如图,∠B=58°,则∠OCA=( )
A.25° B.30° C.32° D.20°
5.下列说法正确的是( )
A.三点确定一个圆
B.圆心角的度数等于圆周角的两倍
C.与半径垂直的直线是圆的切线
D.在同圆或等圆中,相等的圆周角所对的弦、弧分别相等
6.圆的半径为5cm,圆心到一条直线的距离是7cm,则直线与圆的公共点个数是( )
A.0个 B.1个 C.2个 D.1个或2个
7.边长为2的等边三角形的外接圆的半径是( )
A. B. C. D.
8.若一个扇形的面积是相应圆的,则它的圆心角为( )
A.150° B.120° C.90° D.60°
9.下列说法中,正确的是( )
A.经过三个点一定可以作一个圆
B.经过四个点一定可以作一个圆
C.经过圆心且平分弦的直线一定垂直于这条弦
D.三角形的外心到三角形各顶点的距离都相等
10.下面图形中,一定有内切圆的是( )
A.矩形 B.等腰梯形 C.菱形 D.平行四边形
二.填空题
11.若一扇形面积为100πcm2,此扇形所在圆半径为50cm,则扇形的圆心角度数为 °.
12.△ABC中,AB=13cm,BC=12cm,AC=5cm,以C为圆心,若要使AB与⊙C相切,则⊙C的半径应为 .
13.已知直线l:y=x﹣4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为 时,过P,A,B三点不能作出一个圆.
14.在同圆或等圆中,相等的圆心角所对的 相等,所对的 相等,所对的弦的 相等.
15.弧长的计算:如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长l= .
16.直角三角形的两条直角边长为3和4,则它的外接圆的半径R= ,内切圆半径r= .
17.已知⊙O的面积为25πcm2,⊙O所在的平面内有一点P,若OP=6.5cm,则点P在 ;若OP=4cm,则点P在 ;若OP= cm,则点P在⊙O上.
18.若直角三角形ABC的两条直角边AC、BC的长分别是5cm和12cm,则此直角三角形外接圆半径为 cm,内切圆半径为 cm.
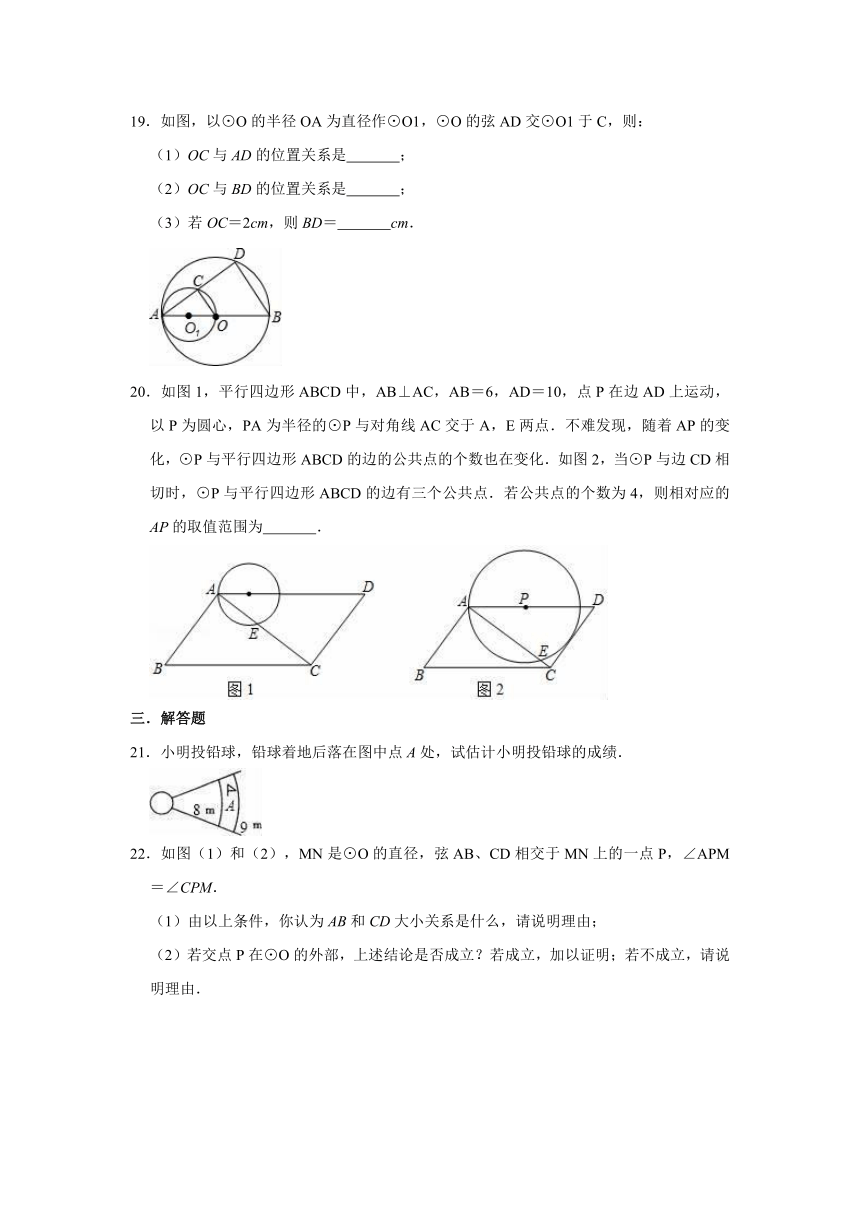
19.如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,则:
(1)OC与AD的位置关系是 ;
(2)OC与BD的位置关系是 ;
(3)若OC=2cm,则BD= cm.
20.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为 .
三.解答题
21.小明投铅球,铅球着地后落在图中点A处,试估计小明投铅球的成绩.
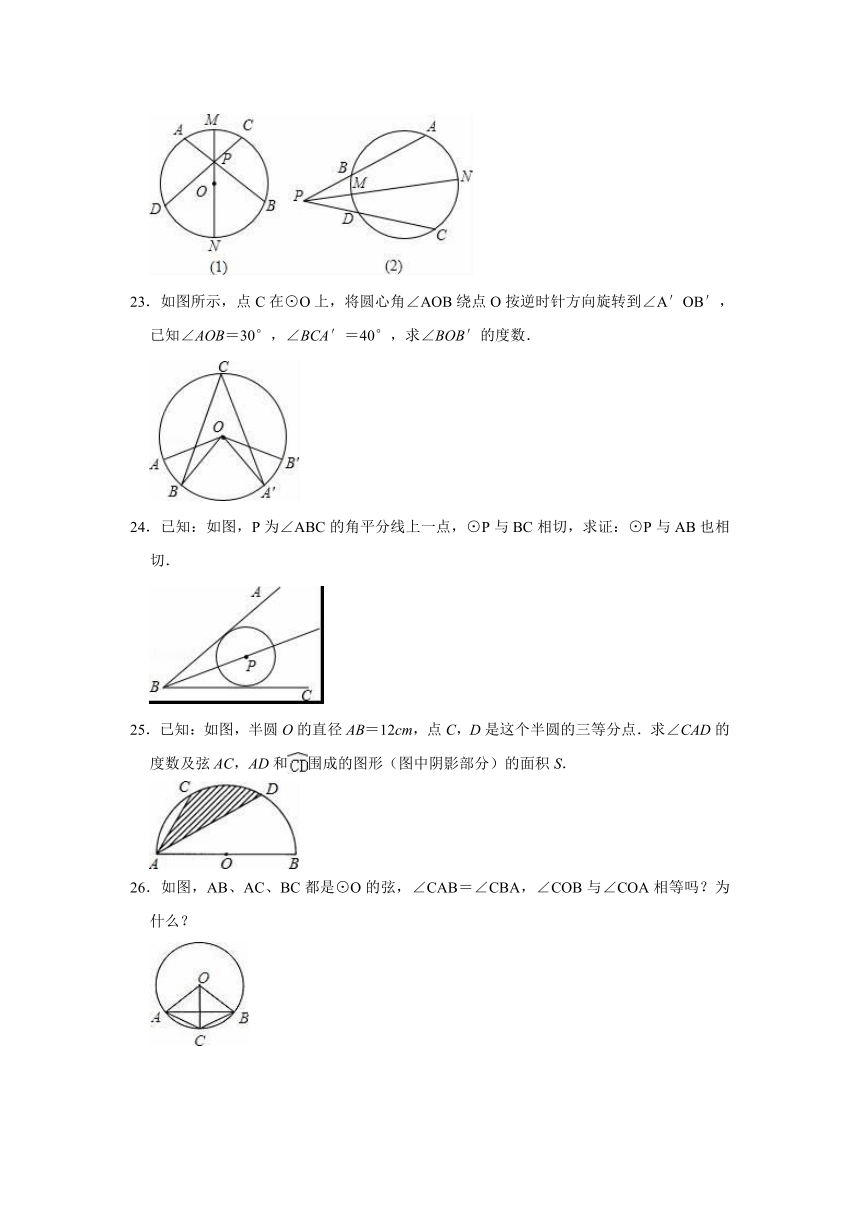
22.如图(1)和(2),MN是⊙O的直径,弦AB、CD相交于MN上的一点P,∠APM=∠CPM.
(1)由以上条件,你认为AB和CD大小关系是什么,请说明理由;
(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由.
23.如图所示,点C在⊙O上,将圆心角∠AOB绕点O按逆时针方向旋转到∠A′OB′,已知∠AOB=30°,∠BCA′=40°,求∠BOB′的度数.
24.已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切,求证:⊙P与AB也相切.
25.已知:如图,半圆O的直径AB=12cm,点C,D是这个半圆的三等分点.求∠CAD的度数及弦AC,AD和围成的图形(图中阴影部分)的面积S.
26.如图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,∠COB与∠COA相等吗?为什么?
参考答案与试题解析
一.选择题
1.解:.
故选:C.
2.解:如图,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,则AP=BP,
∵⊙O的半径为15,OP=9,
∴过P点的最长的弦是直径CD=30,
最短的弦长AB=2AP=,
∴⊙O中,过P点的弦长L的取值范围是24≤L≤30,
若L为整数,所以L的值可取24,25,26,27,28,29,30,
又根据圆的对称性知:长度为25,26,27,28,29的弦各有2条,
∴通过P点且长度是整数值的弦的条数是12.
故选:D.
3.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
4.解:连接OA,
∵∠B=58°,
∴∠AOC=2∠B=116°.
∵OA=OC,
∴∠OAC=∠OCA==32°.故选C.
5.解:A、不在同一直线上的三点确定一个圆;故A错误.
B、在同圆或等圆中,同弧或等弧所对的圆心角的度数等于圆周角的两倍;故B错误.
C、经过半径外端且垂直于半径的直线是圆的切线;故C错误.
D、在同圆或等圆中,相等的圆周角所对的弦、弧分别相等;故D正确.
故选:D.
6.解:∵圆的半径为5cm,圆心到一条直线的距离是7cm,
5<7,
即半径小于圆心到直线的距离,
∴直线与圆的位置关系是相离,
即直线与圆有0个交点.
故选:A.
7.解:连接中心和顶点,作出边心距.
那么得到直角三角形在中心的度数为:360÷3÷2=60°,
那么外接圆半径是2÷2÷sin60°=;
故选:D.
8.解:设圆的面积=πr2,则扇形面积==;
解得n=90°.
故选:C.
9.解:A选项错,正确的是不在同一直线上的三个点确定一个圆;
B选项错,经过不在一直线上的四个点不一定能做圆,除非这四点共圆;
C选项错,过圆心的直径所在的直线都平分直径(平分弦),却不一定垂直这条直径;
只有D选项正确,外心是三边垂直平分线的交点,线段垂直平分线上的点到线段两端的距离相等,所以,三角形的外心到三角形各顶点的距离都相等.
故选:D.
10.解:角平分线上的点到两边的距离相等,菱形的对角线同时也是菱形内角的平分线,所以菱形两对角线的交点到菱形各边的距离相等.以交点为圆心,距离为半径的圆就是菱形的内切圆.
故选:C.
二.填空题
11.解:∵扇形面积公式为:S=LR
∴L=
∴L=4π
∵弧长公式为:L=θR
∴θ=
∴θ=π=14.4°
故此题应该填14.4°.
12.解:设AB与⊙C相切的切点为D,即CD⊥AB(CD为△ABC斜边AB边上的高,也等于圆C的半径),
∵132=52+122,即AB2=AC2+BC2(勾股定理),
∴△ABC为直角三角形,
∵S△ABC==,
∴,
CD=,
∴⊙C的半径应为.
故答案为:.
13.解:设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,
解得,
∴y=﹣x+2.
解方程组,得,
∴当P的坐标为(3,﹣1)时,过P,A,B三点不能作出一个圆.
故答案为(3,﹣1).
14.解:根据定理可知,在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
故应填弧、弦、弦心距.
15.解:弧长的公式为:l=.
故答案为:l=.
16.解:直角三角形的两条直角边长为3和4,则其斜边为5,
所以它的外接圆半径R=×5=2.5,内切圆半径r==1.
17.解:因为圆的面积为25πcm2,所以圆的半径为5cm.
若OP=6.5cm,因为6.5cm>5cm,则点P在⊙O外;
若OP=4cm,因为4cm<5cm,则点P在⊙O内;
若OP=5cm,则点P在⊙O上.
故答案为:⊙O外;⊙O内;5.
18.解:(1)在Rt△ABC内,AB===13(cm)
∵AB是Rt△ABC外接圆的直径
∴Rt△ABC外接圆的半径为6.5(cm)
(2)设Rt△ABC内切圆P的半径为r.
AE=AM=AC﹣r=5﹣r,BE=BN=BC﹣r=12﹣r
AB=AE+BE=(5﹣r)+(12﹣r)=17﹣2r
∴13=17﹣2r,即r=2
故答案为6.5,2.
19.解:(1)∵以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,
∴∠ACO=∠ADB=90°,
∴OC⊥AC,
即OC⊥AD;
∴OC与AD的位置关系是:垂直;
(2)∵∠ACO=∠ADB=90°,
∴OC∥BD;
∴OC与BD的位置关系是:平行;
(3)∵OA=OB,OC∥BD,
∴AC=CD,
∴BD=2OC=2×2=4(cm).
故答案为:(1)垂直,(2)平行,(3)4.
20.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S?ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
三.解答题
21.解:在8m和9m之间.
22.(1)解:AB=CD,
理由是:过O作OE⊥AB于E,OF⊥CD于F,连接OB、OD,
∵∠APM=∠CPM,∠APM=∠BPN,∠CPM=∠DPN,
∴∠BPN=∠DPN,
∵OE⊥AB,OF⊥CD,
∴OE=OF,
在Rt△BEO和Rt△DOF中,OF=OE,OD=OB,由勾股定理得:BE=DF,
∵OF⊥CD,OE⊥AB,
OF、OE过O,
∴由垂径定理得:CD=2DF,AB=2BE,
∴AB=CD.
(2)AB=CD成立,
证明:过O作OE⊥AB于E,OF⊥CD于F,连接OB、OD,
∵∠APM=∠CPM,
∴OE=OF,
在Rt△BEO和Rt△DOF中,OF=OE,OD=OB,由勾股定理得:BE=DF,
∵OF⊥CD,OE⊥AB,
OF、OE过O,
∴由垂径定理得:CD=2DF,AB=2BE,
∴AB=CD.
23.解:∵∠BCA′=40°,
∴∠BOA′=2∠BCA′=80°,
∵点C在⊙O上,将圆心角∠AOB绕点O按逆时针方向旋转到∠A′OB′,
∴∠A′OB′=∠AOB=30°,
∴∠BOB′=∠BOA′+∠A′OB′=110°.
24.证明:过P点分别作AB、BC的垂线PE、PD,
∵P为∠ABC的角平分线上一点,
∴PE=PD,
∵⊙P与BC相切,
∴PD为⊙P的半径,
∴PE也是⊙P的半径,
∵PE⊥AB,
∴⊙P与AB也相切.
25.解:连接CO、OD,CD,
∵C、D是这个半圆的三等分点,
∴CD∥AB,∠COD=60°,
∴∠CAD的度数为:30°,
∵OC=OD,∴△OCD是等边三角形,CD=OC=AB=6,
∴△OCD与△CDA是等底等高的三角形,
∴S阴影=S扇形OCD=π×62=6πcm2.
答:阴影部分的面积S是6πcm2.
26.解:∠COB=∠COA,
理由是:∵∠CAB=∠CBA,∴AC=BC,
∴弧AC=弧BC,∴∠COB=∠COA.
一.选择题
1.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
2.⊙O的半径为15,在⊙O内有一点P到圆心O的距离为9,则通过P点且长度是整数值的弦的条数是( )
A.5 B.7 C.10 D.12
3.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm B.8dm C.10dm D.12dm
4.如图,∠B=58°,则∠OCA=( )
A.25° B.30° C.32° D.20°
5.下列说法正确的是( )
A.三点确定一个圆
B.圆心角的度数等于圆周角的两倍
C.与半径垂直的直线是圆的切线
D.在同圆或等圆中,相等的圆周角所对的弦、弧分别相等
6.圆的半径为5cm,圆心到一条直线的距离是7cm,则直线与圆的公共点个数是( )
A.0个 B.1个 C.2个 D.1个或2个
7.边长为2的等边三角形的外接圆的半径是( )
A. B. C. D.
8.若一个扇形的面积是相应圆的,则它的圆心角为( )
A.150° B.120° C.90° D.60°
9.下列说法中,正确的是( )
A.经过三个点一定可以作一个圆
B.经过四个点一定可以作一个圆
C.经过圆心且平分弦的直线一定垂直于这条弦
D.三角形的外心到三角形各顶点的距离都相等
10.下面图形中,一定有内切圆的是( )
A.矩形 B.等腰梯形 C.菱形 D.平行四边形
二.填空题
11.若一扇形面积为100πcm2,此扇形所在圆半径为50cm,则扇形的圆心角度数为 °.
12.△ABC中,AB=13cm,BC=12cm,AC=5cm,以C为圆心,若要使AB与⊙C相切,则⊙C的半径应为 .
13.已知直线l:y=x﹣4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为 时,过P,A,B三点不能作出一个圆.
14.在同圆或等圆中,相等的圆心角所对的 相等,所对的 相等,所对的弦的 相等.
15.弧长的计算:如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长l= .
16.直角三角形的两条直角边长为3和4,则它的外接圆的半径R= ,内切圆半径r= .
17.已知⊙O的面积为25πcm2,⊙O所在的平面内有一点P,若OP=6.5cm,则点P在 ;若OP=4cm,则点P在 ;若OP= cm,则点P在⊙O上.
18.若直角三角形ABC的两条直角边AC、BC的长分别是5cm和12cm,则此直角三角形外接圆半径为 cm,内切圆半径为 cm.
19.如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,则:
(1)OC与AD的位置关系是 ;
(2)OC与BD的位置关系是 ;
(3)若OC=2cm,则BD= cm.
20.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为 .
三.解答题
21.小明投铅球,铅球着地后落在图中点A处,试估计小明投铅球的成绩.
22.如图(1)和(2),MN是⊙O的直径,弦AB、CD相交于MN上的一点P,∠APM=∠CPM.
(1)由以上条件,你认为AB和CD大小关系是什么,请说明理由;
(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由.
23.如图所示,点C在⊙O上,将圆心角∠AOB绕点O按逆时针方向旋转到∠A′OB′,已知∠AOB=30°,∠BCA′=40°,求∠BOB′的度数.
24.已知:如图,P为∠ABC的角平分线上一点,⊙P与BC相切,求证:⊙P与AB也相切.
25.已知:如图,半圆O的直径AB=12cm,点C,D是这个半圆的三等分点.求∠CAD的度数及弦AC,AD和围成的图形(图中阴影部分)的面积S.
26.如图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,∠COB与∠COA相等吗?为什么?
参考答案与试题解析
一.选择题
1.解:.
故选:C.
2.解:如图,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,则AP=BP,
∵⊙O的半径为15,OP=9,
∴过P点的最长的弦是直径CD=30,
最短的弦长AB=2AP=,
∴⊙O中,过P点的弦长L的取值范围是24≤L≤30,
若L为整数,所以L的值可取24,25,26,27,28,29,30,
又根据圆的对称性知:长度为25,26,27,28,29的弦各有2条,
∴通过P点且长度是整数值的弦的条数是12.
故选:D.
3.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
4.解:连接OA,
∵∠B=58°,
∴∠AOC=2∠B=116°.
∵OA=OC,
∴∠OAC=∠OCA==32°.故选C.
5.解:A、不在同一直线上的三点确定一个圆;故A错误.
B、在同圆或等圆中,同弧或等弧所对的圆心角的度数等于圆周角的两倍;故B错误.
C、经过半径外端且垂直于半径的直线是圆的切线;故C错误.
D、在同圆或等圆中,相等的圆周角所对的弦、弧分别相等;故D正确.
故选:D.
6.解:∵圆的半径为5cm,圆心到一条直线的距离是7cm,
5<7,
即半径小于圆心到直线的距离,
∴直线与圆的位置关系是相离,
即直线与圆有0个交点.
故选:A.
7.解:连接中心和顶点,作出边心距.
那么得到直角三角形在中心的度数为:360÷3÷2=60°,
那么外接圆半径是2÷2÷sin60°=;
故选:D.
8.解:设圆的面积=πr2,则扇形面积==;
解得n=90°.
故选:C.
9.解:A选项错,正确的是不在同一直线上的三个点确定一个圆;
B选项错,经过不在一直线上的四个点不一定能做圆,除非这四点共圆;
C选项错,过圆心的直径所在的直线都平分直径(平分弦),却不一定垂直这条直径;
只有D选项正确,外心是三边垂直平分线的交点,线段垂直平分线上的点到线段两端的距离相等,所以,三角形的外心到三角形各顶点的距离都相等.
故选:D.
10.解:角平分线上的点到两边的距离相等,菱形的对角线同时也是菱形内角的平分线,所以菱形两对角线的交点到菱形各边的距离相等.以交点为圆心,距离为半径的圆就是菱形的内切圆.
故选:C.
二.填空题
11.解:∵扇形面积公式为:S=LR
∴L=
∴L=4π
∵弧长公式为:L=θR
∴θ=
∴θ=π=14.4°
故此题应该填14.4°.
12.解:设AB与⊙C相切的切点为D,即CD⊥AB(CD为△ABC斜边AB边上的高,也等于圆C的半径),
∵132=52+122,即AB2=AC2+BC2(勾股定理),
∴△ABC为直角三角形,
∵S△ABC==,
∴,
CD=,
∴⊙C的半径应为.
故答案为:.
13.解:设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,
解得,
∴y=﹣x+2.
解方程组,得,
∴当P的坐标为(3,﹣1)时,过P,A,B三点不能作出一个圆.
故答案为(3,﹣1).
14.解:根据定理可知,在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
故应填弧、弦、弦心距.
15.解:弧长的公式为:l=.
故答案为:l=.
16.解:直角三角形的两条直角边长为3和4,则其斜边为5,
所以它的外接圆半径R=×5=2.5,内切圆半径r==1.
17.解:因为圆的面积为25πcm2,所以圆的半径为5cm.
若OP=6.5cm,因为6.5cm>5cm,则点P在⊙O外;
若OP=4cm,因为4cm<5cm,则点P在⊙O内;
若OP=5cm,则点P在⊙O上.
故答案为:⊙O外;⊙O内;5.
18.解:(1)在Rt△ABC内,AB===13(cm)
∵AB是Rt△ABC外接圆的直径
∴Rt△ABC外接圆的半径为6.5(cm)
(2)设Rt△ABC内切圆P的半径为r.
AE=AM=AC﹣r=5﹣r,BE=BN=BC﹣r=12﹣r
AB=AE+BE=(5﹣r)+(12﹣r)=17﹣2r
∴13=17﹣2r,即r=2
故答案为6.5,2.
19.解:(1)∵以⊙O的半径OA为直径作⊙O1,⊙O的弦AD交⊙O1于C,
∴∠ACO=∠ADB=90°,
∴OC⊥AC,
即OC⊥AD;
∴OC与AD的位置关系是:垂直;
(2)∵∠ACO=∠ADB=90°,
∴OC∥BD;
∴OC与BD的位置关系是:平行;
(3)∵OA=OB,OC∥BD,
∴AC=CD,
∴BD=2OC=2×2=4(cm).
故答案为:(1)垂直,(2)平行,(3)4.
20.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S?ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
三.解答题
21.解:在8m和9m之间.
22.(1)解:AB=CD,
理由是:过O作OE⊥AB于E,OF⊥CD于F,连接OB、OD,
∵∠APM=∠CPM,∠APM=∠BPN,∠CPM=∠DPN,
∴∠BPN=∠DPN,
∵OE⊥AB,OF⊥CD,
∴OE=OF,
在Rt△BEO和Rt△DOF中,OF=OE,OD=OB,由勾股定理得:BE=DF,
∵OF⊥CD,OE⊥AB,
OF、OE过O,
∴由垂径定理得:CD=2DF,AB=2BE,
∴AB=CD.
(2)AB=CD成立,
证明:过O作OE⊥AB于E,OF⊥CD于F,连接OB、OD,
∵∠APM=∠CPM,
∴OE=OF,
在Rt△BEO和Rt△DOF中,OF=OE,OD=OB,由勾股定理得:BE=DF,
∵OF⊥CD,OE⊥AB,
OF、OE过O,
∴由垂径定理得:CD=2DF,AB=2BE,
∴AB=CD.
23.解:∵∠BCA′=40°,
∴∠BOA′=2∠BCA′=80°,
∵点C在⊙O上,将圆心角∠AOB绕点O按逆时针方向旋转到∠A′OB′,
∴∠A′OB′=∠AOB=30°,
∴∠BOB′=∠BOA′+∠A′OB′=110°.
24.证明:过P点分别作AB、BC的垂线PE、PD,
∵P为∠ABC的角平分线上一点,
∴PE=PD,
∵⊙P与BC相切,
∴PD为⊙P的半径,
∴PE也是⊙P的半径,
∵PE⊥AB,
∴⊙P与AB也相切.
25.解:连接CO、OD,CD,
∵C、D是这个半圆的三等分点,
∴CD∥AB,∠COD=60°,
∴∠CAD的度数为:30°,
∵OC=OD,∴△OCD是等边三角形,CD=OC=AB=6,
∴△OCD与△CDA是等底等高的三角形,
∴S阴影=S扇形OCD=π×62=6πcm2.
答:阴影部分的面积S是6πcm2.
26.解:∠COB=∠COA,
理由是:∵∠CAB=∠CBA,∴AC=BC,
∴弧AC=弧BC,∴∠COB=∠COA.
