北师大版九年级下册数学 3.4圆周角和圆心角之间的关系 同步练习 (word版 含解析)
文档属性
| 名称 | 北师大版九年级下册数学 3.4圆周角和圆心角之间的关系 同步练习 (word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 20:15:00 | ||
图片预览

文档简介
3.4圆周角和圆心角之间的关系 同步练习
一.选择题
1.如图,AB是⊙O的直径,AC是弦,若∠ACO=30°,则sin∠COB的等于( )
A. B. C. D.
2.⊙O中,∠AOB=100°,若C是上一点,则∠ACB等于( )
A.80° B.100° C.120° D.130°
3.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于( )
A.50° B.60° C.70° D.75°
4.如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若的度数是40°,则的度数是( )
A.10° B.15° C.20° D.25°
5.AB为半圆O的直径,弦AD,BC相交于点P,若CD=3,AB=4,则tan∠BPD等于( )
A. B. C. D.
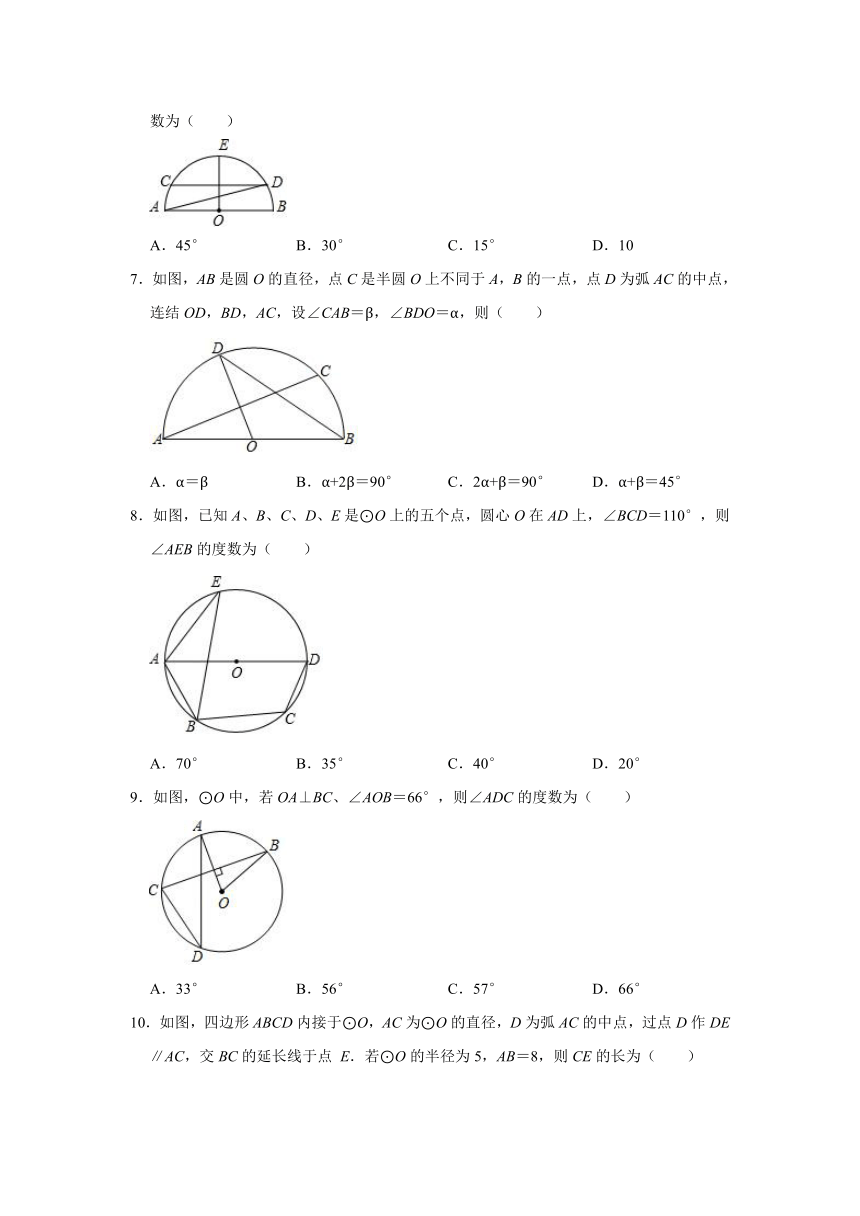
6.如图所示,AB是直径,点E是弧AB中点,弦CD∥AB且平分OE,连AD,∠BAD度数为( )
A.45° B.30° C.15° D.10
7.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β B.α+2β=90° C.2α+β=90° D.α+β=45°
8.如图,已知A、B、C、D、E是⊙O上的五个点,圆心O在AD上,∠BCD=110°,则∠AEB的度数为( )
A.70° B.35° C.40° D.20°
9.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为( )
A.33° B.56° C.57° D.66°
10.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为弧AC的中点,过点D作DE∥AC,交BC的延长线于点 E.若⊙O的半径为5,AB=8,则CE的长为( )
A.4 B. C. D.
二.填空题
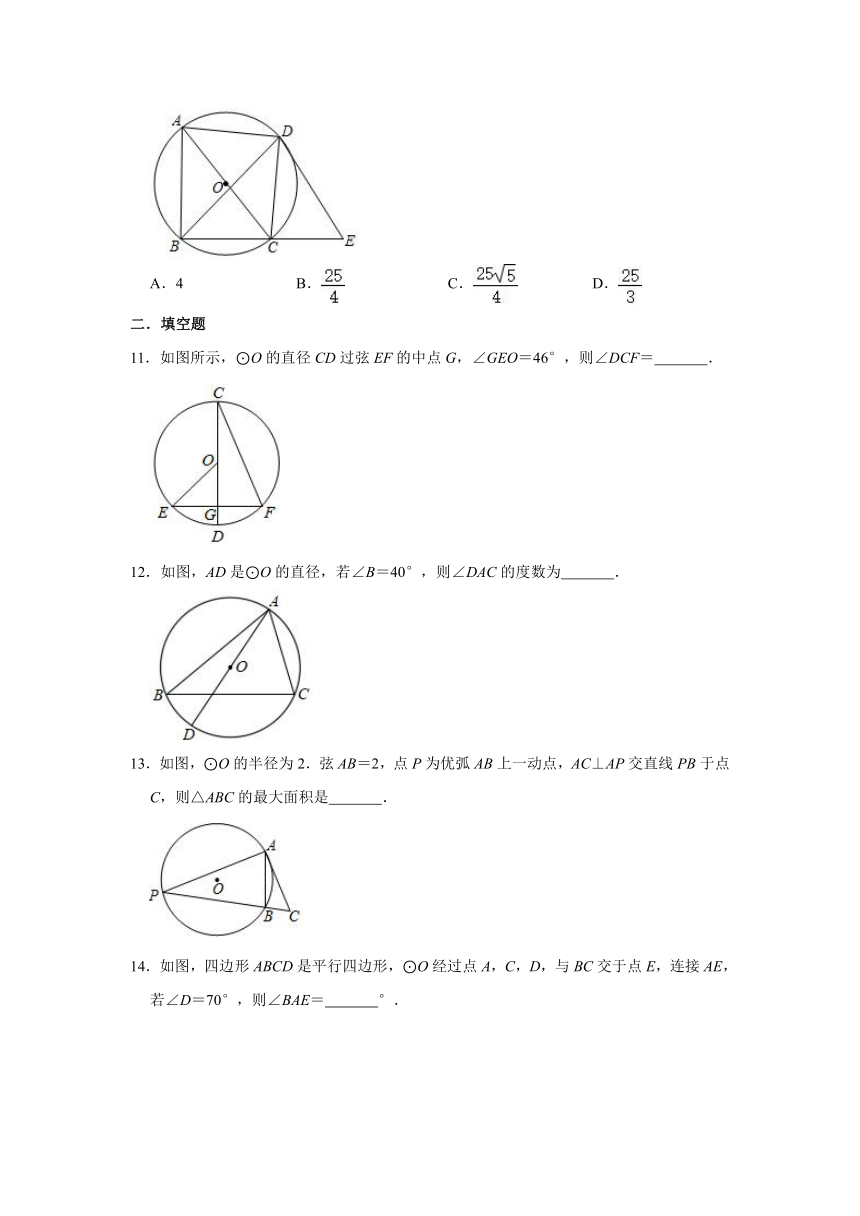
11.如图所示,⊙O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF= .
12.如图,AD是⊙O的直径,若∠B=40°,则∠DAC的度数为 .
13.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是 .
14.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=70°,则∠BAE= °.
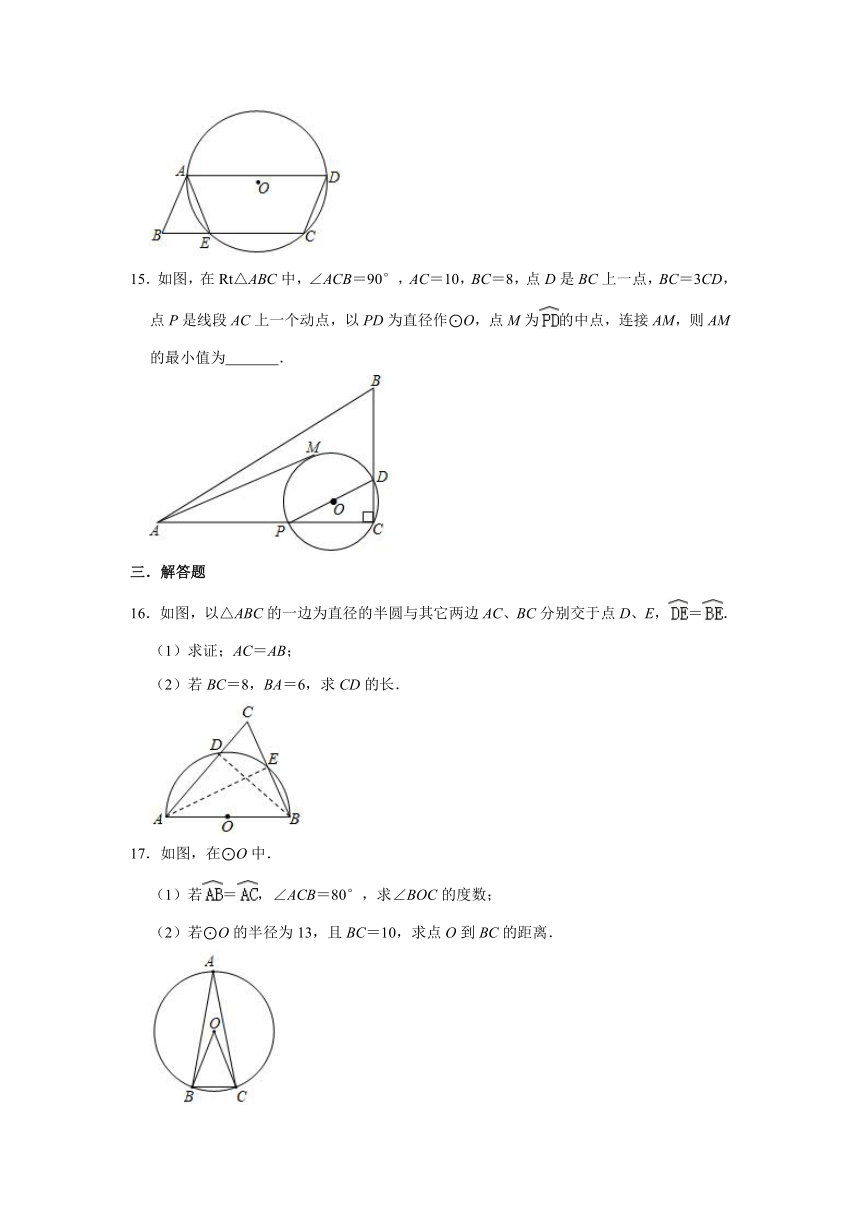
15.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM的最小值为 .
三.解答题
16.如图,以△ABC的一边为直径的半圆与其它两边AC、BC分别交于点D、E,=.
(1)求证;AC=AB;
(2)若BC=8,BA=6,求CD的长.
17.如图,在⊙O中.
(1)若=,∠ACB=80°,求∠BOC的度数;
(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.
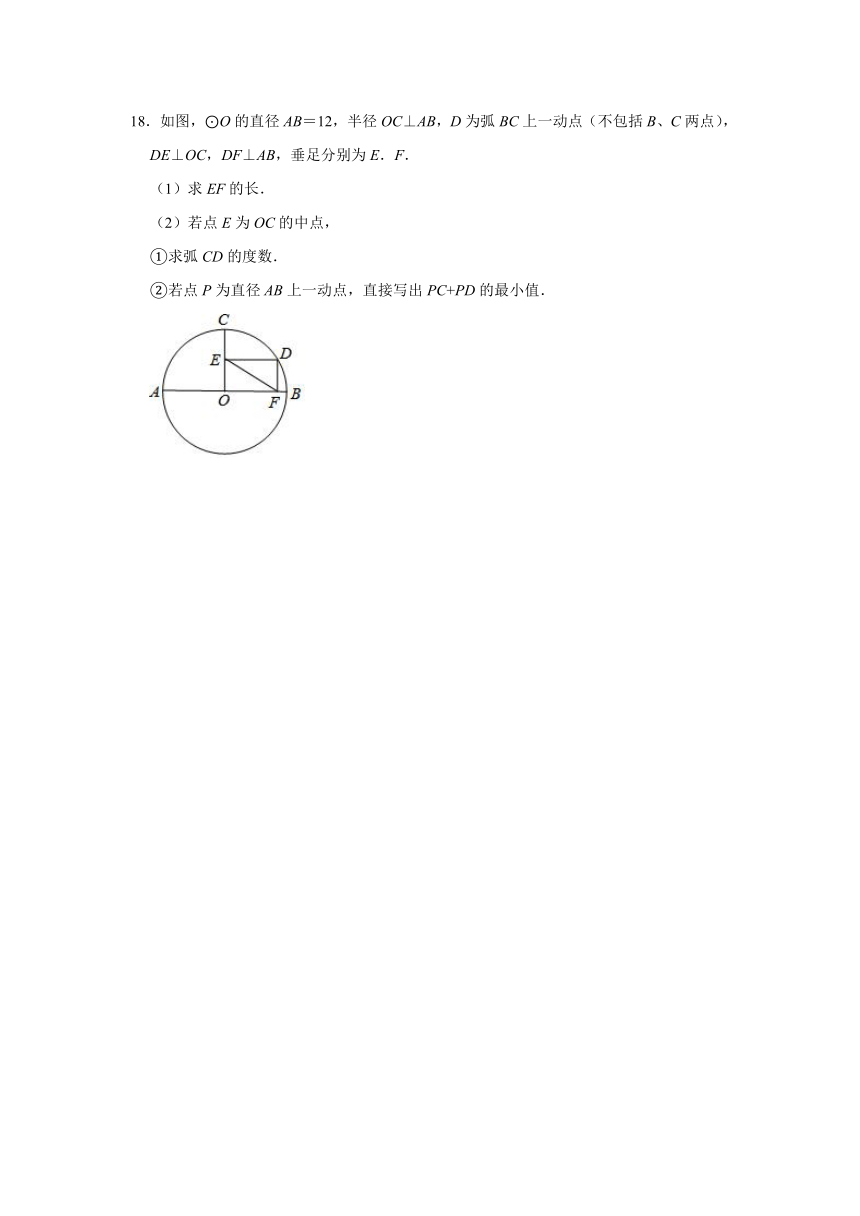
18.如图,⊙O的直径AB=12,半径OC⊥AB,D为弧BC上一动点(不包括B、C两点),DE⊥OC,DF⊥AB,垂足分别为E.F.
(1)求EF的长.
(2)若点E为OC的中点,
①求弧CD的度数.
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
参考答案
一.选择题
1.解:∵OA=OC,∠ACO=30°,
∴∠OAC=∠ACO=30°,
∵∠COB是△AOC的外角,
∴∠COB=∠ACO+∠OAC=60°,
∴sin∠COB=sin60°=.
故选:C.
2.解:如图:在优弧上取点D,连接AD,BD,
∵⊙O中,∠AOB=100°,
∴∠ADB=∠AOB=50°,
∵四边形ACBD是⊙O的内接四边形,
∴∠ACB=180°﹣∠ADB=130°.
故选:D.
3.解:连接OA,OB,OC,OD,
∵∠BAD=50°,==,
∴∠BOD=2∠BAD=100°,
∵==,
∴AOB=∠BOC=∠COD=∠BOD=50°,
∴∠AOD=∠AOB+∠BOC+∠COD=150°,
∴∠AED=∠AOD=75°.
故选:D.
4.解:∵的度数是40°,
∴∠ACM=40°
∵∠CBP=∠CAP=10°,
∴A、C、P、B四点共圆,
∴∠ACM=∠ABP=40°,
∵∠CPB=10°,
∴∠ABC=40°﹣10°=30°,
∵AC=BC,
∴∠CAB=∠ABC=30°,
∴∠ACB=120°,
∴∠BCN=180°﹣∠ACM﹣∠ACB=20°,
∴的度数是20°.
故选:C.
5.解:连接BD.
则∠CDA=∠ABC.(同圆中同弧AC所对的圆周角相等)
同理∠DCB=∠DAB,
所以△PCD∽△PAB,
==.
∵AB直径,
∴∠ADB=90°.
∴∠PDB=∠ADB=90°,
在Rt△PDB中,
cos∠DPB==,
∴sin∠DPB=. (sin2∠DPB+cos2∠DPB=1)
tan∠BPD==.
故选:A.
6.解:设CD与OE交于P,则连接OC,∵CD∥AB且平分OE,∴OP=?OC,
∴sin∠PCO=,
∴∠PCO=30°,
又∵CD∥AB,∴∠COA=∠PCO=30°,
∴∠BAD=∠BOD=15°.
故选:C.
7.解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
8.解:如图,连接DE,
∵四边形BCDE是⊙O的内接四边形,
∴∠BCD+∠BED=180°,
∵∠BCD=110°,
∴∠BED=70°,
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEB=∠AED﹣∠BED=90°﹣70°=20°,
故选:D.
9.解:如图,连接OC,OB.
∵OA⊥BC,
∴=,
∴∠AOC=∠AOB=66°,
∴∠ADC=∠AOC=33°,
故选:A.
10.解:∵⊙O的半径为5,
∴AC=10,
∴AD=CD=5,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB=8,
∴BC=6,
∵∠BAD=∠DCE,
∵∠ABD=∠CDE=45°,
∴△ABD∽△CDE,
∴,
∴,
∴CE=,
故选:B.
二.填空题
11.解:∵CD是直径,EG=GF,
∴CD⊥EF,
∴=,
∴∠CDF=∠EOD,
∵∠OGE=90°,∠GEO=46°,
∴∠EOD=44°,
∴∠DCF=22°.
故答案为:22°.
12.解:连接CD.
∵AD是直径,
∴∠ACD=90°,
∵∠D=∠B=40°,
∴∠DAC=90°﹣40°=50°.
故答案为50°.
13.解:连结OA、OB,作△ABC的外接圆D,如图1,
∵OA=OB=2,AB=2,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,如图2,
当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,
∴△ABC的最大面积为.
故答案为:.
14.解:∵四边形ABCD是平行四边形,∠D=70°,
∴∠DCB=(180°﹣∠D)=110°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=70°,∠B=180°﹣∠BCD=70°
∴∠BAE=180°﹣70°﹣70°=40°,
故答案为:40
15.解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.
∵=,
∴OM⊥PD,
∴∠MOD=90°,
∴∠MCD=∠MOD=45°,
∵∠ACB=90°,
∴∠ACT=45°,
∵AT⊥CT,
∴∠ATC=90°,
∵AC=10,
∴AT=AC?sin45°=5,
∵AM≥AT,
∴AM≥5,
∴AM的最小值为5,
故答案为5.
三.解答题
16.(1)证明:∵=,
∴∠CAE=∠BAE,
∵AB为直径,
∴∠AEB=90°,
∵∠ABE+∠BAE=90°,∠C+∠CAE=90°,
∴∠ABC=∠C,
∴AC=AB;
(2)解:∵∠CAE=∠CBD,∠ACE=∠BCD,
∴△CAE∽△CBD,
∴=,即=,
∴CD=.
17.解:(1)∵=,
∴∠ABC=∠ACB=80°,
∴∠A=180°﹣80°﹣80°=20°,
∴∠BOC=2∠A=40°;
(2)作OH⊥BC于H,如图,则BH=CH=BC=5,
在Rt△OBH中,OH===12,
即点O到BC的距离为12.
18.解:(1)连接OD,
∵⊙O的直径AB=12,
∴圆的半径为12÷2=6,
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=6;
(2)①∵点E为OC的中点,
∴OE=OC=OD,
∴∠EDO=30°,
∴∠DOE=60°,
∴弧CD的度数为60°;
②延长CO交⊙O于G,l连接DG交AB于P,
则PC+PD的最小值=DG,
∵∠G=∠COD=30°,
∵EG=9,
∴DG===6,
∴PC+PD的最小值为6.
一.选择题
1.如图,AB是⊙O的直径,AC是弦,若∠ACO=30°,则sin∠COB的等于( )
A. B. C. D.
2.⊙O中,∠AOB=100°,若C是上一点,则∠ACB等于( )
A.80° B.100° C.120° D.130°
3.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于( )
A.50° B.60° C.70° D.75°
4.如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若的度数是40°,则的度数是( )
A.10° B.15° C.20° D.25°
5.AB为半圆O的直径,弦AD,BC相交于点P,若CD=3,AB=4,则tan∠BPD等于( )
A. B. C. D.
6.如图所示,AB是直径,点E是弧AB中点,弦CD∥AB且平分OE,连AD,∠BAD度数为( )
A.45° B.30° C.15° D.10
7.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β B.α+2β=90° C.2α+β=90° D.α+β=45°
8.如图,已知A、B、C、D、E是⊙O上的五个点,圆心O在AD上,∠BCD=110°,则∠AEB的度数为( )
A.70° B.35° C.40° D.20°
9.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为( )
A.33° B.56° C.57° D.66°
10.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为弧AC的中点,过点D作DE∥AC,交BC的延长线于点 E.若⊙O的半径为5,AB=8,则CE的长为( )
A.4 B. C. D.
二.填空题
11.如图所示,⊙O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF= .
12.如图,AD是⊙O的直径,若∠B=40°,则∠DAC的度数为 .
13.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是 .
14.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=70°,则∠BAE= °.
15.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM的最小值为 .
三.解答题
16.如图,以△ABC的一边为直径的半圆与其它两边AC、BC分别交于点D、E,=.
(1)求证;AC=AB;
(2)若BC=8,BA=6,求CD的长.
17.如图,在⊙O中.
(1)若=,∠ACB=80°,求∠BOC的度数;
(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.
18.如图,⊙O的直径AB=12,半径OC⊥AB,D为弧BC上一动点(不包括B、C两点),DE⊥OC,DF⊥AB,垂足分别为E.F.
(1)求EF的长.
(2)若点E为OC的中点,
①求弧CD的度数.
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
参考答案
一.选择题
1.解:∵OA=OC,∠ACO=30°,
∴∠OAC=∠ACO=30°,
∵∠COB是△AOC的外角,
∴∠COB=∠ACO+∠OAC=60°,
∴sin∠COB=sin60°=.
故选:C.
2.解:如图:在优弧上取点D,连接AD,BD,
∵⊙O中,∠AOB=100°,
∴∠ADB=∠AOB=50°,
∵四边形ACBD是⊙O的内接四边形,
∴∠ACB=180°﹣∠ADB=130°.
故选:D.
3.解:连接OA,OB,OC,OD,
∵∠BAD=50°,==,
∴∠BOD=2∠BAD=100°,
∵==,
∴AOB=∠BOC=∠COD=∠BOD=50°,
∴∠AOD=∠AOB+∠BOC+∠COD=150°,
∴∠AED=∠AOD=75°.
故选:D.
4.解:∵的度数是40°,
∴∠ACM=40°
∵∠CBP=∠CAP=10°,
∴A、C、P、B四点共圆,
∴∠ACM=∠ABP=40°,
∵∠CPB=10°,
∴∠ABC=40°﹣10°=30°,
∵AC=BC,
∴∠CAB=∠ABC=30°,
∴∠ACB=120°,
∴∠BCN=180°﹣∠ACM﹣∠ACB=20°,
∴的度数是20°.
故选:C.
5.解:连接BD.
则∠CDA=∠ABC.(同圆中同弧AC所对的圆周角相等)
同理∠DCB=∠DAB,
所以△PCD∽△PAB,
==.
∵AB直径,
∴∠ADB=90°.
∴∠PDB=∠ADB=90°,
在Rt△PDB中,
cos∠DPB==,
∴sin∠DPB=. (sin2∠DPB+cos2∠DPB=1)
tan∠BPD==.
故选:A.
6.解:设CD与OE交于P,则连接OC,∵CD∥AB且平分OE,∴OP=?OC,
∴sin∠PCO=,
∴∠PCO=30°,
又∵CD∥AB,∴∠COA=∠PCO=30°,
∴∠BAD=∠BOD=15°.
故选:C.
7.解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
8.解:如图,连接DE,
∵四边形BCDE是⊙O的内接四边形,
∴∠BCD+∠BED=180°,
∵∠BCD=110°,
∴∠BED=70°,
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEB=∠AED﹣∠BED=90°﹣70°=20°,
故选:D.
9.解:如图,连接OC,OB.
∵OA⊥BC,
∴=,
∴∠AOC=∠AOB=66°,
∴∠ADC=∠AOC=33°,
故选:A.
10.解:∵⊙O的半径为5,
∴AC=10,
∴AD=CD=5,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB=8,
∴BC=6,
∵∠BAD=∠DCE,
∵∠ABD=∠CDE=45°,
∴△ABD∽△CDE,
∴,
∴,
∴CE=,
故选:B.
二.填空题
11.解:∵CD是直径,EG=GF,
∴CD⊥EF,
∴=,
∴∠CDF=∠EOD,
∵∠OGE=90°,∠GEO=46°,
∴∠EOD=44°,
∴∠DCF=22°.
故答案为:22°.
12.解:连接CD.
∵AD是直径,
∴∠ACD=90°,
∵∠D=∠B=40°,
∴∠DAC=90°﹣40°=50°.
故答案为50°.
13.解:连结OA、OB,作△ABC的外接圆D,如图1,
∵OA=OB=2,AB=2,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,如图2,
当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,
∴△ABC的最大面积为.
故答案为:.
14.解:∵四边形ABCD是平行四边形,∠D=70°,
∴∠DCB=(180°﹣∠D)=110°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=70°,∠B=180°﹣∠BCD=70°
∴∠BAE=180°﹣70°﹣70°=40°,
故答案为:40
15.解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.
∵=,
∴OM⊥PD,
∴∠MOD=90°,
∴∠MCD=∠MOD=45°,
∵∠ACB=90°,
∴∠ACT=45°,
∵AT⊥CT,
∴∠ATC=90°,
∵AC=10,
∴AT=AC?sin45°=5,
∵AM≥AT,
∴AM≥5,
∴AM的最小值为5,
故答案为5.
三.解答题
16.(1)证明:∵=,
∴∠CAE=∠BAE,
∵AB为直径,
∴∠AEB=90°,
∵∠ABE+∠BAE=90°,∠C+∠CAE=90°,
∴∠ABC=∠C,
∴AC=AB;
(2)解:∵∠CAE=∠CBD,∠ACE=∠BCD,
∴△CAE∽△CBD,
∴=,即=,
∴CD=.
17.解:(1)∵=,
∴∠ABC=∠ACB=80°,
∴∠A=180°﹣80°﹣80°=20°,
∴∠BOC=2∠A=40°;
(2)作OH⊥BC于H,如图,则BH=CH=BC=5,
在Rt△OBH中,OH===12,
即点O到BC的距离为12.
18.解:(1)连接OD,
∵⊙O的直径AB=12,
∴圆的半径为12÷2=6,
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=6;
(2)①∵点E为OC的中点,
∴OE=OC=OD,
∴∠EDO=30°,
∴∠DOE=60°,
∴弧CD的度数为60°;
②延长CO交⊙O于G,l连接DG交AB于P,
则PC+PD的最小值=DG,
∵∠G=∠COD=30°,
∵EG=9,
∴DG===6,
∴PC+PD的最小值为6.
