人教版七年级数学下学期《5.4 平移》 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版七年级数学下学期《5.4 平移》 同步练习(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 10:01:03 | ||
图片预览


文档简介
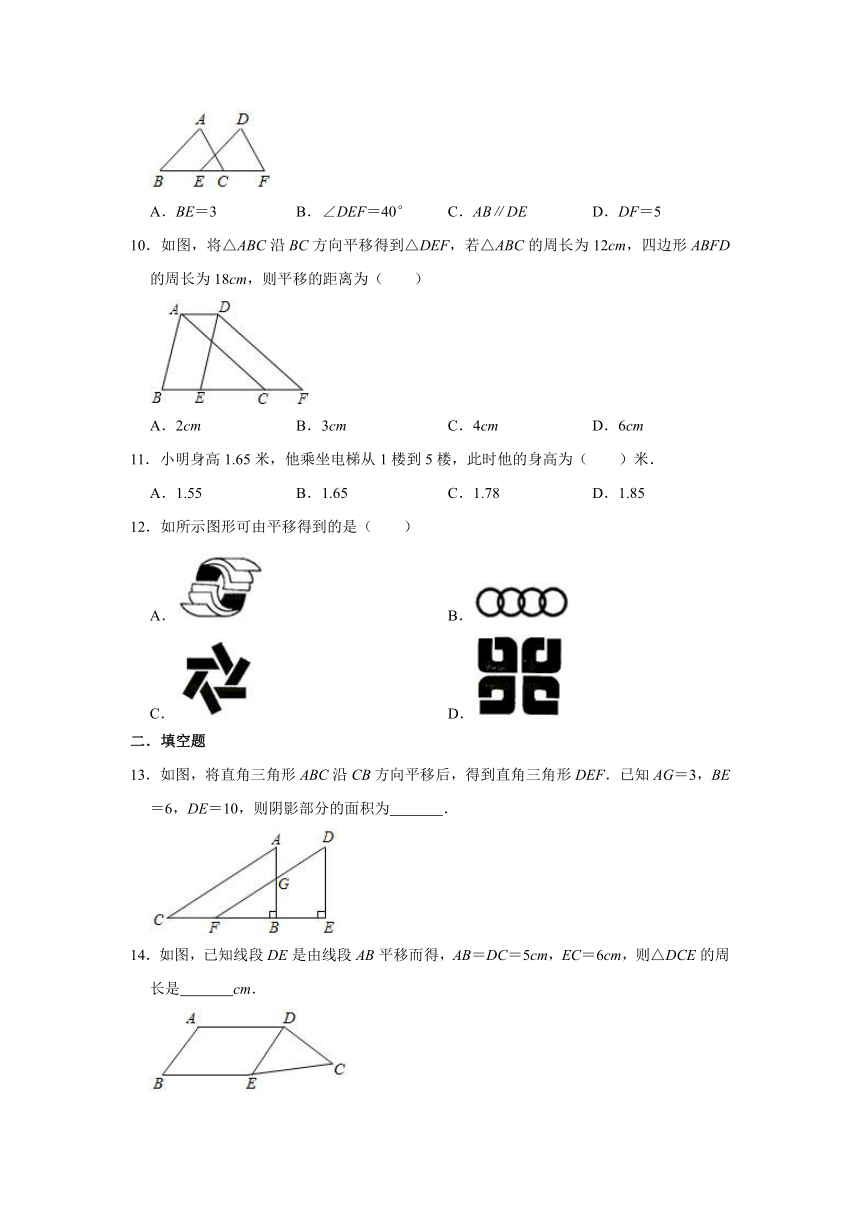
5.4 平移
一.选择题
1.如图,哪一个图可以由如图平移得到( )
A. B. C. D.
2.如图,该图形的周长为( )
A.20cm B.16cm C.14cm D.10cm
3.下列运动属于平移的是( )
A.电风扇扇叶的转动
B.石头从山顶滚到山脚的运动
C.电梯从一楼运动到三楼
D.荡秋千
4.下列现象属于数学中的平移的是( )
A.树叶从树上随风飘落
B.升降电梯由一楼升到顶楼
C.汽车方向盘的转动
D.“神舟”号卫星绕地球运动
5.中国上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”.通过平移,可将图中的吉祥物“海宝”平移到图( )
A. B.
C. D.
6.下列现象中是平移的是( )
A.翻开书中的每一页纸张
B.飞碟的快速转动
C.将一张纸沿它的中线折叠
D.电梯的上下移动
7.如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
8.如图,已知∠AEF=∠DFE,EH⊥FH于点H,EG平分∠AEF,平移EH恰好到GF,连接EG,则下列结论:①AB∥CD;②EG=HF;③EH平分∠BEF,FH平分∠EFD;④∠GFH=90°.其中正确的结论个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图,在三角形ABC中,BC=5,∠B=40°,把三角形ABC沿BC方向平移,得到三角形DEF.若CF=3,则下列结论中错误的是( )
A.BE=3 B.∠DEF=40° C.AB∥DE D.DF=5
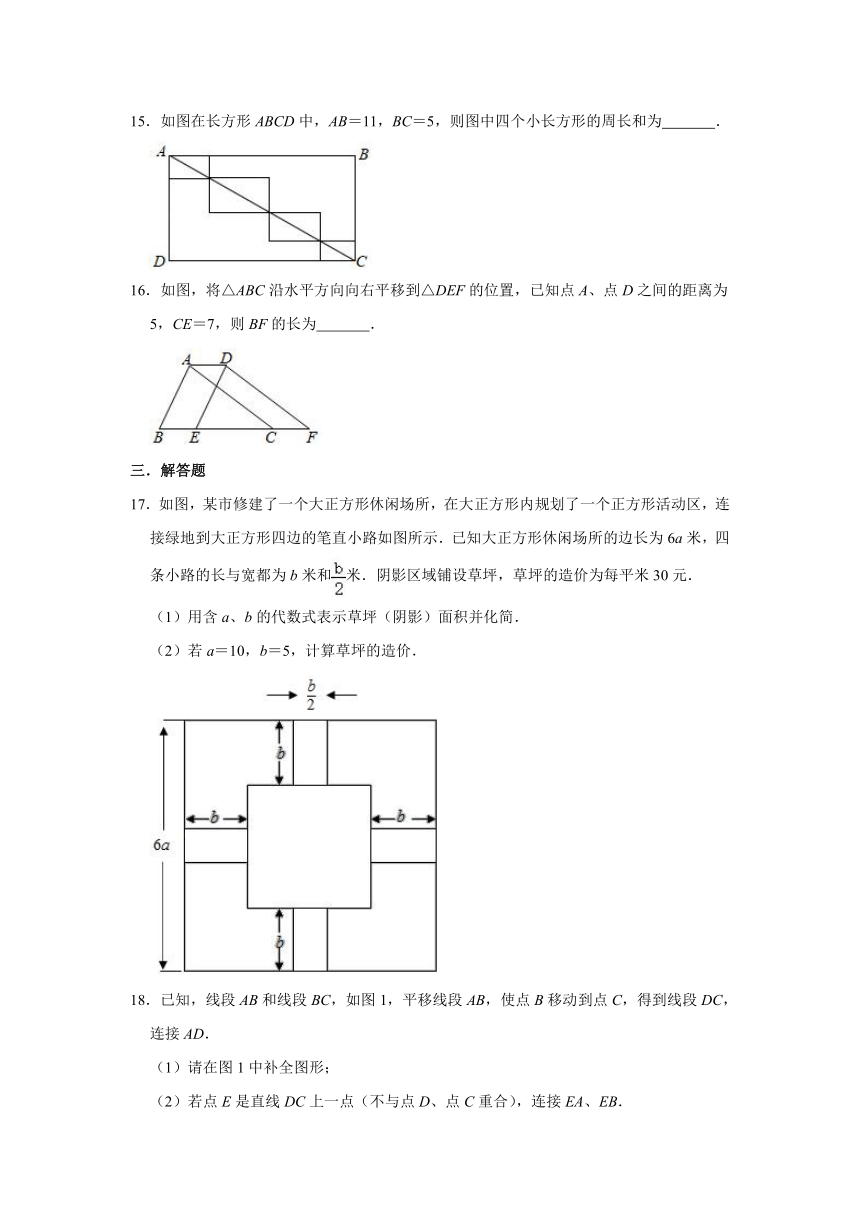
10.如图,将△ABC沿BC方向平移得到△DEF,若△ABC的周长为12cm,四边形ABFD的周长为18cm,则平移的距离为( )
A.2cm B.3cm C.4cm D.6cm
11.小明身高1.65米,他乘坐电梯从1楼到5楼,此时他的身高为( )米.
A.1.55 B.1.65 C.1.78 D.1.85
12.如所示图形可由平移得到的是( )
A. B.
C. D.
二.填空题
13.如图,将直角三角形ABC沿CB方向平移后,得到直角三角形DEF.已知AG=3,BE=6,DE=10,则阴影部分的面积为 .
14.如图,已知线段DE是由线段AB平移而得,AB=DC=5cm,EC=6cm,则△DCE的周长是 cm.
15.如图在长方形ABCD中,AB=11,BC=5,则图中四个小长方形的周长和为 .
16.如图,将△ABC沿水平方向向右平移到△DEF的位置,已知点A、点D之间的距离为5,CE=7,则BF的长为 .
三.解答题
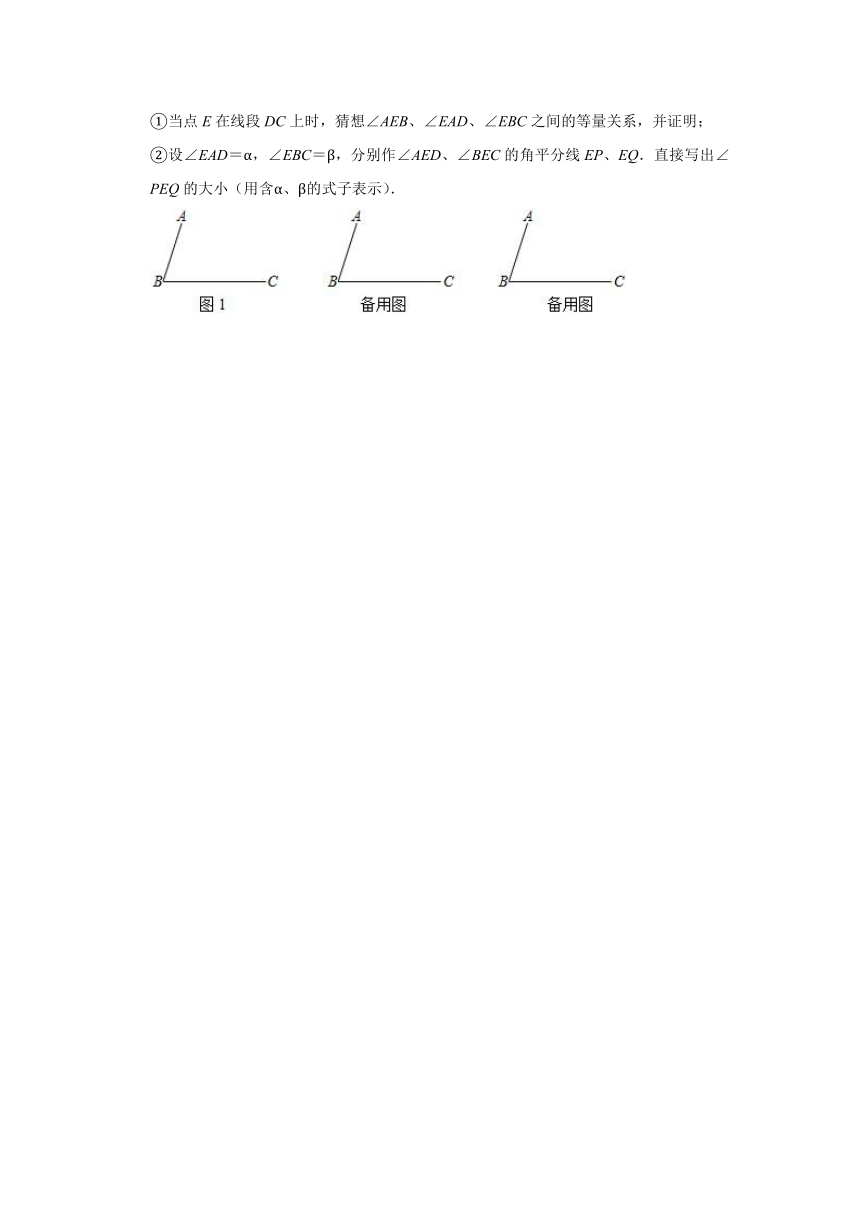
17.如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.
(1)用含a、b的代数式表示草坪(阴影)面积并化简.
(2)若a=10,b=5,计算草坪的造价.
18.已知,线段AB和线段BC,如图1,平移线段AB,使点B移动到点C,得到线段DC,连接AD.
(1)请在图1中补全图形;
(2)若点E是直线DC上一点(不与点D、点C重合),连接EA、EB.
①当点E在线段DC上时,猜想∠AEB、∠EAD、∠EBC之间的等量关系,并证明;
②设∠EAD=α,∠EBC=β,分别作∠AED、∠BEC的角平分线EP、EQ.直接写出∠PEQ的大小(用含α、β的式子表示).
参考答案
一.选择题
1.解:D选项中的图形可由题中图形平移得到.
故选:D.
2.解:该图形的周长为(6+4)×2=20(cm),
故选:A.
3.解:A.电风扇扇叶的转动不是平移,故A选项不符合题意;
B.石头从山顶滚到山脚的运动不是平移,故B选项不符合题意;
C.电梯从一楼运动到三楼是平移,故C选项符合题意;
D.荡秋千不是平移,故D选项不符合题意;
故选:C.
4.解:A、树叶从树上随风飘落不属于平移,故此选项不合题意;
B、升降电梯由一楼升到顶楼属于平移,故此选项符合题意;
C、汽车方向盘的转动属于旋转,故此选项不合题意;
D、“神舟”号卫星绕地球运动属于旋转,故此选项不合题意;
故选:B.
5.解:通过平移,可将图中的吉祥物“海宝”平移到图B,
故选:B.
6.解:A不是沿某一直线方向移动,不属于平移.B不是沿某一直线方向移动,不属于平移.C新图形与原图形的形状和大小不同,不属于平移.因此C错误.
故选:D.
7.解:因为将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,
所以:①BH∥EF,正确;
②AD=BE,正确;
③由已知条件得不出BD=CH,错误;
④∠C=∠BHD,正确;
⑤阴影部分的面积为6cm2.正确;
故选:D.
8.解:∵∠AEF=∠DFE,
∴AB∥CD,故①正确,
∵EG平分∠AEF,
∴∠AEG=∠GEF=∠AEF,
由平移知,FG∥EH,FG=EH,
∴四边形EGFH是平行四边形,
∴EG∥FH,EG=HF;故②正确;
∴∠GEF=∠EFH,
∵AB∥CD,
∴∠AEF=∠DFE,
∵∠GEF=∠AEF,
∴∠EFH=∠EFD,
∴FH平分∠EFD;
故③正确;
∵EH⊥FH,
∴∠EHF=90°,
∵四边形EGFH是平行四边形,
∴四边形EGFH是矩形,
∴∠GFH=90°,故④正确,
∴正确的结论有4个,
故选:A.
9.解:由平移的性质可知,EF=BC=5,
∵CF=3,
∴EC=EF﹣CF=2,
∴BE=BC﹣EC=3,A选项结论正确,不符合题意;
∠DEF=∠B=40°,B选项结论正确,不符合题意;
AB∥DE,C选项结论正确,不符合题意;
DF与AC相等,当不一定与BC相等,
∴DF不一定等于5,D选项说法错误,符合题意;
故选:D.
10.解:∵△ABC沿BC方向平移得到△DEF,
∴AD=BE=CF,AC=DF,
∵△ABC的周长为12cm,四边形ABFD的周长为18cm,
∴AB+BC+AC=12,AB+BF+DF+AD=18,
∴AB+BC+CF+AC+CF=18,
即12+2CF=18,解得CF=3,
∴平移的距离为3cm.
故选:B.
11.解:身高1.65米的小明乘电梯从1楼上升到5楼,则此时小明的身高为1.65米,
故选:B.
12.解:A.图形可以由旋转得到,不合题意;
B.图形可由平移得到,符合题意;
C.图形可以由旋转得到,不合题意;
D.图形可以由翻折得到,不合题意;
故选:B.
二.填空题
13.解:由平移的性质知,AB=DE=10,S△ABC=S△DEF,
∵△GBF为△ABC和△DEF的公共部分,
∴S阴影部分=S梯形DEBG,
∵∠E=90°,
∴BE是梯形DEBG的高;
∵BG=AB﹣AG=10﹣3=7,
∴S阴影部分=S梯形DEBG=×(7+10)×6=51.
故答案为:51.
14.解:∵线段DE是由线段AB平移而得,
∴DE=AB=5cm,
∴△DCE的周长=DE+CE+CD=5+5+6=16(cm).
答:△DCE的周长是16cm.
故答案为:16.
15.解:(11+5)×2=32,
故答案为:32.
16.解:∵△ABC沿水平方向向右平移到△DEF的位置,
∴BE=CF=AD=5,
∴BF=5+5+7=17.
故答案为17.
三.解答题
17.解:(1)∵阴影部分的面积为:大正方形的面积减去4个长方形的面积再减去中间小正方形的面积,
∴草坪(阴影)面积为:6a×6a﹣4×b××b﹣(6a﹣2b)2,
∴草坪(阴影)面积为:6b×(4a﹣b).
(2)草坪的造价为:6×5×(40﹣5)×30=31500(元),
故答案为:(1)6b×(4a﹣b);
(2)31500元.
18.解:(1)图形如图所示:
(2)①如图1中,过点E作EF∥AD,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴AD∥EF∥BC,
∴∠AEF=∠DAE,∠BEF=∠EBC,
∴∠AEB=∠AEF+∠BEF=∠EAD+∠EBC.
②如图1﹣1中,当点E在线段CD上时,
∵PE平分∠AED,QE平分∠BEC,
∴∠PEQ=∠AEB+(∠AED+∠BEC)=α+β+(180°﹣α﹣β)=90°+α+β.
如图1﹣2中,当点E在DC的延长线上时,
∵∠AEB=∠EAD﹣∠EBC=α﹣β,
∵PE平分∠AED,QE平分∠BEC,
∴∠PEQ=(∠BEC﹣∠AED)=α﹣β.
当点E在CD的延长线上时,同法可得∠PEQ=β﹣α.
一.选择题
1.如图,哪一个图可以由如图平移得到( )
A. B. C. D.
2.如图,该图形的周长为( )
A.20cm B.16cm C.14cm D.10cm
3.下列运动属于平移的是( )
A.电风扇扇叶的转动
B.石头从山顶滚到山脚的运动
C.电梯从一楼运动到三楼
D.荡秋千
4.下列现象属于数学中的平移的是( )
A.树叶从树上随风飘落
B.升降电梯由一楼升到顶楼
C.汽车方向盘的转动
D.“神舟”号卫星绕地球运动
5.中国上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”.通过平移,可将图中的吉祥物“海宝”平移到图( )
A. B.
C. D.
6.下列现象中是平移的是( )
A.翻开书中的每一页纸张
B.飞碟的快速转动
C.将一张纸沿它的中线折叠
D.电梯的上下移动
7.如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
8.如图,已知∠AEF=∠DFE,EH⊥FH于点H,EG平分∠AEF,平移EH恰好到GF,连接EG,则下列结论:①AB∥CD;②EG=HF;③EH平分∠BEF,FH平分∠EFD;④∠GFH=90°.其中正确的结论个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图,在三角形ABC中,BC=5,∠B=40°,把三角形ABC沿BC方向平移,得到三角形DEF.若CF=3,则下列结论中错误的是( )
A.BE=3 B.∠DEF=40° C.AB∥DE D.DF=5
10.如图,将△ABC沿BC方向平移得到△DEF,若△ABC的周长为12cm,四边形ABFD的周长为18cm,则平移的距离为( )
A.2cm B.3cm C.4cm D.6cm
11.小明身高1.65米,他乘坐电梯从1楼到5楼,此时他的身高为( )米.
A.1.55 B.1.65 C.1.78 D.1.85
12.如所示图形可由平移得到的是( )
A. B.
C. D.
二.填空题
13.如图,将直角三角形ABC沿CB方向平移后,得到直角三角形DEF.已知AG=3,BE=6,DE=10,则阴影部分的面积为 .
14.如图,已知线段DE是由线段AB平移而得,AB=DC=5cm,EC=6cm,则△DCE的周长是 cm.
15.如图在长方形ABCD中,AB=11,BC=5,则图中四个小长方形的周长和为 .
16.如图,将△ABC沿水平方向向右平移到△DEF的位置,已知点A、点D之间的距离为5,CE=7,则BF的长为 .
三.解答题
17.如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.
(1)用含a、b的代数式表示草坪(阴影)面积并化简.
(2)若a=10,b=5,计算草坪的造价.
18.已知,线段AB和线段BC,如图1,平移线段AB,使点B移动到点C,得到线段DC,连接AD.
(1)请在图1中补全图形;
(2)若点E是直线DC上一点(不与点D、点C重合),连接EA、EB.
①当点E在线段DC上时,猜想∠AEB、∠EAD、∠EBC之间的等量关系,并证明;
②设∠EAD=α,∠EBC=β,分别作∠AED、∠BEC的角平分线EP、EQ.直接写出∠PEQ的大小(用含α、β的式子表示).
参考答案
一.选择题
1.解:D选项中的图形可由题中图形平移得到.
故选:D.
2.解:该图形的周长为(6+4)×2=20(cm),
故选:A.
3.解:A.电风扇扇叶的转动不是平移,故A选项不符合题意;
B.石头从山顶滚到山脚的运动不是平移,故B选项不符合题意;
C.电梯从一楼运动到三楼是平移,故C选项符合题意;
D.荡秋千不是平移,故D选项不符合题意;
故选:C.
4.解:A、树叶从树上随风飘落不属于平移,故此选项不合题意;
B、升降电梯由一楼升到顶楼属于平移,故此选项符合题意;
C、汽车方向盘的转动属于旋转,故此选项不合题意;
D、“神舟”号卫星绕地球运动属于旋转,故此选项不合题意;
故选:B.
5.解:通过平移,可将图中的吉祥物“海宝”平移到图B,
故选:B.
6.解:A不是沿某一直线方向移动,不属于平移.B不是沿某一直线方向移动,不属于平移.C新图形与原图形的形状和大小不同,不属于平移.因此C错误.
故选:D.
7.解:因为将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,
所以:①BH∥EF,正确;
②AD=BE,正确;
③由已知条件得不出BD=CH,错误;
④∠C=∠BHD,正确;
⑤阴影部分的面积为6cm2.正确;
故选:D.
8.解:∵∠AEF=∠DFE,
∴AB∥CD,故①正确,
∵EG平分∠AEF,
∴∠AEG=∠GEF=∠AEF,
由平移知,FG∥EH,FG=EH,
∴四边形EGFH是平行四边形,
∴EG∥FH,EG=HF;故②正确;
∴∠GEF=∠EFH,
∵AB∥CD,
∴∠AEF=∠DFE,
∵∠GEF=∠AEF,
∴∠EFH=∠EFD,
∴FH平分∠EFD;
故③正确;
∵EH⊥FH,
∴∠EHF=90°,
∵四边形EGFH是平行四边形,
∴四边形EGFH是矩形,
∴∠GFH=90°,故④正确,
∴正确的结论有4个,
故选:A.
9.解:由平移的性质可知,EF=BC=5,
∵CF=3,
∴EC=EF﹣CF=2,
∴BE=BC﹣EC=3,A选项结论正确,不符合题意;
∠DEF=∠B=40°,B选项结论正确,不符合题意;
AB∥DE,C选项结论正确,不符合题意;
DF与AC相等,当不一定与BC相等,
∴DF不一定等于5,D选项说法错误,符合题意;
故选:D.
10.解:∵△ABC沿BC方向平移得到△DEF,
∴AD=BE=CF,AC=DF,
∵△ABC的周长为12cm,四边形ABFD的周长为18cm,
∴AB+BC+AC=12,AB+BF+DF+AD=18,
∴AB+BC+CF+AC+CF=18,
即12+2CF=18,解得CF=3,
∴平移的距离为3cm.
故选:B.
11.解:身高1.65米的小明乘电梯从1楼上升到5楼,则此时小明的身高为1.65米,
故选:B.
12.解:A.图形可以由旋转得到,不合题意;
B.图形可由平移得到,符合题意;
C.图形可以由旋转得到,不合题意;
D.图形可以由翻折得到,不合题意;
故选:B.
二.填空题
13.解:由平移的性质知,AB=DE=10,S△ABC=S△DEF,
∵△GBF为△ABC和△DEF的公共部分,
∴S阴影部分=S梯形DEBG,
∵∠E=90°,
∴BE是梯形DEBG的高;
∵BG=AB﹣AG=10﹣3=7,
∴S阴影部分=S梯形DEBG=×(7+10)×6=51.
故答案为:51.
14.解:∵线段DE是由线段AB平移而得,
∴DE=AB=5cm,
∴△DCE的周长=DE+CE+CD=5+5+6=16(cm).
答:△DCE的周长是16cm.
故答案为:16.
15.解:(11+5)×2=32,
故答案为:32.
16.解:∵△ABC沿水平方向向右平移到△DEF的位置,
∴BE=CF=AD=5,
∴BF=5+5+7=17.
故答案为17.
三.解答题
17.解:(1)∵阴影部分的面积为:大正方形的面积减去4个长方形的面积再减去中间小正方形的面积,
∴草坪(阴影)面积为:6a×6a﹣4×b××b﹣(6a﹣2b)2,
∴草坪(阴影)面积为:6b×(4a﹣b).
(2)草坪的造价为:6×5×(40﹣5)×30=31500(元),
故答案为:(1)6b×(4a﹣b);
(2)31500元.
18.解:(1)图形如图所示:
(2)①如图1中,过点E作EF∥AD,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴AD∥EF∥BC,
∴∠AEF=∠DAE,∠BEF=∠EBC,
∴∠AEB=∠AEF+∠BEF=∠EAD+∠EBC.
②如图1﹣1中,当点E在线段CD上时,
∵PE平分∠AED,QE平分∠BEC,
∴∠PEQ=∠AEB+(∠AED+∠BEC)=α+β+(180°﹣α﹣β)=90°+α+β.
如图1﹣2中,当点E在DC的延长线上时,
∵∠AEB=∠EAD﹣∠EBC=α﹣β,
∵PE平分∠AED,QE平分∠BEC,
∴∠PEQ=(∠BEC﹣∠AED)=α﹣β.
当点E在CD的延长线上时,同法可得∠PEQ=β﹣α.
