人教版数学八年级下册18.1.1 平行四边形的性质 练习试卷(Word版含答案)
文档属性
| 名称 | 人教版数学八年级下册18.1.1 平行四边形的性质 练习试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:39:39 | ||
图片预览



文档简介
18.1.1《平行四边形的性质》精选练习
一、选择题
1.下列命题中,是真命题的是(??? )
A.平行四边形的对角线一定相等
B.等腰三角形任意一条边上的高线、中线和角平分线都三线合一
C.三角形的中位线平行于第三边并且等于它的一半
D.三角形的两边之和小于第三边
2.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2??? B.1:3??? C.1:4??? D.1:5
3.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E, 且AE=3,则AB的长为(? )
A.4???? ??? B.3 ??? ??? C.2.5??? ??? D.2???
4.如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5????? B.6????? C.4????? D.5
5.如图,将?ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为( )
A.102°????? B.112°????? C.122°????? D.92°
6.已知平行四边形的一边长为14,下列各组数据中能分别作为它的两条对角线的长的是( )
A.10与16 ??B.12与16??? ???C.20与22 ????D.10与40
7.如图,A、B两点被一座山隔开,M、N分别是AC、BC中点,测量MN的长度为40m,那么AB的长度为( )
A.40m??? B.80m???? C.160m????? D.不能确定
8.平行四边形ABCD与等边三角形AEF按如图所示的方式摆放,如果∠B=45°,则∠BAE的大小是( )
A.75°?? ??B.80°??? ?C.100°? ???D.120°
9.如图,四边形ABCD是平行四边形,点A、B、C的坐标分别为(2,0)、(0,1)、(1,2),则AB+BC的值为( )
A.???? B.3?????? C.4?????? D.5
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC=14,则EF的长是 (??? )
A.2??????????? B.3????????? C.4??????????? D.5
11.如图所示,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3,则AC的长是( )
A.12???? B.14????? C.16???? D.18
12.如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,2AB=BC,连接OE.
下列结论:①∠CAD=30°;②S?ABCD=AB·AC;③OB=AB;④4OE=BC.成立的个数有( ? ?)
A.1个?? ? B.2个??? C.3个? ? D.4个
二 、填空题
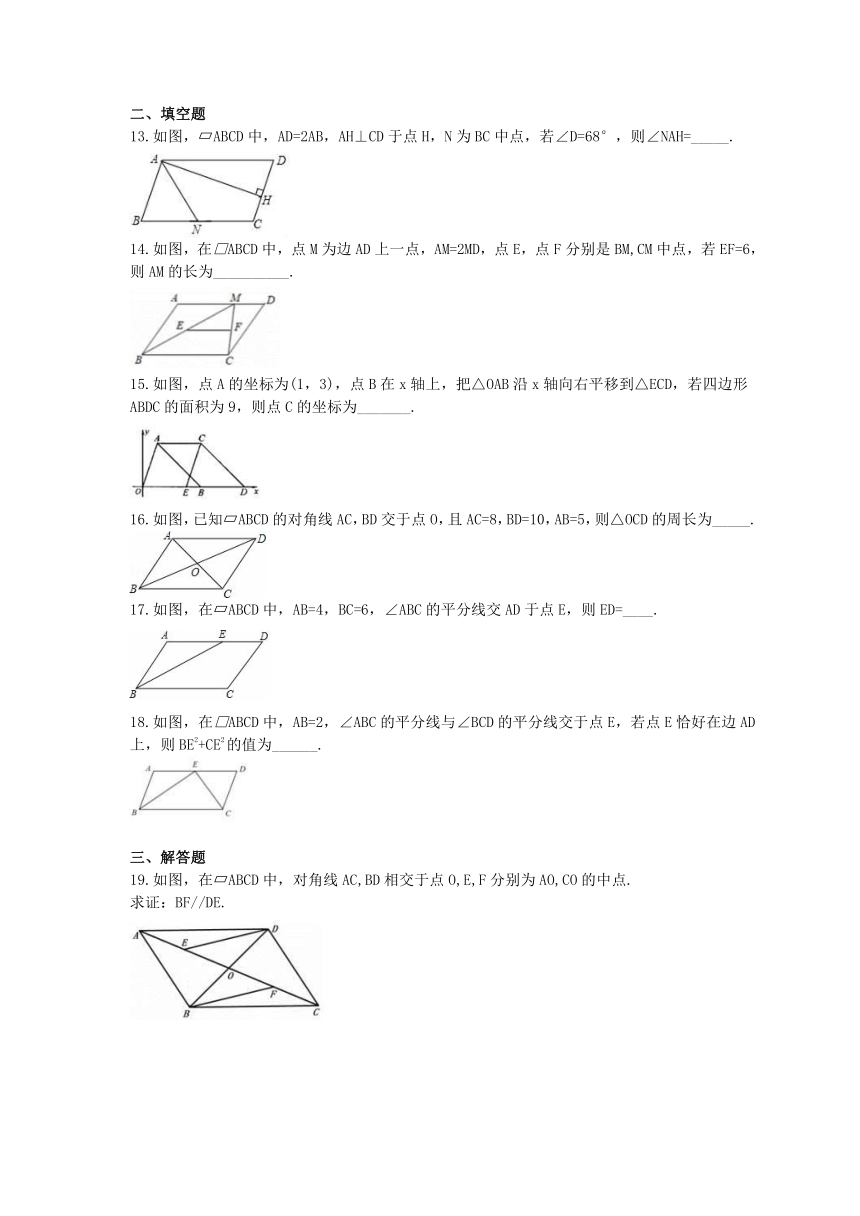
13.如图,?ABCD中,AD=2AB,AH⊥CD于点H,N为BC中点,若∠D=68°,则∠NAH=_____.
14.如图,在□ABCD中,点M为边AD上一点,AM=2MD,点E,点F分别是BM,CM中点,若EF=6,则AM的长为__________.
15.如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移到△ECD,若四边形ABDC的面积为9,则点C的坐标为_______.
16.如图,已知?ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为_____.
17.如图,在?ABCD中,AB=4,BC=6,∠ABC的平分线交AD于点E,则ED=____.
18.如图,在□ABCD中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为______.
三 、解答题
19.如图,在?ABCD中,对角线AC,BD相交于点O,E,F分别为AO,CO的中点.
求证:BF//DE.
20.如图,在?ABCD中,点E,F分别AD,BC在上,且AE=CF,EF,BD相交于点O.
求证:OE=OF.
21.如图,,在平行四边ABCD中,点E是BC上的一点,连接DE,在DE上取一点F使得∠AFE=∠ADC.若DE = AD,求证:DF = CE.
22.如图,F为?ABCD的边BC的延长线上的一点,且CF=BC,连接AF交CD于点E,对角线AC,BD相交于点O,连接OE.求证:CF=2OE.
23.如图,平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点M、N,若△CON的面积为2,△DOM的面积为4,求△AOB的面积.
24.已知在□ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2.
(1)若CF=2,AE=3,求BE的长;
(2)求证:2∠CEG=∠AGE.
参考答案
1.答案为:C
2.答案为:A
3.答案为:B.
4.答案为:C
5.答案为:B
6.答案为:C
7.答案为:B??? ?
8.答案为:A
9.答案为:A
10.答案为:B
11.答案为:B?
12.答案为:C
13.答案为:34°.
14.答案为:8.
15.答案为:(4,3).
16.答案为:14
17.答案为:2.
18.答案为:16.
19.解:连接DF、BE,如图:
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵E,F分别为AO,CO的中点,
∴EO=FO,
∴四边形DEBF为平行四边形,
∴BF∥DE.
20.证明:作业帮连接BE、DF,如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OF=OE.
21.证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠ADF=∠DEC,
∵∠AFE=∠FAD+∠ADF,∠ADC=∠ADF+∠CDE,∠AFE=∠ADC,
∴∠FAD=∠CDE,
在△AFD和△DCE中,,
∴△AFD≌△DCE,
∴DF=CE.
22.证明:如图,连接DF.
∵四边形ABCD是平行四边形,F为?ABCD的边BC的延长线上的一点,
∴点O是AC的中点,AD∥BC,且AD=BC,
又∵CF=BC,
∴AD∥CF,AD=CF,
∴四边形ACFD是平行四边形,
∴点E是CD的中点,
∴OE是△ACF的中位线,
∴CF=2OE.
23.解:∵四边形ABCD是平行四边形,
∴∠CAD=∠ACB,OA=OC,
而∠AOM=∠NOC,
∴△CON≌△AOM(ASA).
∴S△AOD=4+2=6.
又∵OB=OD,
∴S△AOB=S△AOD=6.
24.解:(1)∵点F为CE的中点,
∴CE=CD=2CF=4.
又∵四边形ABCD为平行四边形,
∴AB=CD=4.
在Rt△ABE中,由勾股定理得BE=.
(2)证明:延长AG、BC交于点H.
∵CE=CD,∠1=∠2,∠ECG=∠DCF,
∴△CEG≌△CDF(AAS).
∴CG=CF.
∵CD=CE=2CF,
∴CG=GD.
∵AD∥BC,
∴∠DAG=∠CHG,∠ADG=∠HCG.
∴△ADG≌△HCG(AAS).
∴AG=HG.
∵∠AEH=90°,
∴EG=AG=HG.
∴∠CEG=∠H.
∵∠AGE=∠CEG+∠H,
∴∠AGE=2∠CEG.
即2∠CEG=∠AGE.
一、选择题
1.下列命题中,是真命题的是(??? )
A.平行四边形的对角线一定相等
B.等腰三角形任意一条边上的高线、中线和角平分线都三线合一
C.三角形的中位线平行于第三边并且等于它的一半
D.三角形的两边之和小于第三边
2.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2??? B.1:3??? C.1:4??? D.1:5
3.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E, 且AE=3,则AB的长为(? )
A.4???? ??? B.3 ??? ??? C.2.5??? ??? D.2???
4.如图,在?ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5????? B.6????? C.4????? D.5
5.如图,将?ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为( )
A.102°????? B.112°????? C.122°????? D.92°
6.已知平行四边形的一边长为14,下列各组数据中能分别作为它的两条对角线的长的是( )
A.10与16 ??B.12与16??? ???C.20与22 ????D.10与40
7.如图,A、B两点被一座山隔开,M、N分别是AC、BC中点,测量MN的长度为40m,那么AB的长度为( )
A.40m??? B.80m???? C.160m????? D.不能确定
8.平行四边形ABCD与等边三角形AEF按如图所示的方式摆放,如果∠B=45°,则∠BAE的大小是( )
A.75°?? ??B.80°??? ?C.100°? ???D.120°
9.如图,四边形ABCD是平行四边形,点A、B、C的坐标分别为(2,0)、(0,1)、(1,2),则AB+BC的值为( )
A.???? B.3?????? C.4?????? D.5
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC=14,则EF的长是 (??? )
A.2??????????? B.3????????? C.4??????????? D.5
11.如图所示,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3,则AC的长是( )
A.12???? B.14????? C.16???? D.18
12.如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,2AB=BC,连接OE.
下列结论:①∠CAD=30°;②S?ABCD=AB·AC;③OB=AB;④4OE=BC.成立的个数有( ? ?)
A.1个?? ? B.2个??? C.3个? ? D.4个
二 、填空题
13.如图,?ABCD中,AD=2AB,AH⊥CD于点H,N为BC中点,若∠D=68°,则∠NAH=_____.
14.如图,在□ABCD中,点M为边AD上一点,AM=2MD,点E,点F分别是BM,CM中点,若EF=6,则AM的长为__________.
15.如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移到△ECD,若四边形ABDC的面积为9,则点C的坐标为_______.
16.如图,已知?ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为_____.
17.如图,在?ABCD中,AB=4,BC=6,∠ABC的平分线交AD于点E,则ED=____.
18.如图,在□ABCD中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为______.
三 、解答题
19.如图,在?ABCD中,对角线AC,BD相交于点O,E,F分别为AO,CO的中点.
求证:BF//DE.
20.如图,在?ABCD中,点E,F分别AD,BC在上,且AE=CF,EF,BD相交于点O.
求证:OE=OF.
21.如图,,在平行四边ABCD中,点E是BC上的一点,连接DE,在DE上取一点F使得∠AFE=∠ADC.若DE = AD,求证:DF = CE.
22.如图,F为?ABCD的边BC的延长线上的一点,且CF=BC,连接AF交CD于点E,对角线AC,BD相交于点O,连接OE.求证:CF=2OE.
23.如图,平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点M、N,若△CON的面积为2,△DOM的面积为4,求△AOB的面积.
24.已知在□ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2.
(1)若CF=2,AE=3,求BE的长;
(2)求证:2∠CEG=∠AGE.
参考答案
1.答案为:C
2.答案为:A
3.答案为:B.
4.答案为:C
5.答案为:B
6.答案为:C
7.答案为:B??? ?
8.答案为:A
9.答案为:A
10.答案为:B
11.答案为:B?
12.答案为:C
13.答案为:34°.
14.答案为:8.
15.答案为:(4,3).
16.答案为:14
17.答案为:2.
18.答案为:16.
19.解:连接DF、BE,如图:
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵E,F分别为AO,CO的中点,
∴EO=FO,
∴四边形DEBF为平行四边形,
∴BF∥DE.
20.证明:作业帮连接BE、DF,如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OF=OE.
21.证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠ADF=∠DEC,
∵∠AFE=∠FAD+∠ADF,∠ADC=∠ADF+∠CDE,∠AFE=∠ADC,
∴∠FAD=∠CDE,
在△AFD和△DCE中,,
∴△AFD≌△DCE,
∴DF=CE.
22.证明:如图,连接DF.
∵四边形ABCD是平行四边形,F为?ABCD的边BC的延长线上的一点,
∴点O是AC的中点,AD∥BC,且AD=BC,
又∵CF=BC,
∴AD∥CF,AD=CF,
∴四边形ACFD是平行四边形,
∴点E是CD的中点,
∴OE是△ACF的中位线,
∴CF=2OE.
23.解:∵四边形ABCD是平行四边形,
∴∠CAD=∠ACB,OA=OC,
而∠AOM=∠NOC,
∴△CON≌△AOM(ASA).
∴S△AOD=4+2=6.
又∵OB=OD,
∴S△AOB=S△AOD=6.
24.解:(1)∵点F为CE的中点,
∴CE=CD=2CF=4.
又∵四边形ABCD为平行四边形,
∴AB=CD=4.
在Rt△ABE中,由勾股定理得BE=.
(2)证明:延长AG、BC交于点H.
∵CE=CD,∠1=∠2,∠ECG=∠DCF,
∴△CEG≌△CDF(AAS).
∴CG=CF.
∵CD=CE=2CF,
∴CG=GD.
∵AD∥BC,
∴∠DAG=∠CHG,∠ADG=∠HCG.
∴△ADG≌△HCG(AAS).
∴AG=HG.
∵∠AEH=90°,
∴EG=AG=HG.
∴∠CEG=∠H.
∵∠AGE=∠CEG+∠H,
∴∠AGE=2∠CEG.
即2∠CEG=∠AGE.
