人教版数学八年级下册17.1勾股定理精选练习 (Word版含答案)
文档属性
| 名称 | 人教版数学八年级下册17.1勾股定理精选练习 (Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览


文档简介
17.1《勾股定理》精选练习
一、选择题
1.以下列各组数为边长,能组成直角三角形的是(??? )
A.2,3,4?? B.10,8,4? C.7,25,24?? D.7,15,12
2.已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90○,则(??? )
A.b2= a2+ c2 ;?? B.c2= a2+ b2;?? C.a2+b2=c2;?? D.a+b=c
3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25?? ?? B.14?? ?? C.7?? ? D.7或25
4.如图,直角三角形ABC的周长为24,且AB:BC=5:3,则AC= (?? )
A.6?? ? B.8??? ? C.10??? D.12
5.如图,线段AB=、CD=,那么,线段EF的长度为( )
A.????? B.????? C.???? D.
6.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( )
A.8????? B.4?????? C.6????? D.无法计算
7.一只蚂蚁沿直角三角形的边长爬行一周需2秒,如果将直角三角形的边长扩大1倍,那么这只蚂蚁再沿边长爬行一周需(?? ).
A.6秒??? B.5秒???? C.4秒??? D.3秒
8.已知一直角三角形的木板,三边的平方和为12800cm2,则斜边长为( )
A.80cm?????? B.30cm????? C.90cm?????? D.120cm
9.一架2.5米长的梯子,斜立在一竖直的墙上,这时梯子的底端离墙0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯子底端在水平方向上滑动( ? )
A.0.9米??? B.0.8米??? C.0.5米??? D.0.4米
10.小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,则旗杆的高是(? ).
A.8米?? ? B.10米? ? C.12米?? ? D.14米
11.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于(?? )
A.10? ?????? B.7??? ???C.5? ????? D.4
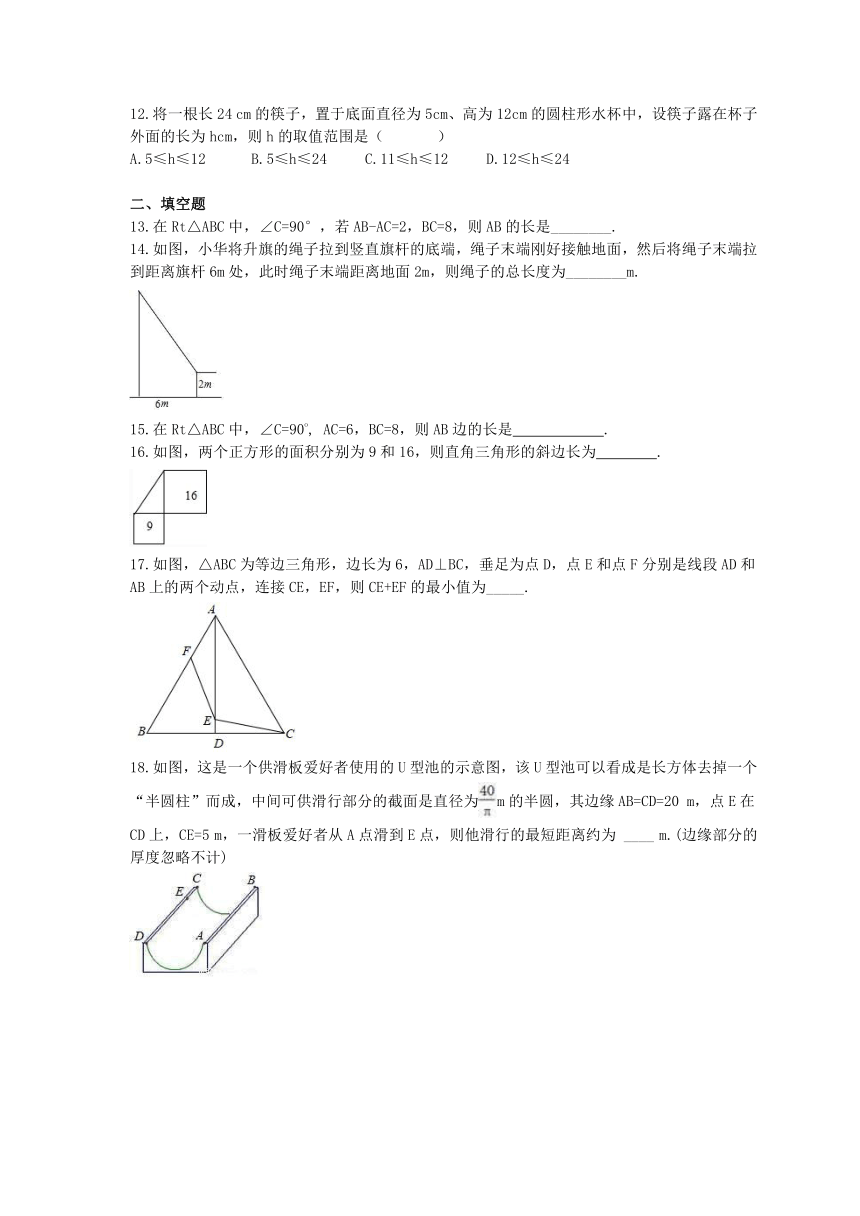
12.将一根长24 cm的筷子,置于底面直径为5cm、高为12cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是(??? )
A.5≤h≤12 ??B.5≤h≤24 C.11≤h≤12? D.12≤h≤24
二 、填空题
13.在Rt△ABC中,∠C=90°,若AB-AC=2,BC=8,则AB的长是________.
14.如图,小华将升旗的绳子拉到竖直旗杆的底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆6m处,此时绳子末端距离地面2m,则绳子的总长度为________m.
15.在Rt△ABC中,∠C=90o, AC=6,BC=8,则AB边的长是 .
16.如图,两个正方形的面积分别为9和16,则直角三角形的斜边长为 .
17.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为_____.
18.如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=5 m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 ____ m.(边缘部分的厚度忽略不计)
三、作图题
19.已知一个三角形的三边长分别为和.
(1)请在右边网格中画出此三角形并使三个顶点均落在格点上;
(2)该三角形的面积是________.
四、解答题
20.如图,在7×7网格中,每个小正方形边长都为1.建立适当的平面直角坐标系,使点A(3,4)、C(4,2).
(1)判断△ABC的形状,并求图中格点△ABC的面积;
(2)在x轴上有一点P,使得PA+PC最小,则PA+PC的最小值为__________.
21.如图,AF⊥DE于F,且DF=15 cm,EF=6 cm,AE=10 cm.求正方形ABCD的面积.
22.如图,台风过后,一希望小学的旗杆在某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,你能求出旗杆在离底部多少米的位置断裂吗?
23.已知Rt△ABC中,其中两边的长分别是3,5,求第三边的长.
24.如图,已知AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分面积.
?
参考答案
1.答案为:C
2.答案为:A
3.答案为:C
4.答案为:B?
5.答案为:C.
6.答案为:A.
7.答案为:C
8.答案为:A.
9.答案为:B
10.答案为:C
11.答案为:C
12.答案为:C;
13.答案为:17.
14.答案为:10
15.答案为:10
16.答案为:5
17.答案为:3.
18.答案为:25
19.解:(1)如图所示,即为所求;
(2)12.
20.解:(1)如图,建立直角坐标系,
∴B的坐标是(0,0).
∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,BC=,AC=
∴S△ABC=BC×AC=××=5;
(2)如图所示:作点C关于x轴的对称点C′连接AC′交x轴与点P,连接PC.
∵点C与点C′关于x轴对称,
∴PC=PC′.
∴AP+PC=AP+PC.
∴当A,P,C′在一条直线上时,AP+PC有最小值,最小值为AC′的长.
∵AC′=.∴AP+PC的最小值为.故答案为:.
21.解:在Rt△AEF中,AF2=AE2-EF2=64,
在Rt△AFD中,AD2=AF2+DF2=289,
所以正方形ABCD的面积是289 cm2
22.解:如图,过点A作AD⊥BC于点D.
在Rt△ABD中,由勾股定理得AD2=AB2-BD2.
在Rt△ACD中,由勾股定理得AD2=AC2-CD2.
所以AB2-BD2=AC2-CD2.
设BD=x,则82-x2=62-(7-x)2,解得x=5.5,即BD=5.5.
所以AD≈5.8.
所以S△ABC=0.5·BC·AD≈0.5×7×5.8=20.3≈20.
23.解:当已知两条边是直角边时,由勾股定理得第三条边的长为=;
当已知两条边中有一条是直角边而另一条是斜边时,第三边长为=4.
∴第三边的长为或4.
24.解:在Rt△ACD中,AC=5;
在Rt△ACD中,BC=12;
∴S△ABC=0.5×5×12=30,
S△ACD=0.5×4×3=6,
∴阴影部分面积为30﹣6=24.
一、选择题
1.以下列各组数为边长,能组成直角三角形的是(??? )
A.2,3,4?? B.10,8,4? C.7,25,24?? D.7,15,12
2.已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90○,则(??? )
A.b2= a2+ c2 ;?? B.c2= a2+ b2;?? C.a2+b2=c2;?? D.a+b=c
3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25?? ?? B.14?? ?? C.7?? ? D.7或25
4.如图,直角三角形ABC的周长为24,且AB:BC=5:3,则AC= (?? )
A.6?? ? B.8??? ? C.10??? D.12
5.如图,线段AB=、CD=,那么,线段EF的长度为( )
A.????? B.????? C.???? D.
6.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( )
A.8????? B.4?????? C.6????? D.无法计算
7.一只蚂蚁沿直角三角形的边长爬行一周需2秒,如果将直角三角形的边长扩大1倍,那么这只蚂蚁再沿边长爬行一周需(?? ).
A.6秒??? B.5秒???? C.4秒??? D.3秒
8.已知一直角三角形的木板,三边的平方和为12800cm2,则斜边长为( )
A.80cm?????? B.30cm????? C.90cm?????? D.120cm
9.一架2.5米长的梯子,斜立在一竖直的墙上,这时梯子的底端离墙0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯子底端在水平方向上滑动( ? )
A.0.9米??? B.0.8米??? C.0.5米??? D.0.4米
10.小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,则旗杆的高是(? ).
A.8米?? ? B.10米? ? C.12米?? ? D.14米
11.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于(?? )
A.10? ?????? B.7??? ???C.5? ????? D.4
12.将一根长24 cm的筷子,置于底面直径为5cm、高为12cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是(??? )
A.5≤h≤12 ??B.5≤h≤24 C.11≤h≤12? D.12≤h≤24
二 、填空题
13.在Rt△ABC中,∠C=90°,若AB-AC=2,BC=8,则AB的长是________.
14.如图,小华将升旗的绳子拉到竖直旗杆的底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆6m处,此时绳子末端距离地面2m,则绳子的总长度为________m.
15.在Rt△ABC中,∠C=90o, AC=6,BC=8,则AB边的长是 .
16.如图,两个正方形的面积分别为9和16,则直角三角形的斜边长为 .
17.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为_____.
18.如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=5 m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 ____ m.(边缘部分的厚度忽略不计)
三、作图题
19.已知一个三角形的三边长分别为和.
(1)请在右边网格中画出此三角形并使三个顶点均落在格点上;
(2)该三角形的面积是________.
四、解答题
20.如图,在7×7网格中,每个小正方形边长都为1.建立适当的平面直角坐标系,使点A(3,4)、C(4,2).
(1)判断△ABC的形状,并求图中格点△ABC的面积;
(2)在x轴上有一点P,使得PA+PC最小,则PA+PC的最小值为__________.
21.如图,AF⊥DE于F,且DF=15 cm,EF=6 cm,AE=10 cm.求正方形ABCD的面积.
22.如图,台风过后,一希望小学的旗杆在某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,你能求出旗杆在离底部多少米的位置断裂吗?
23.已知Rt△ABC中,其中两边的长分别是3,5,求第三边的长.
24.如图,已知AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分面积.
?
参考答案
1.答案为:C
2.答案为:A
3.答案为:C
4.答案为:B?
5.答案为:C.
6.答案为:A.
7.答案为:C
8.答案为:A.
9.答案为:B
10.答案为:C
11.答案为:C
12.答案为:C;
13.答案为:17.
14.答案为:10
15.答案为:10
16.答案为:5
17.答案为:3.
18.答案为:25
19.解:(1)如图所示,即为所求;
(2)12.
20.解:(1)如图,建立直角坐标系,
∴B的坐标是(0,0).
∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,BC=,AC=
∴S△ABC=BC×AC=××=5;
(2)如图所示:作点C关于x轴的对称点C′连接AC′交x轴与点P,连接PC.
∵点C与点C′关于x轴对称,
∴PC=PC′.
∴AP+PC=AP+PC.
∴当A,P,C′在一条直线上时,AP+PC有最小值,最小值为AC′的长.
∵AC′=.∴AP+PC的最小值为.故答案为:.
21.解:在Rt△AEF中,AF2=AE2-EF2=64,
在Rt△AFD中,AD2=AF2+DF2=289,
所以正方形ABCD的面积是289 cm2
22.解:如图,过点A作AD⊥BC于点D.
在Rt△ABD中,由勾股定理得AD2=AB2-BD2.
在Rt△ACD中,由勾股定理得AD2=AC2-CD2.
所以AB2-BD2=AC2-CD2.
设BD=x,则82-x2=62-(7-x)2,解得x=5.5,即BD=5.5.
所以AD≈5.8.
所以S△ABC=0.5·BC·AD≈0.5×7×5.8=20.3≈20.
23.解:当已知两条边是直角边时,由勾股定理得第三条边的长为=;
当已知两条边中有一条是直角边而另一条是斜边时,第三边长为=4.
∴第三边的长为或4.
24.解:在Rt△ACD中,AC=5;
在Rt△ACD中,BC=12;
∴S△ABC=0.5×5×12=30,
S△ACD=0.5×4×3=6,
∴阴影部分面积为30﹣6=24.
