28.2.1解直角三角形-人教版九年级数学下册20分钟课后精华同步轻松练(Word版 含解析)
文档属性
| 名称 | 28.2.1解直角三角形-人教版九年级数学下册20分钟课后精华同步轻松练(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 177.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 08:08:10 | ||
图片预览



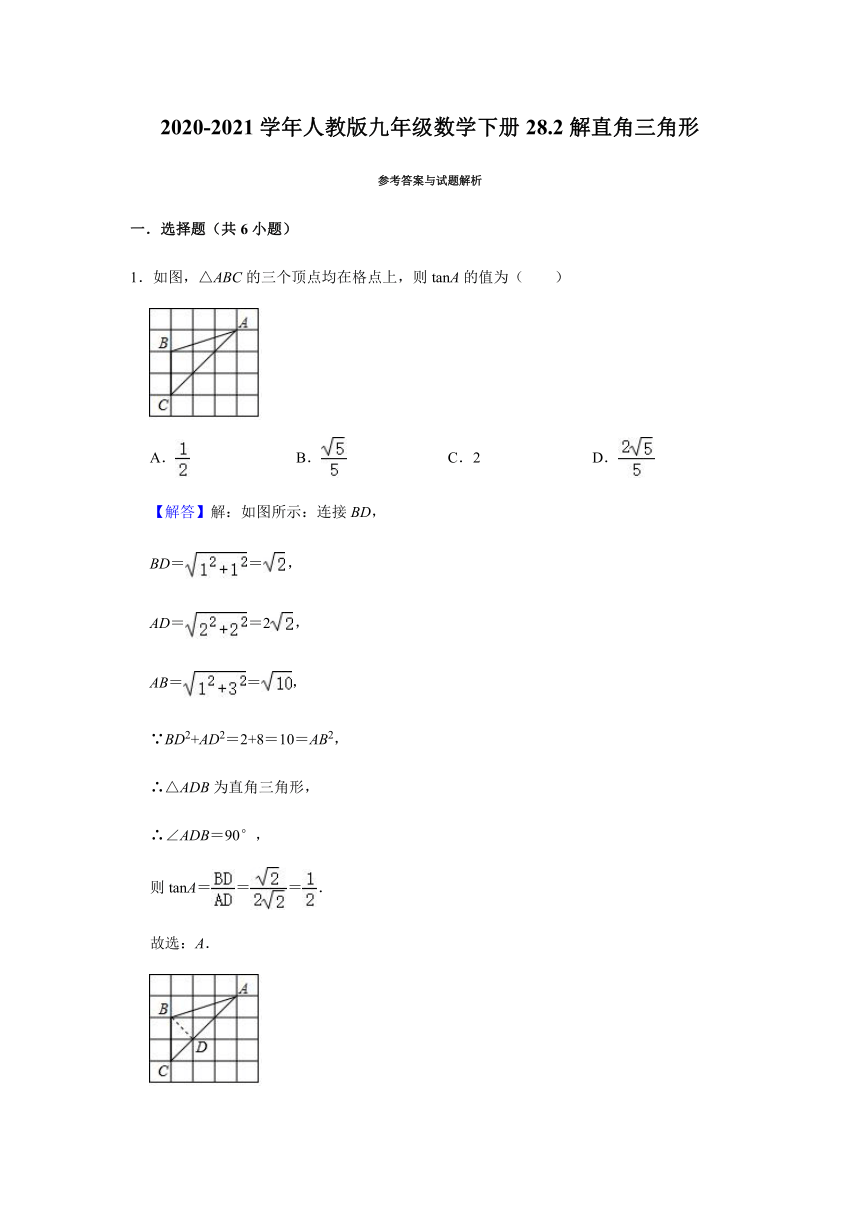
文档简介
2020-2021学年人教版九年级数学下册28.2解直角三角形
一.选择题(共6小题)
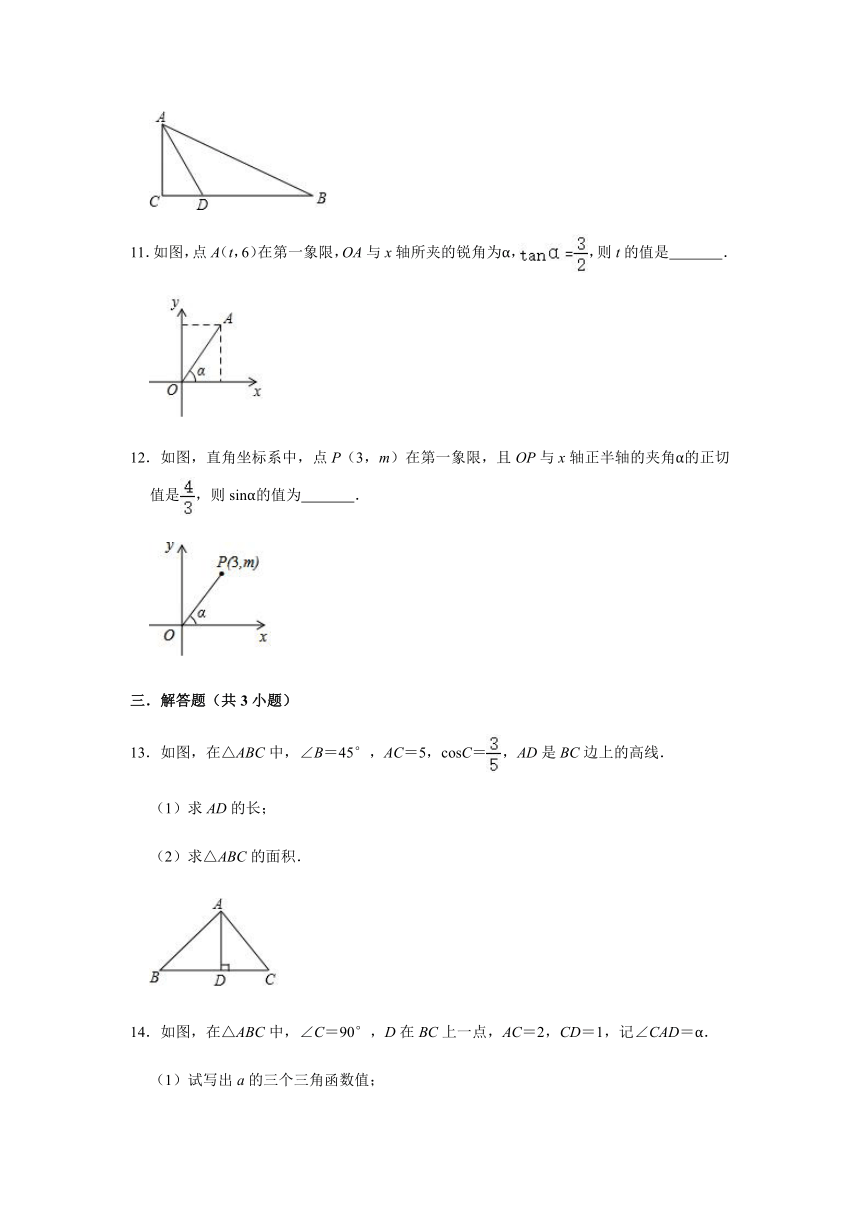
1.如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.2
D.
2.在△ABC中,∠A=40°,∠C=90°,BC=7,则AB边的长是( )
A.7sin40°
B.7cos40°
C.
D.
3.如图,在△ABC中,AC=1,BC=2,AB=,则sinB的值是( )
A.
B.
C.2
D.
4.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
A.
B.
C.
D.
5.如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A.
B.
C.
D.
6.在Rt△ABC中,∠C=90°,AB=10,sin∠B=,则BC=( )
A.15
B.6
C.9
D.8
二.填空题(共6小题)
7.三角形在正方形网格纸中的位置如图所示,则sinα的值是
.
8.在△ABC中,AB=10,AC=8,B为锐角且,则BC=
.
9.如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=,BC=12,则AD的长
.
10.在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,,则AC的长是
.
11.如图,点A(t,6)在第一象限,OA与x轴所夹的锐角为α,,则t的值是
.
12.如图,直角坐标系中,点P(3,m)在第一象限,且OP与x轴正半轴的夹角α的正切值是,则sinα的值为
.
三.解答题(共3小题)
13.如图,在△ABC中,∠B=45°,AC=5,cosC=,AD是BC边上的高线.
(1)求AD的长;
(2)求△ABC的面积.
14.如图,在△ABC中,∠C=90°,D在BC上一点,AC=2,CD=1,记∠CAD=α.
(1)试写出a的三个三角函数值;
(2)若∠B=α,求BD的长.
15.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且sinα=,AB=4,求AD的长.
2020-2021学年人教版九年级数学下册28.2解直角三角形
参考答案与试题解析
一.选择题(共6小题)
1.如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.2
D.
【解答】解:如图所示:连接BD,
BD==,
AD==2,
AB==,
∵BD2+AD2=2+8=10=AB2,
∴△ADB为直角三角形,
∴∠ADB=90°,
则tanA===.
故选:A.
2.在△ABC中,∠A=40°,∠C=90°,BC=7,则AB边的长是( )
A.7sin40°
B.7cos40°
C.
D.
【解答】解:∵在△ABC中,∠A=40°,∠C=90°,BC=7,
∴sinA=,
∴AB==.
故选:C.
3.如图,在△ABC中,AC=1,BC=2,AB=,则sinB的值是( )
A.
B.
C.2
D.
【解答】解:∵在△ABC中,∠ACB=90°,AC=1,BC=2,AB=,
∴sinB=.
故选:B.
4.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
A.
B.
C.
D.
【解答】解:过点C作CD⊥AB于点D,
∵AD=3,CD=4,
∴由勾股定理可知:AC=5,
∴cos∠BAC==,
故选:C.
5.如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A.
B.
C.
D.
【解答】解:如图,作AH⊥CB,交CB延长线于H点,
tan∠ACB=.
故选:A.
6.在Rt△ABC中,∠C=90°,AB=10,sin∠B=,则BC=( )
A.15
B.6
C.9
D.8
【解答】解:∵sinB==,
∴AC=AB×=6,
∴直角△ABC中,BC===8.
故选:D.
二.填空题(共6小题)
7.三角形在正方形网格纸中的位置如图所示,则sinα的值是 .
【解答】解:如图所示:∵AC=3,BC=4,
∴AB=5,
∴sinα==.
故答案为:.
8.在△ABC中,AB=10,AC=8,B为锐角且,则BC= 8+2或8﹣2 .
【解答】解:过点A作AD⊥BC,垂足为D,
①当∠ACB为锐角时,如图1,
在Rt△ABD中,BD=AB?cosB=10×=8,
AD==6,
在Rt△ACD中,CD==2,
∴BC=BD+CD=8+2,
②当∠ACB为钝角时,如图2,
在Rt△ABD中,BD=AB?cosB=10×=8,
AD==6,
在Rt△ACD中,CD==2,
∴BC=BD﹣CD=8﹣2,
故答案为:8+2或8﹣2.
9.如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=,BC=12,则AD的长 8 .
【解答】解:在Rt△ADC中,sinC==,
设AD=12x,则AC=13x,
∴DC==5x,
∵cos∠DAC=sinC=,
∴tanB=,
在Rt△ABD中,∵tanB==,
而AD=12x,
∴BD=13x,
∴13x+5x=12,解得x=,
∴AD=12x=8.
故答案为8.
10.在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,,则AC的长是 .
【解答】解:设CD=x,则AC==x,
∵AC2+BC2=AB2,AC2+(CD+BD)2=AB2,
∴(
x)2+(x+2)2=(2
)2,
解得,x=1,∴AC=.
故答案为.
11.如图,点A(t,6)在第一象限,OA与x轴所夹的锐角为α,,则t的值是 4 .
【解答】解:如图,
∵A(t,6),且在第一象限,
∴OB=t,AB=6,
在Rt△AOB中,
∵tanα==,即=,
∴t=4,
故答案为:4.
12.如图,直角坐标系中,点P(3,m)在第一象限,且OP与x轴正半轴的夹角α的正切值是,则sinα的值为 .
【解答】解:过点P作PA⊥x轴于点A,
∴OA=3,PA=m,
∵tanα=,
∴=,
∴m=4,
由勾股定理可知:OP=5,
∴sinα==,
故答案为:
三.解答题(共3小题)
13.如图,在△ABC中,∠B=45°,AC=5,cosC=,AD是BC边上的高线.
(1)求AD的长;
(2)求△ABC的面积.
【解答】解:(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°.
在Rt△ACD中,AC=5,cosC=,
∴CD=AC?cosC=3,
∴AD==4.
(2)∵∠B=45°,∠ADB=90°,
∴∠BAD=90°﹣∠B=45°,
∴∠B=∠BAD,
∴BD=AD=4,
∴S△ABC=AD?BC=×4×(4+3)=14.
14.如图,在△ABC中,∠C=90°,D在BC上一点,AC=2,CD=1,记∠CAD=α.
(1)试写出a的三个三角函数值;
(2)若∠B=α,求BD的长.
【解答】解:(1)在Rt△ACD中,AC=2,CD=1,
根据勾股定理得:AD==,
则sinα==,cosα==,tanα=;
(2)∵∠CAD=∠B=α,∠C=∠C=90°,
∴△ACD∽△BCA,
设BD=x,则BC=x+1,
∴=,即=,
解得:x=3,
则BD=3.
15.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且sinα=,AB=4,求AD的长.
【解答】解:∵四边形ABCD为矩形,
∴AD=BC,∠BAD=90°,
∵DE⊥AC,
∴∠ADE+∠DAE=90°,
而∠BAC+∠DAE=90°,
∴∠BAC=∠ADE=α,
在Rt△ABC中,∵sin∠BAC=,
∴=,
设BC=4x,则AC=5x,
∴AB=3x,
∴3x=4,解得x=,
∴BC=
∴AD=.
一.选择题(共6小题)
1.如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.2
D.
2.在△ABC中,∠A=40°,∠C=90°,BC=7,则AB边的长是( )
A.7sin40°
B.7cos40°
C.
D.
3.如图,在△ABC中,AC=1,BC=2,AB=,则sinB的值是( )
A.
B.
C.2
D.
4.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
A.
B.
C.
D.
5.如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A.
B.
C.
D.
6.在Rt△ABC中,∠C=90°,AB=10,sin∠B=,则BC=( )
A.15
B.6
C.9
D.8
二.填空题(共6小题)
7.三角形在正方形网格纸中的位置如图所示,则sinα的值是
.
8.在△ABC中,AB=10,AC=8,B为锐角且,则BC=
.
9.如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=,BC=12,则AD的长
.
10.在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,,则AC的长是
.
11.如图,点A(t,6)在第一象限,OA与x轴所夹的锐角为α,,则t的值是
.
12.如图,直角坐标系中,点P(3,m)在第一象限,且OP与x轴正半轴的夹角α的正切值是,则sinα的值为
.
三.解答题(共3小题)
13.如图,在△ABC中,∠B=45°,AC=5,cosC=,AD是BC边上的高线.
(1)求AD的长;
(2)求△ABC的面积.
14.如图,在△ABC中,∠C=90°,D在BC上一点,AC=2,CD=1,记∠CAD=α.
(1)试写出a的三个三角函数值;
(2)若∠B=α,求BD的长.
15.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且sinα=,AB=4,求AD的长.
2020-2021学年人教版九年级数学下册28.2解直角三角形
参考答案与试题解析
一.选择题(共6小题)
1.如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.2
D.
【解答】解:如图所示:连接BD,
BD==,
AD==2,
AB==,
∵BD2+AD2=2+8=10=AB2,
∴△ADB为直角三角形,
∴∠ADB=90°,
则tanA===.
故选:A.
2.在△ABC中,∠A=40°,∠C=90°,BC=7,则AB边的长是( )
A.7sin40°
B.7cos40°
C.
D.
【解答】解:∵在△ABC中,∠A=40°,∠C=90°,BC=7,
∴sinA=,
∴AB==.
故选:C.
3.如图,在△ABC中,AC=1,BC=2,AB=,则sinB的值是( )
A.
B.
C.2
D.
【解答】解:∵在△ABC中,∠ACB=90°,AC=1,BC=2,AB=,
∴sinB=.
故选:B.
4.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
A.
B.
C.
D.
【解答】解:过点C作CD⊥AB于点D,
∵AD=3,CD=4,
∴由勾股定理可知:AC=5,
∴cos∠BAC==,
故选:C.
5.如图,在8×4的正方形网格中,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
A.
B.
C.
D.
【解答】解:如图,作AH⊥CB,交CB延长线于H点,
tan∠ACB=.
故选:A.
6.在Rt△ABC中,∠C=90°,AB=10,sin∠B=,则BC=( )
A.15
B.6
C.9
D.8
【解答】解:∵sinB==,
∴AC=AB×=6,
∴直角△ABC中,BC===8.
故选:D.
二.填空题(共6小题)
7.三角形在正方形网格纸中的位置如图所示,则sinα的值是 .
【解答】解:如图所示:∵AC=3,BC=4,
∴AB=5,
∴sinα==.
故答案为:.
8.在△ABC中,AB=10,AC=8,B为锐角且,则BC= 8+2或8﹣2 .
【解答】解:过点A作AD⊥BC,垂足为D,
①当∠ACB为锐角时,如图1,
在Rt△ABD中,BD=AB?cosB=10×=8,
AD==6,
在Rt△ACD中,CD==2,
∴BC=BD+CD=8+2,
②当∠ACB为钝角时,如图2,
在Rt△ABD中,BD=AB?cosB=10×=8,
AD==6,
在Rt△ACD中,CD==2,
∴BC=BD﹣CD=8﹣2,
故答案为:8+2或8﹣2.
9.如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC,若sinC=,BC=12,则AD的长 8 .
【解答】解:在Rt△ADC中,sinC==,
设AD=12x,则AC=13x,
∴DC==5x,
∵cos∠DAC=sinC=,
∴tanB=,
在Rt△ABD中,∵tanB==,
而AD=12x,
∴BD=13x,
∴13x+5x=12,解得x=,
∴AD=12x=8.
故答案为8.
10.在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,,则AC的长是 .
【解答】解:设CD=x,则AC==x,
∵AC2+BC2=AB2,AC2+(CD+BD)2=AB2,
∴(
x)2+(x+2)2=(2
)2,
解得,x=1,∴AC=.
故答案为.
11.如图,点A(t,6)在第一象限,OA与x轴所夹的锐角为α,,则t的值是 4 .
【解答】解:如图,
∵A(t,6),且在第一象限,
∴OB=t,AB=6,
在Rt△AOB中,
∵tanα==,即=,
∴t=4,
故答案为:4.
12.如图,直角坐标系中,点P(3,m)在第一象限,且OP与x轴正半轴的夹角α的正切值是,则sinα的值为 .
【解答】解:过点P作PA⊥x轴于点A,
∴OA=3,PA=m,
∵tanα=,
∴=,
∴m=4,
由勾股定理可知:OP=5,
∴sinα==,
故答案为:
三.解答题(共3小题)
13.如图,在△ABC中,∠B=45°,AC=5,cosC=,AD是BC边上的高线.
(1)求AD的长;
(2)求△ABC的面积.
【解答】解:(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°.
在Rt△ACD中,AC=5,cosC=,
∴CD=AC?cosC=3,
∴AD==4.
(2)∵∠B=45°,∠ADB=90°,
∴∠BAD=90°﹣∠B=45°,
∴∠B=∠BAD,
∴BD=AD=4,
∴S△ABC=AD?BC=×4×(4+3)=14.
14.如图,在△ABC中,∠C=90°,D在BC上一点,AC=2,CD=1,记∠CAD=α.
(1)试写出a的三个三角函数值;
(2)若∠B=α,求BD的长.
【解答】解:(1)在Rt△ACD中,AC=2,CD=1,
根据勾股定理得:AD==,
则sinα==,cosα==,tanα=;
(2)∵∠CAD=∠B=α,∠C=∠C=90°,
∴△ACD∽△BCA,
设BD=x,则BC=x+1,
∴=,即=,
解得:x=3,
则BD=3.
15.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且sinα=,AB=4,求AD的长.
【解答】解:∵四边形ABCD为矩形,
∴AD=BC,∠BAD=90°,
∵DE⊥AC,
∴∠ADE+∠DAE=90°,
而∠BAC+∠DAE=90°,
∴∠BAC=∠ADE=α,
在Rt△ABC中,∵sin∠BAC=,
∴=,
设BC=4x,则AC=5x,
∴AB=3x,
∴3x=4,解得x=,
∴BC=
∴AD=.
