28.2.2应用举例-人教版九年级数学下册20分钟课后精华同步轻松练(Word版 含解析)
文档属性
| 名称 | 28.2.2应用举例-人教版九年级数学下册20分钟课后精华同步轻松练(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 221.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 08:12:05 | ||
图片预览



文档简介
2020-2021学年人教版九年级数学下册28.2.2应用举例
一.选择题(共6小题)
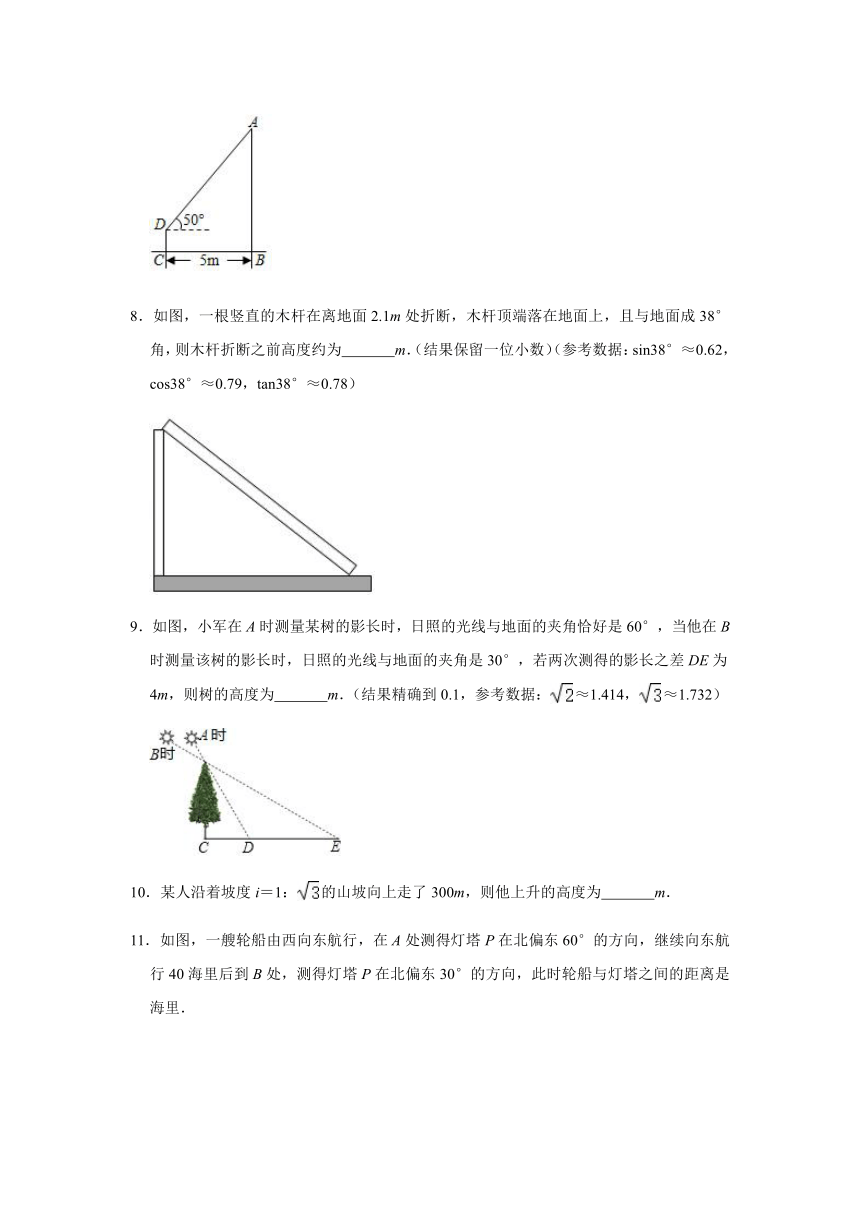
1.如图,某河堤迎水坡AB的坡比i=tan∠CAB=1:,堤高BC=5m,则坡面AB的长是( )
A.5
m
B.10m
C.5m
D.8
m
2.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
3.从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米
B.14米
C.21米
D.42米
4.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( )(参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.32)
A.12千米
B.(3+4)千米
C.(3+5)千米
D.(12﹣4)千米
5.如图,在高2m,坡角为30°的楼梯表面铺地毯地毯的长度至少需要( )
A.2m
B.(2+2)m
C.4m
D.(4+2)m
6.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200米
C.220米
D.米
二.填空题(共6小题)
7.如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为
m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
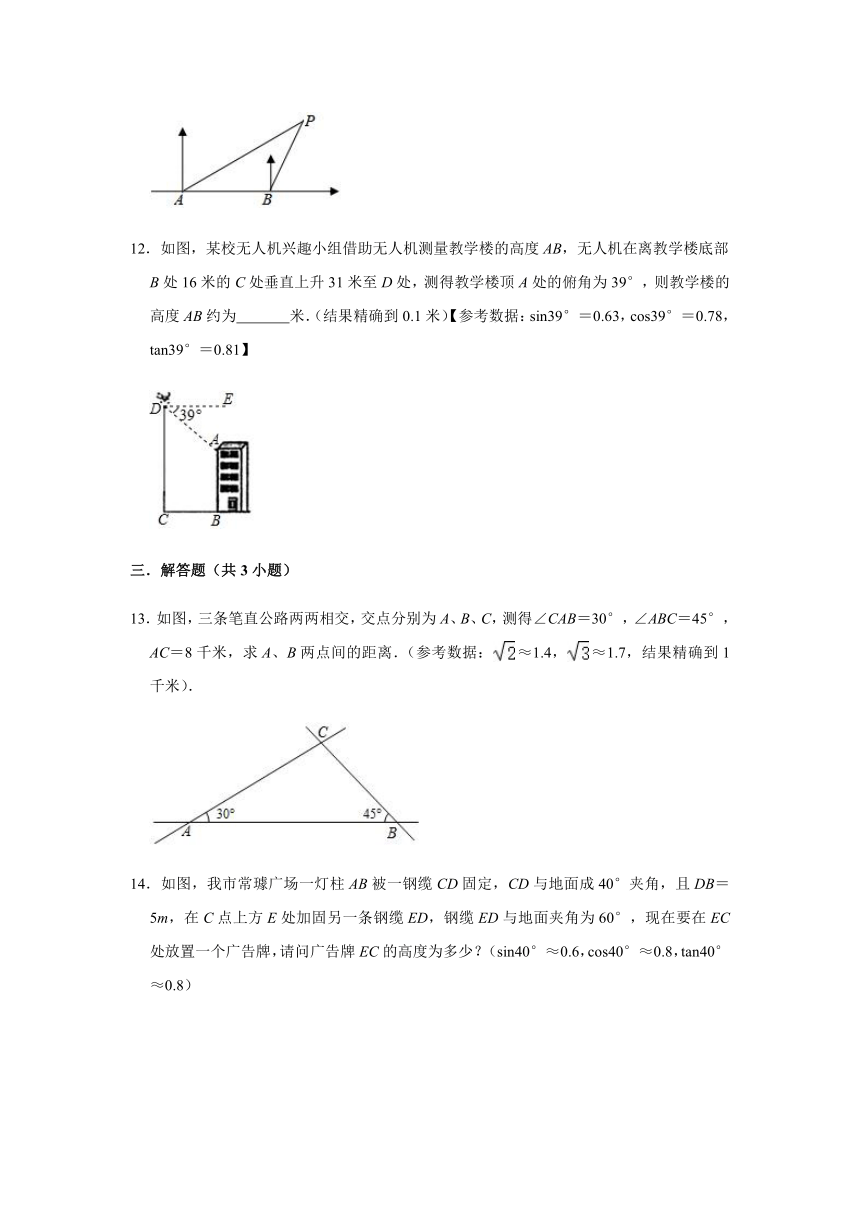
8.如图,一根竖直的木杆在离地面2.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为
m.(结果保留一位小数)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
9.如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60°,当他在B时测量该树的影长时,日照的光线与地面的夹角是30°,若两次测得的影长之差DE为4m,则树的高度为
m.(结果精确到0.1,参考数据:≈1.414,≈1.732)
10.某人沿着坡度i=1:的山坡向上走了300m,则他上升的高度为
m.
11.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是
海里.
12.如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,则教学楼的高度AB约为
米.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】
三.解答题(共3小题)
13.如图,三条笔直公路两两相交,交点分别为A、B、C,测得∠CAB=30°,∠ABC=45°,AC=8千米,求A、B两点间的距离.(参考数据:≈1.4,≈1.7,结果精确到1千米).
14.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
15.浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
2020-2021学年人教版九年级数学下册28.2.2应用举例
参考答案与试题解析
一.选择题(共6小题)
1.如图,某河堤迎水坡AB的坡比i=tan∠CAB=1:,堤高BC=5m,则坡面AB的长是( )
A.5
m
B.10m
C.5m
D.8
m
【解答】解:∵tan∠CAB===,
∴在Rt△ABC中,∠BAC=30°,
又∵BC=5m,
∴AB=2BC=10m,
故选:B.
2.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
【解答】解:在Rt△ABC中,sinB=,
∴AC=AB?sinB=10sin36°,
故选:C.
3.从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米
B.14米
C.21米
D.42米
【解答】解:根据题意可得:船离海岸线的距离为42÷tan30°=42(米)
故选:A.
4.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( )(参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.32)
A.12千米
B.(3+4)千米
C.(3+5)千米
D.(12﹣4)千米
【解答】解:如图,作BD⊥AC于点D,
根据题意可知:
在Rt△ADB中,∠A=60°,AB=6千米,
∴AD=3千米,BD=3千米,
在Rt△CDB中,∠CBD=53°,
∴CD=BD?tan53°≈3×1.32≈3×≈4(千米),
∴AC=AD+CD=3+4(千米).
则A,C两地的距离为(3+4)千米.
故选:B.
5.如图,在高2m,坡角为30°的楼梯表面铺地毯地毯的长度至少需要( )
A.2m
B.(2+2)m
C.4m
D.(4+2)m
【解答】解:如图,
由题意得:地毯的竖直的线段加起来等于BC,水平的线段相加正好等于AC,
即地毯的总长度至少为(AC+BC),
在Rt△ABC中,∠A=30°,BC=2m,∠C=90°.
∵tanA=,
∴AC=BC÷tan30°=2.
∴AC+BC=2+2.
故选:B.
6.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200米
C.220米
D.米
【解答】解:∵在热气球C处测得地面B点的俯角为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
二.填空题(共6小题)
7.如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为 7.5 m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
【解答】解:如图,过点D作DE⊥AB,垂足为点E,则DE=BC=5,DC=BE=1.5,
在Rt△ADE中,
∵tan∠ADE=,
∴AE=tan∠ADE?DE=tan50°×5≈1.19×5=5.95(米),
∴AB=AE+BE=5.95+1.5≈7.5(米),
故答案为:7.5.
8.如图,一根竖直的木杆在离地面2.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 5.5 m.(结果保留一位小数)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
【解答】解:由题意可知:BC=2.1,∠A=38°,
∴sin38°=,
∴AB=≈3.4,
∴AB+BC≈3.4+2.1=5.5,
故答案为:5.5
9.如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60°,当他在B时测量该树的影长时,日照的光线与地面的夹角是30°,若两次测得的影长之差DE为4m,则树的高度为 3.5 m.(结果精确到0.1,参考数据:≈1.414,≈1.732)
【解答】解:如图所示,由题意可得:∠CDF=60°,∠E=30°,∠FCD=90°,
则设DC=x,故tan60°===,
则FC=x,
∵tan30°===,
∴EC=3x,
∴DE=EC﹣DC=3x﹣x=2x=4,
解得:x=2,
则EC=x=2≈3.5(m).
故答案为:3.5.
10.某人沿着坡度i=1:的山坡向上走了300m,则他上升的高度为 150 m.
【解答】解:如图所示.
∵BC:AB=1:.
∴∠A=30°.
∵AC=300m,
∴BC=300×sin30°=150(m).
故答案为:150.
11.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是 40 海里.
【解答】解:如图所示:由题意可得,∠PAB=30°,∠DBP=30°,
故∠PBE=60°,
则∠P=∠PAB=30°,
可得:AB=BP=40海里.
故答案为:40.
12.如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,则教学楼的高度AB约为 18.0 米.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】
【解答】解:过点A作AM⊥CD于点M,则∠DAM=∠ADE=39°,如图所示.
在Rt△ADM中,AM=16,∠DAM=39°,
∴DM=AM?tan∠DAM=16×0.81=12.96,
∴AB=CM=CD﹣DM=31﹣12.96=18.04≈18.0.
故答案为:18.0.
三.解答题(共3小题)
13.如图,三条笔直公路两两相交,交点分别为A、B、C,测得∠CAB=30°,∠ABC=45°,AC=8千米,求A、B两点间的距离.(参考数据:≈1.4,≈1.7,结果精确到1千米).
【解答】解:过点C作CD⊥AB于点D,如图所示.
在Rt△ACD中,AC=8(千米),∠CAD=30°,∠CDA=90°,
∴CD=AC?sin∠CAD=4(千米),AD=AC?cos∠CAD=4(千米)≈6.8(千米).
在Rt△BCD中,CD=4(千米),∠BDC=90°,∠CBD=45°,
∴∠BCD=45°,
∴BD=CD=4(千米),
∴AB=AD+BD=6.8+4≈11(千米).
答:A、B两点间的距离约为11千米.
14.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
【解答】解:在Rt△CDB中,tan∠BDC=,
∴BC=BDtan40°≈4,
在Rt△BDE中,tan∠BDE=,
∴BE=BDtan∠BDE=5,
∴CE=BE﹣BC≈4.66(m),
答:广告牌EC的高度约为4.66m.
15.浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
【解答】解:过点B作CD⊥AC于点D,
∵∠A=30°,AB=60,
∴BD=AB=30,
∴AD=BD=30,
在Rt△CBD中,
tan49°=,sin49°=,
∴CD≈26,BC≈40,
∴AC=AD+CD≈78.
一.选择题(共6小题)
1.如图,某河堤迎水坡AB的坡比i=tan∠CAB=1:,堤高BC=5m,则坡面AB的长是( )
A.5
m
B.10m
C.5m
D.8
m
2.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
3.从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米
B.14米
C.21米
D.42米
4.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( )(参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.32)
A.12千米
B.(3+4)千米
C.(3+5)千米
D.(12﹣4)千米
5.如图,在高2m,坡角为30°的楼梯表面铺地毯地毯的长度至少需要( )
A.2m
B.(2+2)m
C.4m
D.(4+2)m
6.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200米
C.220米
D.米
二.填空题(共6小题)
7.如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为
m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
8.如图,一根竖直的木杆在离地面2.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为
m.(结果保留一位小数)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
9.如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60°,当他在B时测量该树的影长时,日照的光线与地面的夹角是30°,若两次测得的影长之差DE为4m,则树的高度为
m.(结果精确到0.1,参考数据:≈1.414,≈1.732)
10.某人沿着坡度i=1:的山坡向上走了300m,则他上升的高度为
m.
11.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是
海里.
12.如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,则教学楼的高度AB约为
米.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】
三.解答题(共3小题)
13.如图,三条笔直公路两两相交,交点分别为A、B、C,测得∠CAB=30°,∠ABC=45°,AC=8千米,求A、B两点间的距离.(参考数据:≈1.4,≈1.7,结果精确到1千米).
14.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
15.浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
2020-2021学年人教版九年级数学下册28.2.2应用举例
参考答案与试题解析
一.选择题(共6小题)
1.如图,某河堤迎水坡AB的坡比i=tan∠CAB=1:,堤高BC=5m,则坡面AB的长是( )
A.5
m
B.10m
C.5m
D.8
m
【解答】解:∵tan∠CAB===,
∴在Rt△ABC中,∠BAC=30°,
又∵BC=5m,
∴AB=2BC=10m,
故选:B.
2.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
【解答】解:在Rt△ABC中,sinB=,
∴AC=AB?sinB=10sin36°,
故选:C.
3.从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42米
B.14米
C.21米
D.42米
【解答】解:根据题意可得:船离海岸线的距离为42÷tan30°=42(米)
故选:A.
4.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( )(参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.32)
A.12千米
B.(3+4)千米
C.(3+5)千米
D.(12﹣4)千米
【解答】解:如图,作BD⊥AC于点D,
根据题意可知:
在Rt△ADB中,∠A=60°,AB=6千米,
∴AD=3千米,BD=3千米,
在Rt△CDB中,∠CBD=53°,
∴CD=BD?tan53°≈3×1.32≈3×≈4(千米),
∴AC=AD+CD=3+4(千米).
则A,C两地的距离为(3+4)千米.
故选:B.
5.如图,在高2m,坡角为30°的楼梯表面铺地毯地毯的长度至少需要( )
A.2m
B.(2+2)m
C.4m
D.(4+2)m
【解答】解:如图,
由题意得:地毯的竖直的线段加起来等于BC,水平的线段相加正好等于AC,
即地毯的总长度至少为(AC+BC),
在Rt△ABC中,∠A=30°,BC=2m,∠C=90°.
∵tanA=,
∴AC=BC÷tan30°=2.
∴AC+BC=2+2.
故选:B.
6.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200米
C.220米
D.米
【解答】解:∵在热气球C处测得地面B点的俯角为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
二.填空题(共6小题)
7.如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为 7.5 m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
【解答】解:如图,过点D作DE⊥AB,垂足为点E,则DE=BC=5,DC=BE=1.5,
在Rt△ADE中,
∵tan∠ADE=,
∴AE=tan∠ADE?DE=tan50°×5≈1.19×5=5.95(米),
∴AB=AE+BE=5.95+1.5≈7.5(米),
故答案为:7.5.
8.如图,一根竖直的木杆在离地面2.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为 5.5 m.(结果保留一位小数)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
【解答】解:由题意可知:BC=2.1,∠A=38°,
∴sin38°=,
∴AB=≈3.4,
∴AB+BC≈3.4+2.1=5.5,
故答案为:5.5
9.如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60°,当他在B时测量该树的影长时,日照的光线与地面的夹角是30°,若两次测得的影长之差DE为4m,则树的高度为 3.5 m.(结果精确到0.1,参考数据:≈1.414,≈1.732)
【解答】解:如图所示,由题意可得:∠CDF=60°,∠E=30°,∠FCD=90°,
则设DC=x,故tan60°===,
则FC=x,
∵tan30°===,
∴EC=3x,
∴DE=EC﹣DC=3x﹣x=2x=4,
解得:x=2,
则EC=x=2≈3.5(m).
故答案为:3.5.
10.某人沿着坡度i=1:的山坡向上走了300m,则他上升的高度为 150 m.
【解答】解:如图所示.
∵BC:AB=1:.
∴∠A=30°.
∵AC=300m,
∴BC=300×sin30°=150(m).
故答案为:150.
11.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是 40 海里.
【解答】解:如图所示:由题意可得,∠PAB=30°,∠DBP=30°,
故∠PBE=60°,
则∠P=∠PAB=30°,
可得:AB=BP=40海里.
故答案为:40.
12.如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,则教学楼的高度AB约为 18.0 米.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】
【解答】解:过点A作AM⊥CD于点M,则∠DAM=∠ADE=39°,如图所示.
在Rt△ADM中,AM=16,∠DAM=39°,
∴DM=AM?tan∠DAM=16×0.81=12.96,
∴AB=CM=CD﹣DM=31﹣12.96=18.04≈18.0.
故答案为:18.0.
三.解答题(共3小题)
13.如图,三条笔直公路两两相交,交点分别为A、B、C,测得∠CAB=30°,∠ABC=45°,AC=8千米,求A、B两点间的距离.(参考数据:≈1.4,≈1.7,结果精确到1千米).
【解答】解:过点C作CD⊥AB于点D,如图所示.
在Rt△ACD中,AC=8(千米),∠CAD=30°,∠CDA=90°,
∴CD=AC?sin∠CAD=4(千米),AD=AC?cos∠CAD=4(千米)≈6.8(千米).
在Rt△BCD中,CD=4(千米),∠BDC=90°,∠CBD=45°,
∴∠BCD=45°,
∴BD=CD=4(千米),
∴AB=AD+BD=6.8+4≈11(千米).
答:A、B两点间的距离约为11千米.
14.如图,我市常璩广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,在C点上方E处加固另一条钢缆ED,钢缆ED与地面夹角为60°,现在要在EC处放置一个广告牌,请问广告牌EC的高度为多少?(sin40°≈0.6,cos40°≈0.8,tan40°≈0.8)
【解答】解:在Rt△CDB中,tan∠BDC=,
∴BC=BDtan40°≈4,
在Rt△BDE中,tan∠BDE=,
∴BE=BDtan∠BDE=5,
∴CE=BE﹣BC≈4.66(m),
答:广告牌EC的高度约为4.66m.
15.浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
【解答】解:过点B作CD⊥AC于点D,
∵∠A=30°,AB=60,
∴BD=AB=30,
∴AD=BD=30,
在Rt△CBD中,
tan49°=,sin49°=,
∴CD≈26,BC≈40,
∴AC=AD+CD≈78.
