苏科版八年级数学上册期末复习第3章勾股定理 题型专项训练-(word版含答案)
文档属性
| 名称 | 苏科版八年级数学上册期末复习第3章勾股定理 题型专项训练-(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览

文档简介
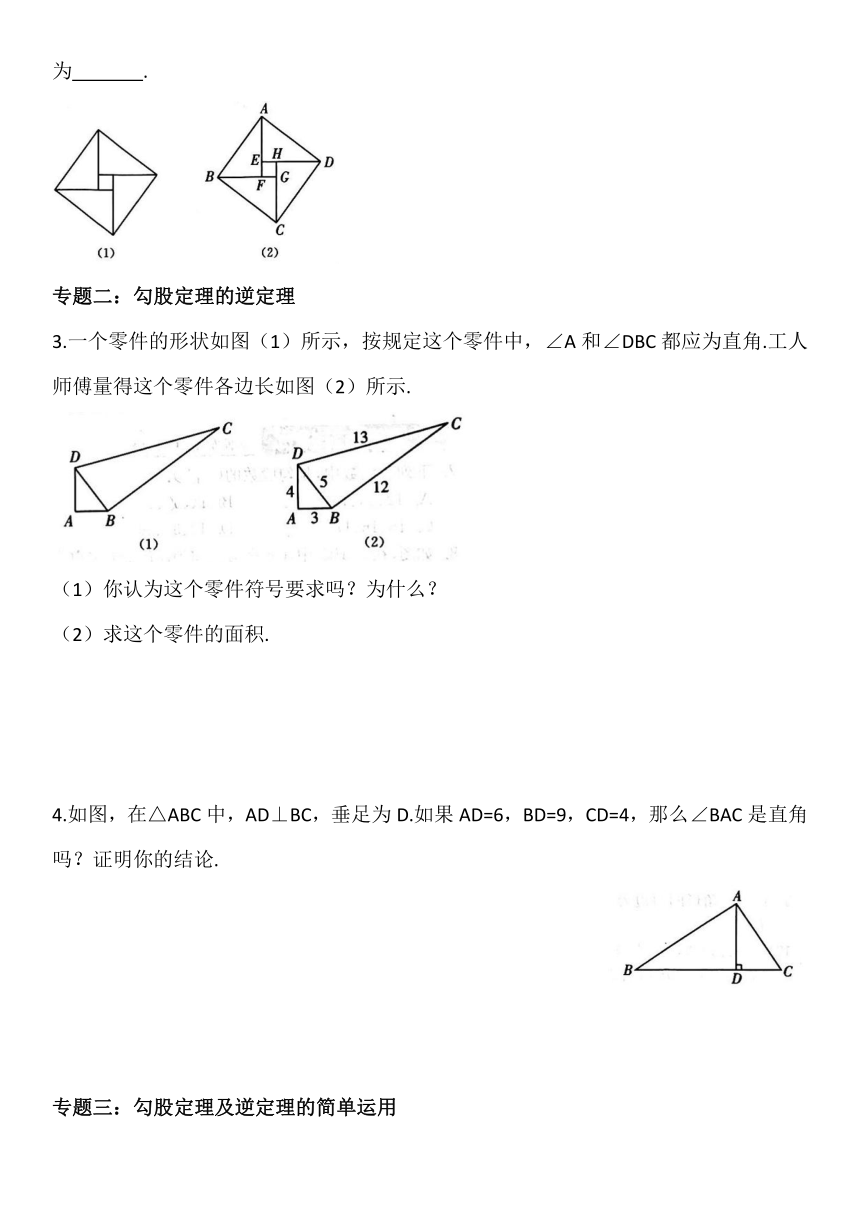
苏科版八年级上册期末复习训练3:勾股定理
知识导图
专题一:勾股定理及其证明
1.如图,以直角三角形为边,向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足图形个数有(
)
2.如图(1),这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图(2),其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为
.
专题二:勾股定理的逆定理
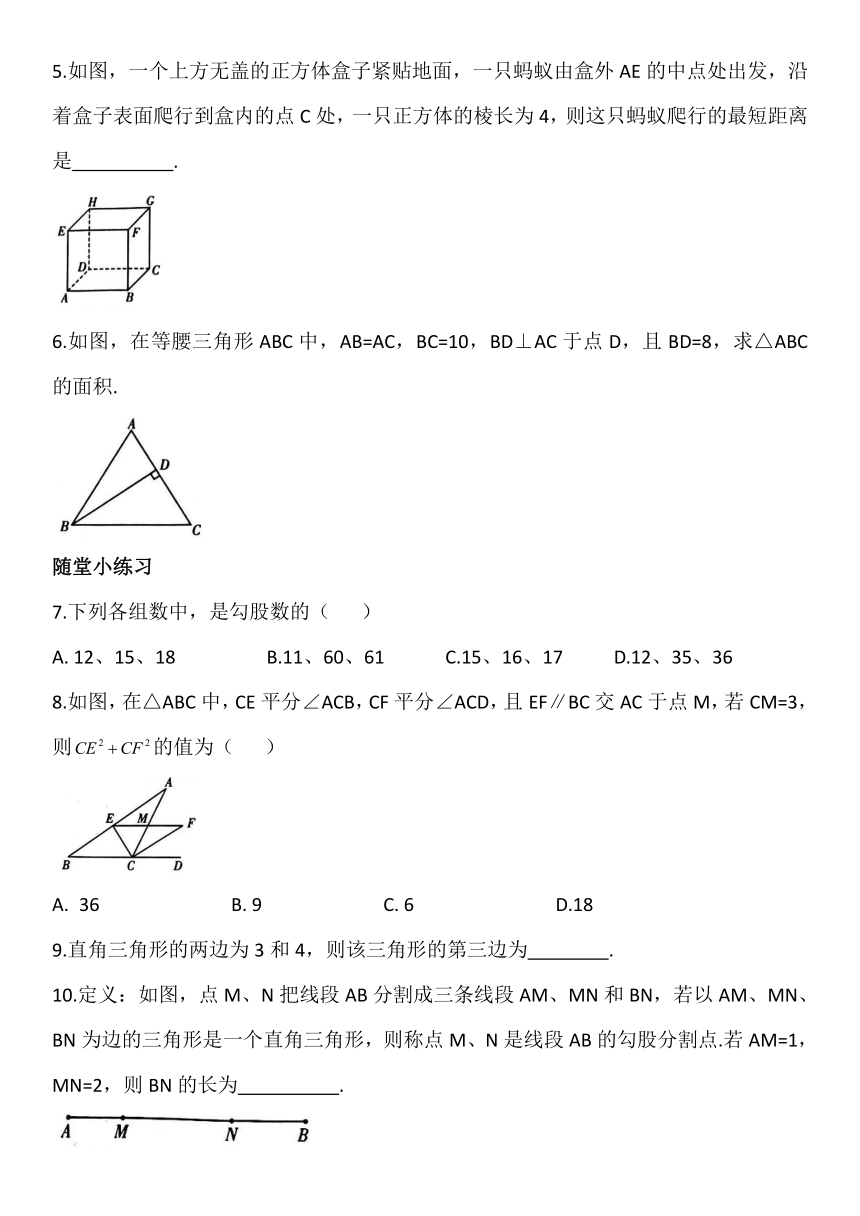
3.一个零件的形状如图(1)所示,按规定这个零件中,∠A和∠DBC都应为直角.工人师傅量得这个零件各边长如图(2)所示.
你认为这个零件符号要求吗?为什么?
求这个零件的面积.
4.如图,在△ABC中,AD⊥BC,垂足为D.如果AD=6,BD=9,CD=4,那么∠BAC是直角吗?证明你的结论.
专题三:勾股定理及逆定理的简单运用
5.如图,一个上方无盖的正方体盒子紧贴地面,一只蚂蚁由盒外AE的中点处出发,沿着盒子表面爬行到盒内的点C处,一只正方体的棱长为4,则这只蚂蚁爬行的最短距离是
.
6.如图,在等腰三角形ABC中,AB=AC,BC=10,BD⊥AC于点D,且BD=8,求△ABC的面积.
随堂小练习
7.下列各组数中,是勾股数的(
)
A.
12、15、18
B.11、60、61
C.15、16、17
D.12、35、36
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M,若CM=3,则的值为(
)
36
B.
9
C.
6
D.18
9.直角三角形的两边为3和4,则该三角形的第三边为
.
10.定义:如图,点M、N把线段AB分割成三条线段AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.若AM=1,MN=2,则BN的长为
.
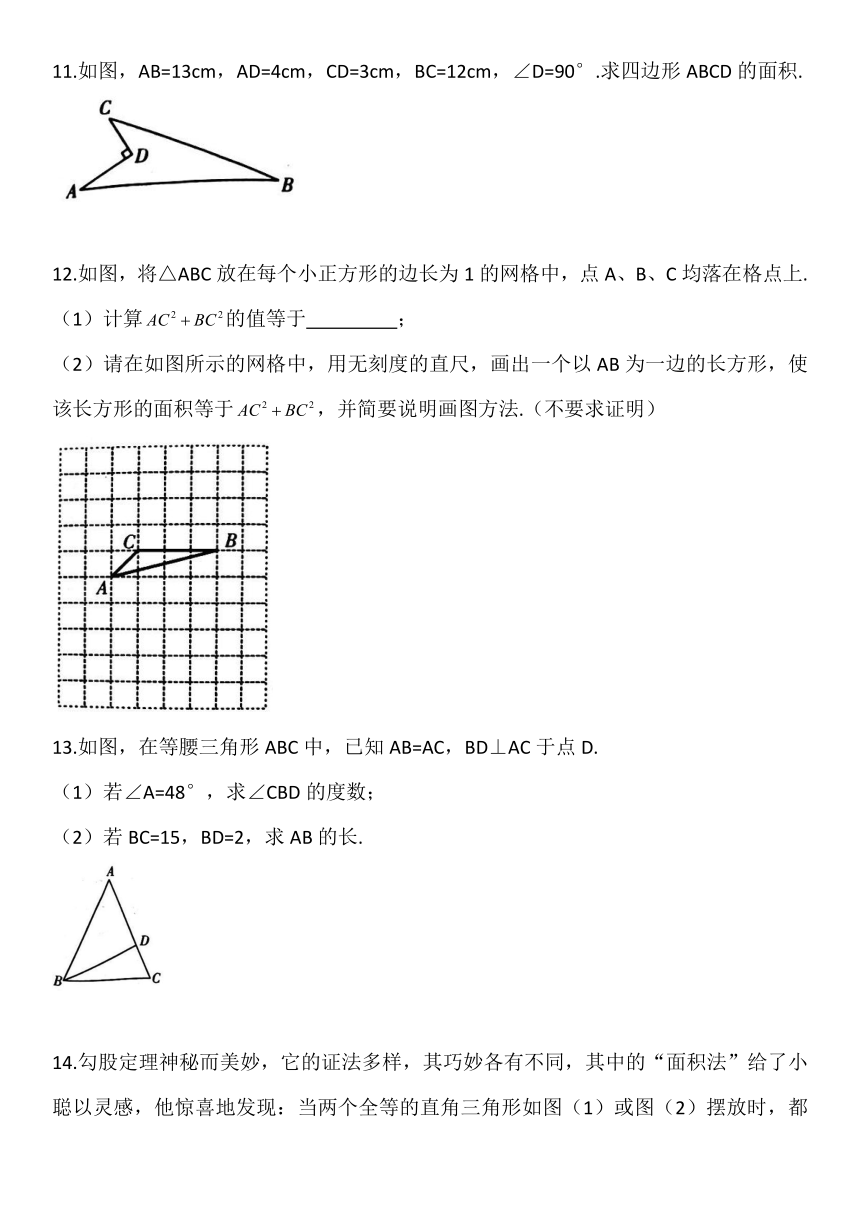
11.如图,AB=13cm,AD=4cm,CD=3cm,BC=12cm,∠D=90°.求四边形ABCD的面积.
12.如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
(1)计算的值等于
;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的长方形,使该长方形的面积等于,并简要说明画图方法.(不要求证明)
13.如图,在等腰三角形ABC中,已知AB=AC,BD⊥AC于点D.
(1)若∠A=48°,求∠CBD的度数;
(2)若BC=15,BD=2,求AB的长.
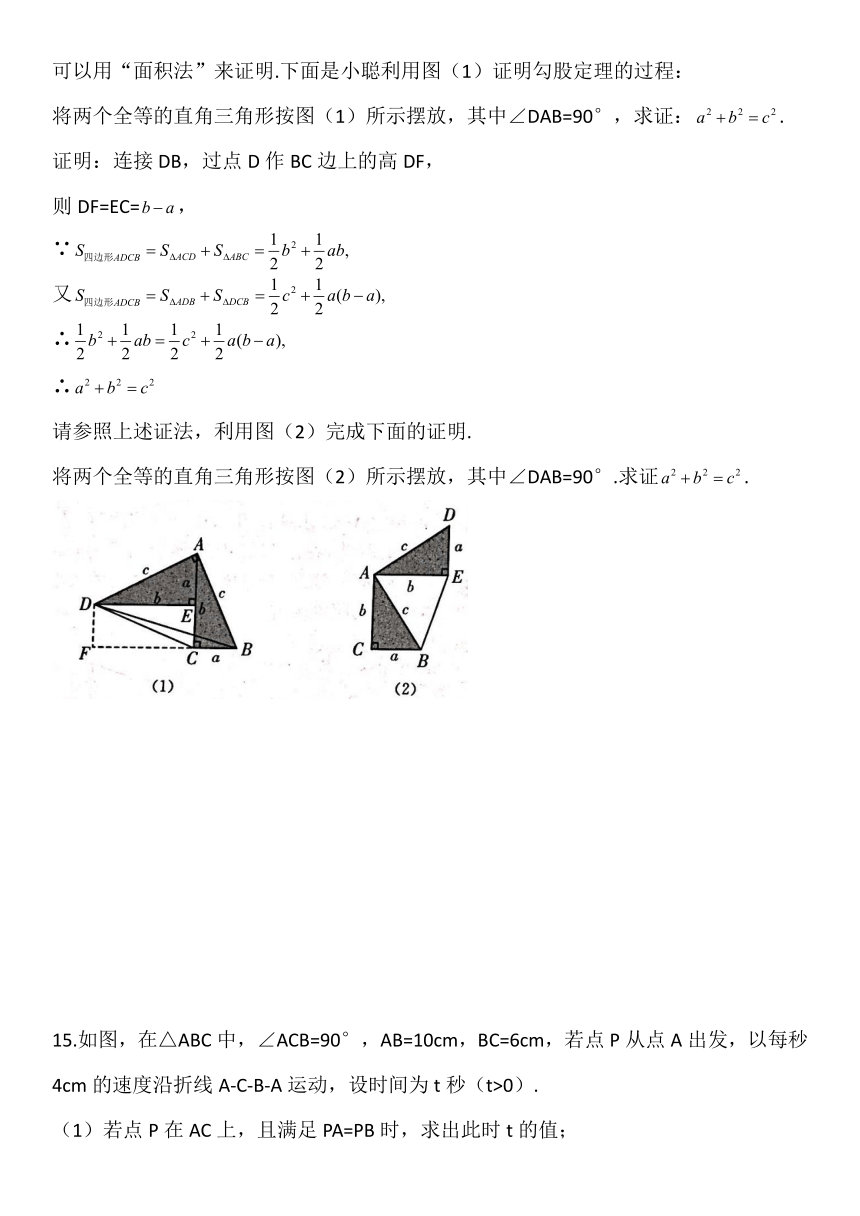
14.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现:当两个全等的直角三角形如图(1)或图(2)摆放时,都可以用“面积法”来证明.下面是小聪利用图(1)证明勾股定理的过程:
将两个全等的直角三角形按图(1)所示摆放,其中∠DAB=90°,求证:.
证明:连接DB,过点D作BC边上的高DF,
则DF=EC=,
∵
又
∴
∴
请参照上述证法,利用图(2)完成下面的证明.
将两个全等的直角三角形按图(2)所示摆放,其中∠DAB=90°.求证.
15.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A-C-B-A运动,设时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,当△BCP为等腰三角形时,请直接写出t的值.
专项提优特训:
类型一:利用勾股定理解决平面图形的折叠问题
1.如图,将长方形ABCD沿EF折叠,使顶点C恰好在AB边的中点C′上,若AB=6,BC=9,则BF的长为(
).
4
B.
C.4.5
D.
5
2.如图,在长方形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在C′处,BC′交AD于点E,则线段DE的长为(
).
A.
3
B.
C.
5
D.
3.为了向建国七十一周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班里开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作的第一、二个步骤是:
①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD;
②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处.
请你根据①②步骤解答下列问题:计算EC、FC的长.
类型二:利用勾股定理解决立体图形的展开问题
4.如图,圆柱的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是(
).
6cm
B.
12cm
C.
13cm
D.
16cm
5.如图,圆柱形玻璃杯高为12cm,底边周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为
cm.
6.一位同学要用彩带装饰一个长方体礼盒.长方体高6cm,底面是边长为4cm的正方形,从顶点A到顶点C′如何贴彩带用的彩带最短?最短长度是多少?
7.如图,一个长方体形状的木柜在墙角处(与墙面和底面均没有缝隙),有一只蚂蚁从柜脚A处沿着木柜表面爬到柜脚处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,=5时,求蚂蚁爬过的最短路径的长.
参考答案
D
10
(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB?+AD?=BD?,BD?+BC?=DC?,
∴△ABD、△BDC都是直角三角形.
∴∠A=90°,∠DBC=90°.
故这个零件符合要求.
(2)这个零件的面积为
故这个零件的面积是36.
4.∠BAC是直角,证明如下:
∵AD⊥BC
∴∠ADB=∠ADC=90°
∴AD?+BD?=AB?,AD?+CD?=AC?
∵AD=6,BD=9,CD=4,
∴AB?=117,AC?=52.
∵BC=BD+CD=13,
∴AB?+AC?=BC?
∴∠BAC=90°.
5.10
6.∵BD⊥AC
在Rt△ABD中,BD=8,BC=10,
∴CD=6.
设
则
在Rt△ABD中,AD?+BD?=AB?,
∴,解
∴.
随堂练习
B
A
5或
或
如图,连接AC,
∵AD=4cm,CD=3cm,∠ACD=90°,
∴AC=5cm,
∴cm.
在△ABC中,∵5?+12?=13?,即AC?+BC?=AB?,
∴△ABC为直角三角形,即∠ACB=90°,
∴cm?
∴cm?
故四边形ABCD的面积为24cm?.
12.(1)11
(2)如图,分别以AC、BC、AB为一边作正方形ACED、正方形BCNM、正方形ABHF;
延长DE交MN于点Q,连接QC至AG、BP位置,直线GP分别交AF、BH于点T、S,则四边形ABST即为所求.
13.(1)∵等腰三角形ABC中,AB=AC,BD⊥AC,
∴∠ABC=∠C,∠ADB=90°
∵∠A=48°
∴∠ABC=∠C=66°,∠ABD=42°
∴∠CBD=24°
(2)∵BD⊥AC
∴∠BDC=90°
∵BC=15,BD=12
∴CD=9
设AB=,则AD=
∵∠ADB=90°,BD=12
∴,解,即AB=
14.如图,连接BD,过点B作DE边上的高BF,则BF=
∵
又
∴
∴
15.(1)如图(1),连接PB
∵∠ACB=90°,BC=6,AB=10
∴AC=8
∵AP=4t
∴CP=8-4t
∵PA=PB=4t
∴(4t)?=6?+(8-4t)?
∴t=.
(2)如图(2)所示,作PH⊥AB于点H,
∵点P在∠BAC的角平分线上,
∴PC=PH=4t-8,PB=14-4t,
可证△ACP≌△AHP
∴AH=AC=8
∴BH=2
∴2?+(4t-8)?=(14-4t)?∴t=
(3)t的值为.
专项提优训练:
A
B
3.因为△ADE与△AFE关于AE对称,
所以DE=FE,AD=AF.
因为BC=20cm,AB=16cm,
∴CD=16cm,AD=AF=20cm.
在Rt△ABF中,由勾股定理,得BF=12cm,
所以CF=20-12=8cm
设CE=x,则DE=EF=16-x,
在Rt△CEF中,由勾股定理得:(16-x)?=64+x?
解得x=6.
所以EC=6cm.
故EC=6cm,CF=8cm.
4.
C
5.
15
6.如图,把长方体的面DCC′D沿棱CD展开至面ABCD上,构成矩形ABC′D′,则点A到C′的最短距离为AC′的长度.
由勾股定理得:AF′?=AD′?+D′C′?=8?+6?=100
∴AC′=10cm
即最短长度为10cm
7.(1)如图,木柜的表面展开图是两个矩形,和.蚂蚁能够最快到达目的地的可能路径有如图所示的和两种.
(2);;,最短路径长是.
知识导图
专题一:勾股定理及其证明
1.如图,以直角三角形为边,向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足图形个数有(
)
2.如图(1),这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图(2),其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为
.
专题二:勾股定理的逆定理
3.一个零件的形状如图(1)所示,按规定这个零件中,∠A和∠DBC都应为直角.工人师傅量得这个零件各边长如图(2)所示.
你认为这个零件符号要求吗?为什么?
求这个零件的面积.
4.如图,在△ABC中,AD⊥BC,垂足为D.如果AD=6,BD=9,CD=4,那么∠BAC是直角吗?证明你的结论.
专题三:勾股定理及逆定理的简单运用
5.如图,一个上方无盖的正方体盒子紧贴地面,一只蚂蚁由盒外AE的中点处出发,沿着盒子表面爬行到盒内的点C处,一只正方体的棱长为4,则这只蚂蚁爬行的最短距离是
.
6.如图,在等腰三角形ABC中,AB=AC,BC=10,BD⊥AC于点D,且BD=8,求△ABC的面积.
随堂小练习
7.下列各组数中,是勾股数的(
)
A.
12、15、18
B.11、60、61
C.15、16、17
D.12、35、36
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M,若CM=3,则的值为(
)
36
B.
9
C.
6
D.18
9.直角三角形的两边为3和4,则该三角形的第三边为
.
10.定义:如图,点M、N把线段AB分割成三条线段AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.若AM=1,MN=2,则BN的长为
.
11.如图,AB=13cm,AD=4cm,CD=3cm,BC=12cm,∠D=90°.求四边形ABCD的面积.
12.如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
(1)计算的值等于
;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的长方形,使该长方形的面积等于,并简要说明画图方法.(不要求证明)
13.如图,在等腰三角形ABC中,已知AB=AC,BD⊥AC于点D.
(1)若∠A=48°,求∠CBD的度数;
(2)若BC=15,BD=2,求AB的长.
14.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现:当两个全等的直角三角形如图(1)或图(2)摆放时,都可以用“面积法”来证明.下面是小聪利用图(1)证明勾股定理的过程:
将两个全等的直角三角形按图(1)所示摆放,其中∠DAB=90°,求证:.
证明:连接DB,过点D作BC边上的高DF,
则DF=EC=,
∵
又
∴
∴
请参照上述证法,利用图(2)完成下面的证明.
将两个全等的直角三角形按图(2)所示摆放,其中∠DAB=90°.求证.
15.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A-C-B-A运动,设时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,当△BCP为等腰三角形时,请直接写出t的值.
专项提优特训:
类型一:利用勾股定理解决平面图形的折叠问题
1.如图,将长方形ABCD沿EF折叠,使顶点C恰好在AB边的中点C′上,若AB=6,BC=9,则BF的长为(
).
4
B.
C.4.5
D.
5
2.如图,在长方形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在C′处,BC′交AD于点E,则线段DE的长为(
).
A.
3
B.
C.
5
D.
3.为了向建国七十一周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班里开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作的第一、二个步骤是:
①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD;
②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处.
请你根据①②步骤解答下列问题:计算EC、FC的长.
类型二:利用勾股定理解决立体图形的展开问题
4.如图,圆柱的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是(
).
6cm
B.
12cm
C.
13cm
D.
16cm
5.如图,圆柱形玻璃杯高为12cm,底边周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为
cm.
6.一位同学要用彩带装饰一个长方体礼盒.长方体高6cm,底面是边长为4cm的正方形,从顶点A到顶点C′如何贴彩带用的彩带最短?最短长度是多少?
7.如图,一个长方体形状的木柜在墙角处(与墙面和底面均没有缝隙),有一只蚂蚁从柜脚A处沿着木柜表面爬到柜脚处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,=5时,求蚂蚁爬过的最短路径的长.
参考答案
D
10
(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB?+AD?=BD?,BD?+BC?=DC?,
∴△ABD、△BDC都是直角三角形.
∴∠A=90°,∠DBC=90°.
故这个零件符合要求.
(2)这个零件的面积为
故这个零件的面积是36.
4.∠BAC是直角,证明如下:
∵AD⊥BC
∴∠ADB=∠ADC=90°
∴AD?+BD?=AB?,AD?+CD?=AC?
∵AD=6,BD=9,CD=4,
∴AB?=117,AC?=52.
∵BC=BD+CD=13,
∴AB?+AC?=BC?
∴∠BAC=90°.
5.10
6.∵BD⊥AC
在Rt△ABD中,BD=8,BC=10,
∴CD=6.
设
则
在Rt△ABD中,AD?+BD?=AB?,
∴,解
∴.
随堂练习
B
A
5或
或
如图,连接AC,
∵AD=4cm,CD=3cm,∠ACD=90°,
∴AC=5cm,
∴cm.
在△ABC中,∵5?+12?=13?,即AC?+BC?=AB?,
∴△ABC为直角三角形,即∠ACB=90°,
∴cm?
∴cm?
故四边形ABCD的面积为24cm?.
12.(1)11
(2)如图,分别以AC、BC、AB为一边作正方形ACED、正方形BCNM、正方形ABHF;
延长DE交MN于点Q,连接QC至AG、BP位置,直线GP分别交AF、BH于点T、S,则四边形ABST即为所求.
13.(1)∵等腰三角形ABC中,AB=AC,BD⊥AC,
∴∠ABC=∠C,∠ADB=90°
∵∠A=48°
∴∠ABC=∠C=66°,∠ABD=42°
∴∠CBD=24°
(2)∵BD⊥AC
∴∠BDC=90°
∵BC=15,BD=12
∴CD=9
设AB=,则AD=
∵∠ADB=90°,BD=12
∴,解,即AB=
14.如图,连接BD,过点B作DE边上的高BF,则BF=
∵
又
∴
∴
15.(1)如图(1),连接PB
∵∠ACB=90°,BC=6,AB=10
∴AC=8
∵AP=4t
∴CP=8-4t
∵PA=PB=4t
∴(4t)?=6?+(8-4t)?
∴t=.
(2)如图(2)所示,作PH⊥AB于点H,
∵点P在∠BAC的角平分线上,
∴PC=PH=4t-8,PB=14-4t,
可证△ACP≌△AHP
∴AH=AC=8
∴BH=2
∴2?+(4t-8)?=(14-4t)?∴t=
(3)t的值为.
专项提优训练:
A
B
3.因为△ADE与△AFE关于AE对称,
所以DE=FE,AD=AF.
因为BC=20cm,AB=16cm,
∴CD=16cm,AD=AF=20cm.
在Rt△ABF中,由勾股定理,得BF=12cm,
所以CF=20-12=8cm
设CE=x,则DE=EF=16-x,
在Rt△CEF中,由勾股定理得:(16-x)?=64+x?
解得x=6.
所以EC=6cm.
故EC=6cm,CF=8cm.
4.
C
5.
15
6.如图,把长方体的面DCC′D沿棱CD展开至面ABCD上,构成矩形ABC′D′,则点A到C′的最短距离为AC′的长度.
由勾股定理得:AF′?=AD′?+D′C′?=8?+6?=100
∴AC′=10cm
即最短长度为10cm
7.(1)如图,木柜的表面展开图是两个矩形,和.蚂蚁能够最快到达目的地的可能路径有如图所示的和两种.
(2);;,最短路径长是.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
