人教版数学九年级下册28.1.2正弦、余弦、正切函数的简单应用教案
文档属性
| 名称 | 人教版数学九年级下册28.1.2正弦、余弦、正切函数的简单应用教案 |  | |
| 格式 | zip | ||
| 文件大小 | 49.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 08:33:12 | ||
图片预览


文档简介
正弦余弦正切的简单应用教学设计
一、教材分析
正弦余弦正切的简单应用是在学生学习了勾股定理和锐角三角函数的基础上,探究简单应用正弦、余弦、正切函数的一般方法和思路。它是前面知识的综合运用。
通过本节课学习,不仅可以巩固勾股定理和锐角三角函数等相关知识,初步获得解决问题的方法和经验,而且还让学生进一步体会数形结合的思想,为本章的后续学习作了铺垫。
二、教学目标
1.
进一步巩固锐角三角函数的定义,并能灵活运用定义进行有关计算。
2.
通过学习牢记特殊角的三角函数值,并能进行有关计算。
3.
通过学习进一步理解直角三角形的边角关系,并能进行解直角三角形的知识简单应用。
三、教学重难点
教学重点:正弦、余弦、正切函数的简单应用。
教学难点:灵活运用直角三角形中的边角关系解决问题。
四、学情分析
学生已经学习了勾股定理和锐角三角函数,已经有了相应的知识储备,因此,对本节课的学习不会很费力。学生在心理上对直角三角形中的边角关系已经有了初步认识,只要教师引导得当,应该比较容易接受。
五、教学过程
(一)复习旧知,引人新课
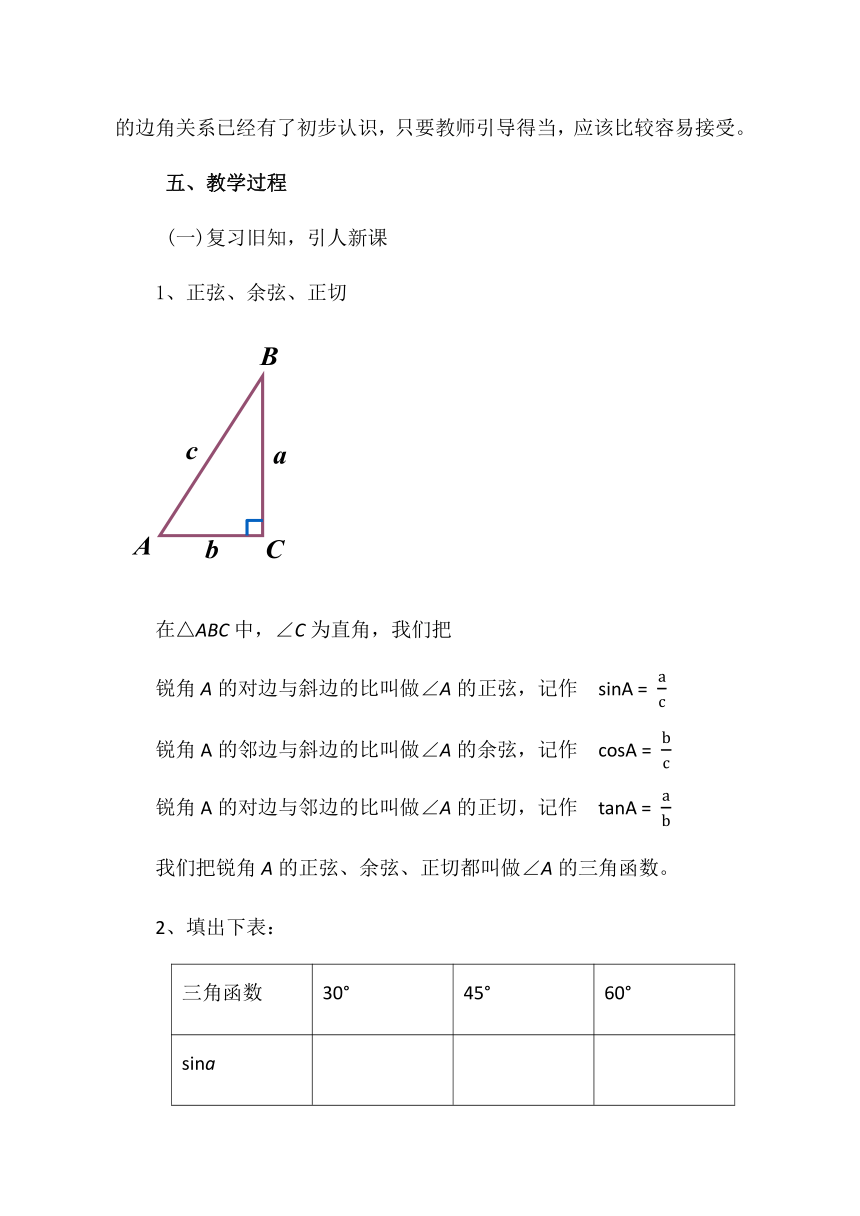
1、正弦、余弦、正切
在△ABC中,∠C为直角,我们把
锐角A的对边与斜边的比叫做∠A的正弦,记作
sinA
=
锐角A的邻边与斜边的比叫做∠A的余弦,记作
cosA
=
锐角A的对边与邻边的比叫做∠A的正切,记作
tanA
=
我们把锐角A的正弦、余弦、正切都叫做∠A的三角函数。
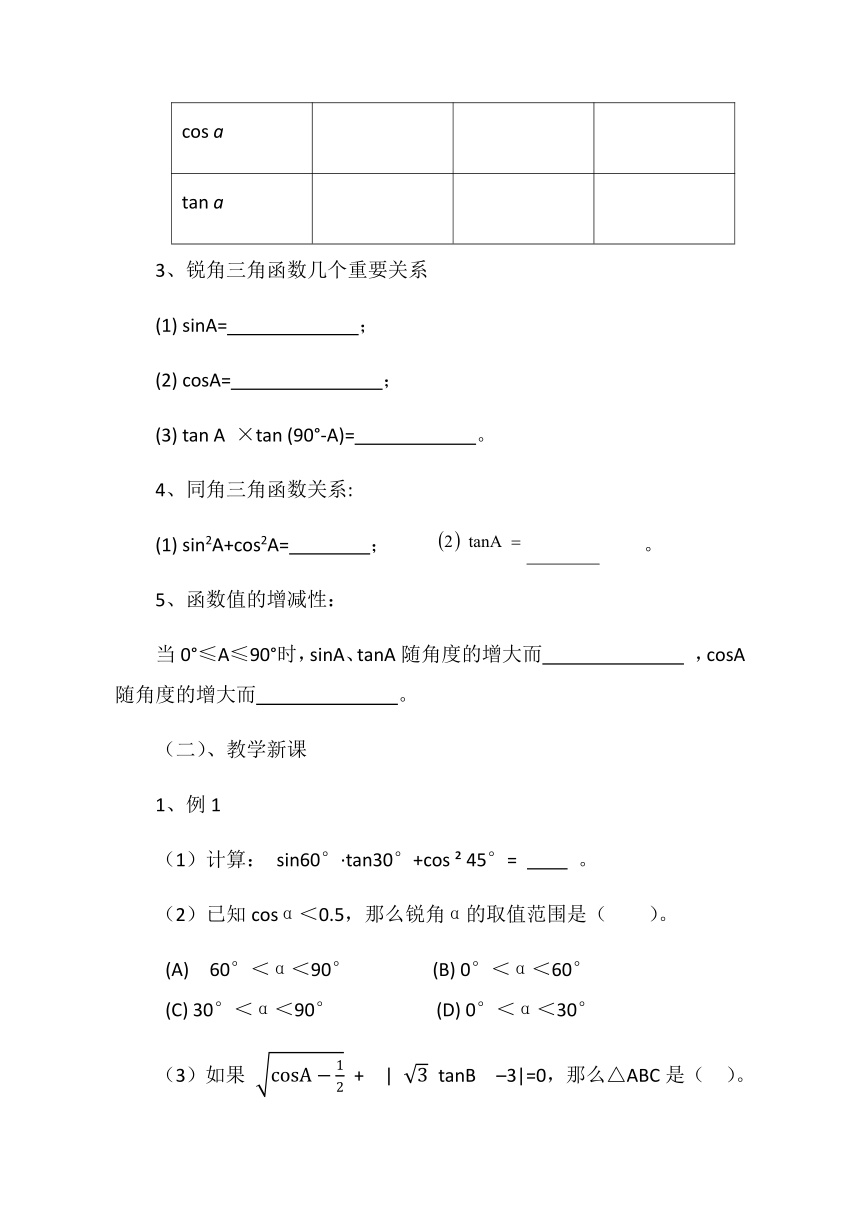
2、填出下表:
三角函数
30°
45°
60°
sina
cos
a
tan
a
3、锐角三角函数几个重要关系
(1)
sinA=
;
(2)
cosA=
;
(3)
tan
A
×tan
(90°-A)=
。
4、同角三角函数关系:
(1)
sin2A+cos2A=
;
。
5、函数值的增减性:
当0°≤A≤90°时,sinA、tanA随角度的增大而
,cosA随角度的增大而
。
(二)、教学新课
1、例1
(1)计算:
sin60°·tan30°+cos
?
45°=
。
(2)已知cosα<0.5,那么锐角α的取值范围是(
)。
(A)
60°<α<90°
(B)
0°<α<60°
(C)
30°<α<90°
(D)
0°<α<30°
(3)如果
+
|
tanB
–3|=0,那么△ABC是(
)。
(A)直角三角形
(B)锐角三角形
(C)钝角三角形
(D)等边三角形。
2、锐角三角函数的应用练习
(1)已知角,求值
①2sin30°+3tan30°+tan45°
②
cos245°+
tan60°cos30°
(2)已知三角函数值,求角
①已知
tanA=
,求锐角A。
②已知2cosA
-
=
0
,求锐角A的度数
。
(3)确定函数值的范围
①在Rt△ABC中∠C=90°,当
锐角A>45°时,sinA的值(
)。
(A)0<sinA<
(B)
<sinA<1
(C)
0<sinA<
(D)
<sinA<1
②
当锐角A>30°时,cosA的值(
)。
(A)0<cosA<
(B)
<cosA<1
(C)
0<cosA<
(D)
<cosA<1
(4)确定角的范围
①当∠A为锐角,且tanA的值大于
时,∠A(
)
(A)0°<∠A<30°
(B)30°<∠A<90°
(C)0
°<∠A<60°
(D)60°<∠A<90
②当∠A为锐角,且sinA=,
那么(
)
(A)0°<∠A<
30
°
(B)
30°<∠A<45°
(C)45°<∠A≤
60
°
(D)
60°<∠A≤
90
°
(5)三角函数的简单应用
①.
分别求出图中∠A的正弦值、余弦值和正切值
②.
若cosA=
,
且∠B=90°-∠A,则sinB=____________。
③.
在△ABC中,
∠A、
∠B都是锐角,且sinA=cosB,那么△ABC一定是_________三角形。
3、教学例2
例2、如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6,求:BC的长。
4、拓展练习
(1)如图:在等腰△ABC中,AB=AC=5,BC=6,求:
sinB,cosB,tanB
。
(2)在Rt△ABC中,∠C=900,BC=20,sinA=
,求△ABC的周长。
六、课堂小结
1.锐角三角函数定义:
tanA=
sinA=
cosA=
2.请思考:在Rt△ABC中,∠C为直角,sinA和cosB有什么关系?
3.定义中应该注意的几个问题
(1)sinA,cosA,tanA
是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形);
(2)sinA,cosA,tanA
是一个完整的符号,表示∠A的正弦、余弦、正切,习惯省去“∠”号;
(3)sinA,cosA,tanA是一个比值.注意比的顺序,且sinA,cosA,tanA均>0,无单位;
(4)sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
七、作业
1、计算
(1)
tan30°+cos45°+tan60°
(2)
tan30°·
tan60°+
cos230°
2、如图:在Rt△A中,∠C=900,AC=10,cosA=,求:AB,sinB。
3、在Rt△ABC中,∠C=90°,AB=15,sinA=
,求AC和BC。
4、在等腰△ABC中,AB=AC=13,BC=10,求sinB,cosB。
一、教材分析
正弦余弦正切的简单应用是在学生学习了勾股定理和锐角三角函数的基础上,探究简单应用正弦、余弦、正切函数的一般方法和思路。它是前面知识的综合运用。
通过本节课学习,不仅可以巩固勾股定理和锐角三角函数等相关知识,初步获得解决问题的方法和经验,而且还让学生进一步体会数形结合的思想,为本章的后续学习作了铺垫。
二、教学目标
1.
进一步巩固锐角三角函数的定义,并能灵活运用定义进行有关计算。
2.
通过学习牢记特殊角的三角函数值,并能进行有关计算。
3.
通过学习进一步理解直角三角形的边角关系,并能进行解直角三角形的知识简单应用。
三、教学重难点
教学重点:正弦、余弦、正切函数的简单应用。
教学难点:灵活运用直角三角形中的边角关系解决问题。
四、学情分析
学生已经学习了勾股定理和锐角三角函数,已经有了相应的知识储备,因此,对本节课的学习不会很费力。学生在心理上对直角三角形中的边角关系已经有了初步认识,只要教师引导得当,应该比较容易接受。
五、教学过程
(一)复习旧知,引人新课
1、正弦、余弦、正切
在△ABC中,∠C为直角,我们把
锐角A的对边与斜边的比叫做∠A的正弦,记作
sinA
=
锐角A的邻边与斜边的比叫做∠A的余弦,记作
cosA
=
锐角A的对边与邻边的比叫做∠A的正切,记作
tanA
=
我们把锐角A的正弦、余弦、正切都叫做∠A的三角函数。
2、填出下表:
三角函数
30°
45°
60°
sina
cos
a
tan
a
3、锐角三角函数几个重要关系
(1)
sinA=
;
(2)
cosA=
;
(3)
tan
A
×tan
(90°-A)=
。
4、同角三角函数关系:
(1)
sin2A+cos2A=
;
。
5、函数值的增减性:
当0°≤A≤90°时,sinA、tanA随角度的增大而
,cosA随角度的增大而
。
(二)、教学新课
1、例1
(1)计算:
sin60°·tan30°+cos
?
45°=
。
(2)已知cosα<0.5,那么锐角α的取值范围是(
)。
(A)
60°<α<90°
(B)
0°<α<60°
(C)
30°<α<90°
(D)
0°<α<30°
(3)如果
+
|
tanB
–3|=0,那么△ABC是(
)。
(A)直角三角形
(B)锐角三角形
(C)钝角三角形
(D)等边三角形。
2、锐角三角函数的应用练习
(1)已知角,求值
①2sin30°+3tan30°+tan45°
②
cos245°+
tan60°cos30°
(2)已知三角函数值,求角
①已知
tanA=
,求锐角A。
②已知2cosA
-
=
0
,求锐角A的度数
。
(3)确定函数值的范围
①在Rt△ABC中∠C=90°,当
锐角A>45°时,sinA的值(
)。
(A)0<sinA<
(B)
<sinA<1
(C)
0<sinA<
(D)
<sinA<1
②
当锐角A>30°时,cosA的值(
)。
(A)0<cosA<
(B)
<cosA<1
(C)
0<cosA<
(D)
<cosA<1
(4)确定角的范围
①当∠A为锐角,且tanA的值大于
时,∠A(
)
(A)0°<∠A<30°
(B)30°<∠A<90°
(C)0
°<∠A<60°
(D)60°<∠A<90
②当∠A为锐角,且sinA=,
那么(
)
(A)0°<∠A<
30
°
(B)
30°<∠A<45°
(C)45°<∠A≤
60
°
(D)
60°<∠A≤
90
°
(5)三角函数的简单应用
①.
分别求出图中∠A的正弦值、余弦值和正切值
②.
若cosA=
,
且∠B=90°-∠A,则sinB=____________。
③.
在△ABC中,
∠A、
∠B都是锐角,且sinA=cosB,那么△ABC一定是_________三角形。
3、教学例2
例2、如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6,求:BC的长。
4、拓展练习
(1)如图:在等腰△ABC中,AB=AC=5,BC=6,求:
sinB,cosB,tanB
。
(2)在Rt△ABC中,∠C=900,BC=20,sinA=
,求△ABC的周长。
六、课堂小结
1.锐角三角函数定义:
tanA=
sinA=
cosA=
2.请思考:在Rt△ABC中,∠C为直角,sinA和cosB有什么关系?
3.定义中应该注意的几个问题
(1)sinA,cosA,tanA
是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形);
(2)sinA,cosA,tanA
是一个完整的符号,表示∠A的正弦、余弦、正切,习惯省去“∠”号;
(3)sinA,cosA,tanA是一个比值.注意比的顺序,且sinA,cosA,tanA均>0,无单位;
(4)sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
七、作业
1、计算
(1)
tan30°+cos45°+tan60°
(2)
tan30°·
tan60°+
cos230°
2、如图:在Rt△A中,∠C=900,AC=10,cosA=,求:AB,sinB。
3、在Rt△ABC中,∠C=90°,AB=15,sinA=
,求AC和BC。
4、在等腰△ABC中,AB=AC=13,BC=10,求sinB,cosB。
