北师大版八年级数学下册 第3章 图形的平移与旋转 单元检测试题 (word版 含解析)
文档属性
| 名称 | 北师大版八年级数学下册 第3章 图形的平移与旋转 单元检测试题 (word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 257.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:07:01 | ||
图片预览



文档简介
106172000123190000第3章 图形的平移与旋转 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
?1. 若使△ABC各顶点在直角坐标系中的纵坐标保持不变,横坐标比原来都小5,则此三角形( )
A.向上平移5个单位 B.向左平移5个单位
C.向下平移5个单位 D.向右平移5个单位
2. 在平面直角坐标系中,将点A(-2,?3)向上平移3个单位长度,那么平移后对应的点A'的坐标是( )
A.(-2,?-3) B.(-2,?6) C.(1,?3) D.(-2,?1)
?
3. 将直线y=2x-3向右平移2个单位,在向上平移3个单位后,所得的直线的表达式为(? ? ? ? ? )
A.y=2x-4 B.y=2x+4 C.y=2x+2 D.y=2x-2
?
4. 如图,将一块斜边长为12cm,∠B=60?的直角三角板ABC,绕点C沿逆时针方向旋转90?至△'B'C'的位置,再沿CB向右平移,使点B'刚好落在斜边AB上,那么此三角板向右平移的距离是( )
A.6-23 B.23 C.4-3 D.3
?
5. 线段MN是由线段EF经过平移得到的,若点E(-1,?3)的对应点M(2,?5),则点F(-3,?-2)的对应点N的坐标是( )
A.(-1,?0) B.(-6,?0) C.(0,?-4) D.(0,?0)
?
6. 在以下现象中:①水管里水的流动;②滑雪运动员在平坦的雪地上滑行;③射出的子弹;④火车在笔直的铁轨上行驶.其中是平移的是( )
A.①② B.①③ C.②③ D.②④
?
7. 点P(2,?-3)向左平移1个单位,再向下平移3个单位,则所得的点坐标为( )
A.(3,?0) B.(1,?6) C.(3,?-6) D.(1,?-6)
?
8. 如图的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
A. B. C. D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
9. 如图是中央电视台“大风车”栏目标志的一部分,由图形旋转的知识可知,这个图形可以看作是一个“半圆”图形绕着________,顺次旋转________度形成的. ?
10. 正八边形至少旋转________度后能与自身重合,它________(填“是”或“不是”)中心对称图形.
?
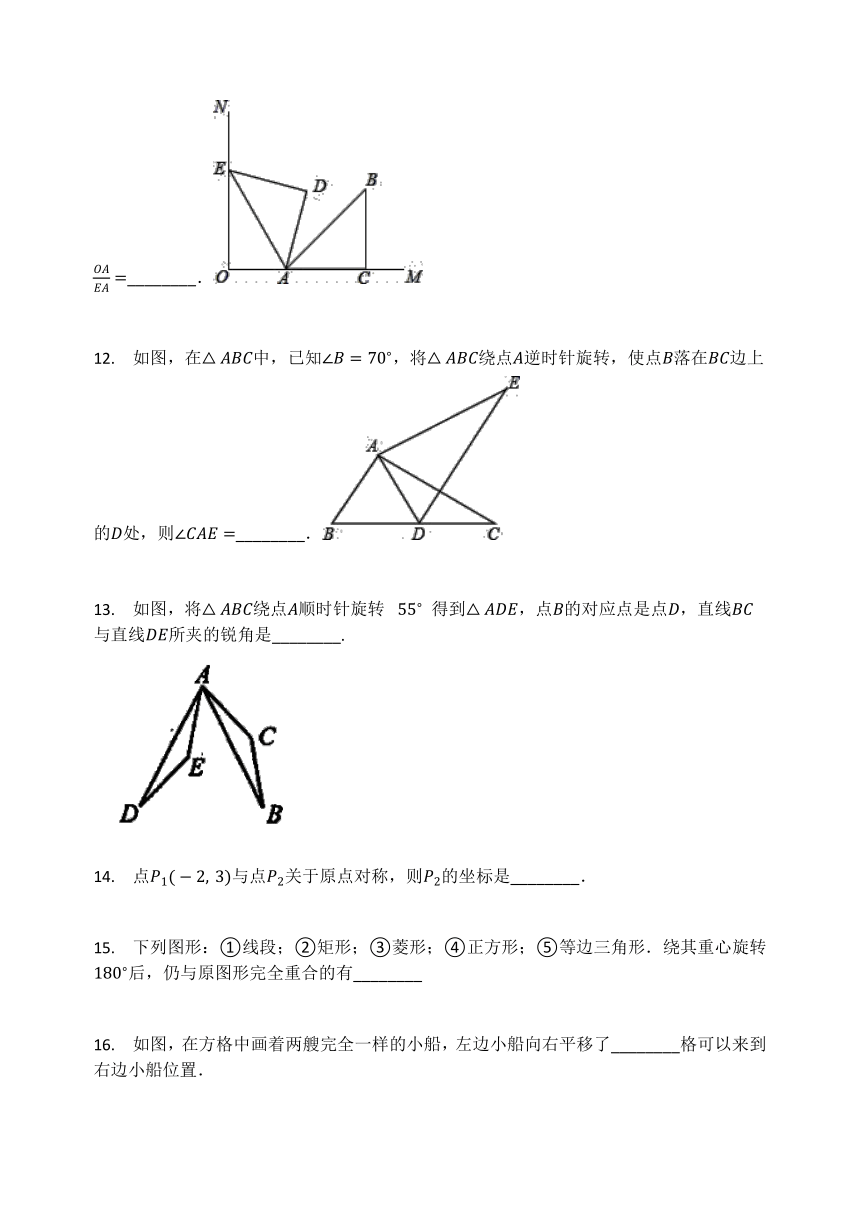
11. 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90?,边AC在OM上,将△ACB绕点A逆时针旋转75?,使得点B的对应点E恰好落在ON上,则OAEA=________.
?
12. 如图,在△ABC中,已知∠B=70?,将△ABC绕点A逆时针旋转,使点B落在BC边上的D处,则∠CAE=________.
?
13. 如图,将△ABC绕点A顺时针旋转 ?55? 得到△ADE,点B的对应点是点D,直线BC与直线DE所夹的锐角是________.
?
14. 点P1(-2,?3)与点P2关于原点对称,则P2的坐标是________.
?
15. 下列图形:①线段;②矩形;③菱形;④正方形;⑤等边三角形.绕其重心旋转180?后,仍与原图形完全重合的有________
?
16. 如图,在方格中画着两艘完全一样的小船,左边小船向右平移了________格可以来到右边小船位置.
?
17. 如图,△ABC与△A'B'C'关于点O成中心对称,∠ABC=45?,∠B'C'A'=80?,∠BAC=________??.
?
18. 如图所示,该五角星可以看作是由一个四边形经过________次旋转,每次至少旋转________得到的,所以它是________对称图形.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 在如图方格纸中,选择标有序号1,2,3,4中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是________.
?
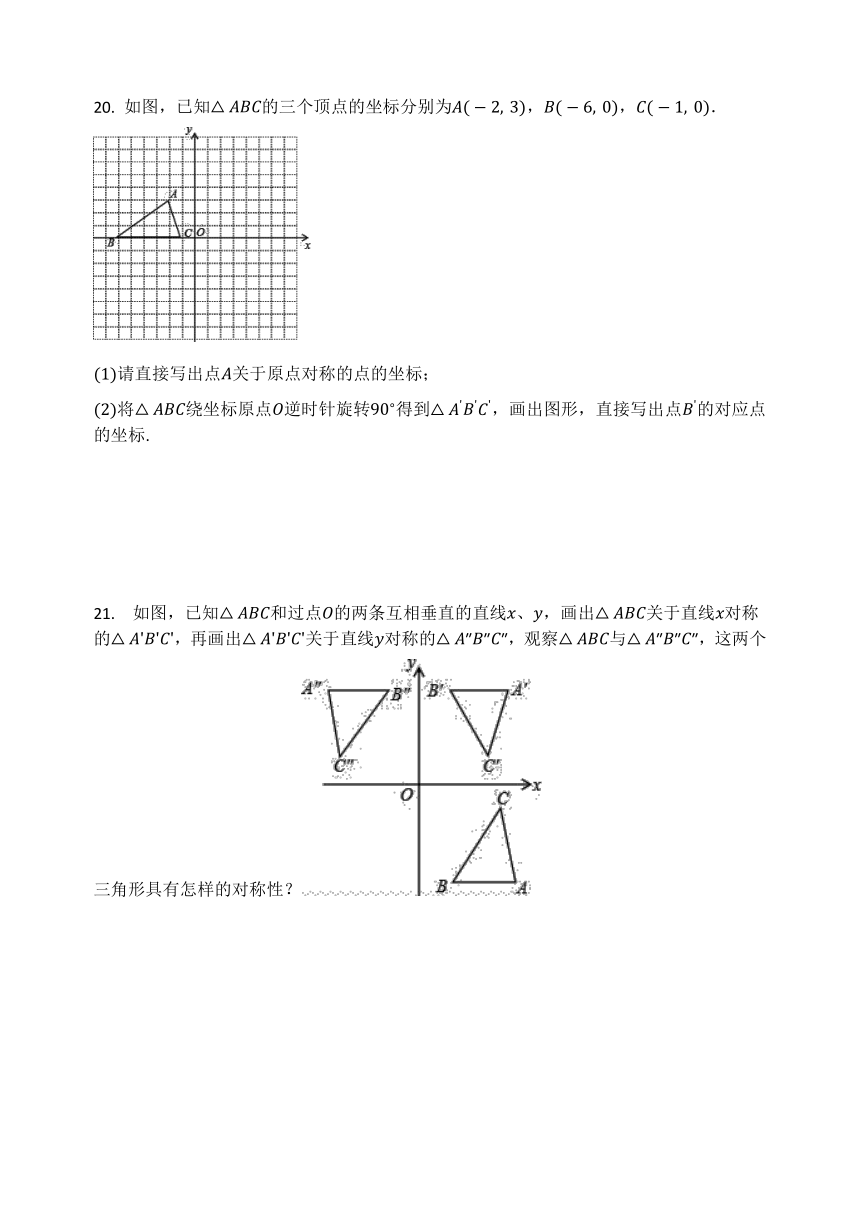
20. 如图,已知△ABC的三个顶点的坐标分别为A(-2,?3),B(-6,?0),C(-1,?0).
(1)请直接写出点A关于原点对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90?得到△A'B'C',画出图形,直接写出点B'的对应点的坐标.
?
21. 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A'B'C',再画出△A'B'C'关于直线y对称的△A″B″C″,观察△ABC与△A″B″C″,这两个三角形具有怎样的对称性?
?
22. 如图中的△DCE是由△ACB经一次或两次变换得到的,你能指出用的是什么变换吗?
?
23. 在一块长方形草地上,有人设计了如图1、2、3所示的三条不同的小路,但任何地方小路的水平宽度都是m.问长方形草地做路后,花草部分的面积哪个大?为什么?
?
24. 如图,在一块长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少?并说明你的猜想是正确的.
?
25. 如图1,在平面直角坐标系中,点A、B的坐标分别为(-1,?0)、(3,?0),现将线段AB向上平移2个单位,再向右平移1个单位,得到线段CD,连接AC、BD.
(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;
(2)如图2,在y轴上是否存在一点P,连接PA、PB,使S△PAB=S四边形ABDC,若存在这样的一点,求出点P的坐标;若不存在,试说明理由.
(3)若点Q在线段CD上移动(不包括C、D两点),QO与线段CD、AB所成的角∠2与∠1如图3所示,给出下列两个结论:①∠2+∠1的值不变,②∠1∠2的值不变,其中只有一个结论是正确的,请你找出这个结论.
参考答案
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【答案】
B
【解答】
解:要使△ABC在直角坐标系中的纵坐标保持不变,横坐标比原来小5,
则△ABC向左平移5个单位.
故选:B.
2.
【答案】
B
【解答】
解:∵ 点(-2,?3)向上平移3个单位,
∴ 平移后的点的坐标为:(-2,?3+3),
即(-2,?6),
故选B.
3.
【答案】
A
【解答】
解:y=2x-2-3+3=2x-4,
化简,得:y=2x-4,
故选A.
4.
【答案】
A
【解答】
解:过点B'作BC的平行线交AB于B″,如图,
在Rt△ABC中,∵ ∠B=60?,
∴ ∠A=30?,
∴ BC=12AB=12×12=6,
∴ AC=3BC=63,
∵ △ABC,绕点C沿逆时针方向旋转90?至△'B'C'的位置,
∴ ∠A'CA=90?,CB'=CB=6,
∴ 点A'、C、B共线,AB'=AC-CB'=63-6,
∵ B'B″?//?BC,
∴ ∠AB'B″=90?,
在Rt△AB'B″中,∵ ∠A=30?,
∴ B'B″=33AB'=33×(63-6)=6-23,
即此三角板向右平移的距离为(6-23)cm.
故选A.
5.
【答案】
D
【解答】
线段MN是由线段EF经过平移得到的,点E(-1,?3)的对应点M(2,?5),故各对应点之间的关系是横坐标加3,纵坐标加2,
∴ 点N的横坐标为:-3+3=0;点N的纵坐标为-2+2=0;
即点N的坐标是(0,?0).
6.
【答案】
D
【解答】
解:(1)水管不一定是笔直的,故错误;
(2)符合平移的定义,故正确;
(3)射出的子弹改变了运动方向,不符合平移的定义,故错误;
(4)火车在笔直的铁轨上行使,符合平移的定义,故正确.
所以(2)(4)正确.
故选D.
7.
【答案】
D
【解答】
∵ 点P(2,?-3)向左平移1个单位,向下平移3个单位,
∴ 2-1=1,-3-3=-6,
∴ 所得的点的坐标为(1,?-6).
8.
【答案】
B
【解答】
由题意,选项A,C,D可以通过平移,旋转得到,选项B可以通过翻折,平移,旋转得到.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
9.
【答案】
O,90
【解答】
解:如图是中央电视台“大风车”栏目标志的一部分,由图形旋转的知识可知,这个图形可以看作是一个“半圆”图形绕着O,顺次旋转90度形成的,故答案为:O,90.
10.
【答案】
45,是
【解答】
解:∵ 正八边形每边所对的中心角是360?÷8=45?,
∴ 至少应将它绕中心顺时针旋转45?后与自身重合,且是中心对称图形.
故答案为:45,是.
11.
【答案】
12
【解答】
解:∵ 等腰直角三角形ACB中,∠ACB=90?,
∴ ∠CAB=45?,
∵ △ACB绕点A逆时针旋转75?得到△ADE,
∴ ∠BAE=75?,
∴ ∠OAE=180?-45?-75?=60?,
在Rt△OAE中,
∴ cos60?=OAEA=12,
故答案为12.
12.
【答案】
40?
【解答】
解:根据旋转可得AB=AD,∠BAD=∠CAE,
∵ AB=AD,∠B=70?,
∴ ∠B=∠ADB=70?,
∴ ∠BAD=180?-70?-70?=40?,
∴ ∠CAE=40?,
故答案为:40?.
13.
【答案】
55?
【解答】
解:由旋转的性质可知,直线BC与直线DE所夹的锐角即为旋转角.
故答案为:55?.
14.
【答案】
(2,?-3)
【解答】
解:点P1(-2,?3)与点P2关于原点对称,
故P2的坐标是:(2,?-3).
故答案为:(2,?-3).
15.
【答案】
①②③④
【解答】
解:根据重心和中心对称图形的概念,知
⑤不是关于重心的中心对称图形.
①、②、③、④都是关于重心的中心对称图形.
故绕其重心旋转180?后,仍与原图形完全重合的有①②③④.
16.
【答案】
6
【解答】
解:观察图形可得,左边小船向右平移了6格可以来到右边小船位置.
故答案为:6.
17.
【答案】
55
【解答】
解:∵ △ABC与△A'B'C'关于点O成中心对称,
∴ △ABC?△A'B'C',
∴ ∠BCA=∠B'C'A'=80?,
∵ ∠ABC=45?,
∴ ∠BAC=180?-45?-80?=55?,
故答案为:55.
18.
【答案】
4,72?,旋转
【解答】
解:由于有五个星,所以要由一个三角形绕中心点旋转四次,
每次至少旋转的角度为360?÷5=72?,所以它是旋转对称图形.
故答案为:4;72?;旋转.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
4
【解答】
解:由题易知,涂4.
故答案为:4.
20.
【答案】
解:(1)先关于y轴对称,纵坐标不变,横坐标为相反数,得到(2,3),
再关于x轴对称,纵坐标为相反数,横坐标不变,得到(2,-3),
故点A关于原点对称的点的坐标是(2,?-3);
(2)如图,点B'的对应点的坐标是(0,?-6).
【解答】
解:(1)先关于y轴对称,纵坐标不变,横坐标为相反数,得到(2,3),
再关于x轴对称,纵坐标为相反数,横坐标不变,得到(2,-3),
故点A关于原点对称的点的坐标是(2,?-3);
(2)如图,点B'的对应点的坐标是(0,?-6).
21.
【答案】
解:由△ABC关于直线x对称的△A'B'C',
得对应点的横坐标相同,纵坐标互为相反数.
由△A'B'C'关于直线y对称的△A″B″C″,
得对应点的纵坐标相同,横坐标互为相反数.
△ABC与△A″B″C″对应点的横坐标互为相反数,纵坐标互为相反数,
△ABC与△A″B″C″关于原点对称.
【解答】
解:由△ABC关于直线x对称的△A'B'C',
得对应点的横坐标相同,纵坐标互为相反数.
由△A'B'C'关于直线y对称的△A″B″C″,
得对应点的纵坐标相同,横坐标互为相反数.
△ABC与△A″B″C″对应点的横坐标互为相反数,纵坐标互为相反数,
△ABC与△A″B″C″关于原点对称.
22.
【答案】
解:△DCE是由△ACB绕C点顺时针旋转90?得到的;
△DCE是由△ACB绕C点顺时针旋转90?,再由△BCA沿BC翻折得到的.
【解答】
解:△DCE是由△ACB绕C点顺时针旋转90?得到的;
△DCE是由△ACB绕C点顺时针旋转90?,再由△BCA沿BC翻折得到的.
23.
【答案】
解:利用平移性质可得出:花草部分的面积都为:ab-bm.一样大.
【解答】
解:利用平移性质可得出:花草部分的面积都为:ab-bm.一样大.
24.
【答案】
解:把小路向左平移到边缘得到空白部分矩形草地的长为b-1,
故空白部分表示的草地面积=b(a-1)=ab-b.
【解答】
解:把小路向左平移到边缘得到空白部分矩形草地的长为b-1,
故空白部分表示的草地面积=b(a-1)=ab-b.
25.
【答案】
(1)解:C(0,?2)D(4,?2)
S四边形ABDC=|AB|?|CO|
=4×2
=8
(2)解:假设y轴上存在P(0,?b)点,则S△PAB=S四边形ABDC
12|AB|?|b|=8,
b=±4,
∴ P(0,?4)或P(0,?-4),
(3)解:②正确
∵ CD是由AB平移所得到的,
∴ CD?//?AB,
∴ ∠1=∠2(两直线平行,同位角相等),
∴ ∠1∠2=1(恒等于1).
【解答】
(1)解:C(0,?2)D(4,?2)
S四边形ABDC=|AB|?|CO|
=4×2
=8
(2)解:假设y轴上存在P(0,?b)点,则S△PAB=S四边形ABDC
12|AB|?|b|=8,
b=±4,
∴ P(0,?4)或P(0,?-4),
(3)解:②正确
∵ CD是由AB平移所得到的,
∴ CD?//?AB,
∴ ∠1=∠2(两直线平行,同位角相等),
∴ ∠1∠2=1(恒等于1).
(满分120分;时间:120分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
?1. 若使△ABC各顶点在直角坐标系中的纵坐标保持不变,横坐标比原来都小5,则此三角形( )
A.向上平移5个单位 B.向左平移5个单位
C.向下平移5个单位 D.向右平移5个单位
2. 在平面直角坐标系中,将点A(-2,?3)向上平移3个单位长度,那么平移后对应的点A'的坐标是( )
A.(-2,?-3) B.(-2,?6) C.(1,?3) D.(-2,?1)
?
3. 将直线y=2x-3向右平移2个单位,在向上平移3个单位后,所得的直线的表达式为(? ? ? ? ? )
A.y=2x-4 B.y=2x+4 C.y=2x+2 D.y=2x-2
?
4. 如图,将一块斜边长为12cm,∠B=60?的直角三角板ABC,绕点C沿逆时针方向旋转90?至△'B'C'的位置,再沿CB向右平移,使点B'刚好落在斜边AB上,那么此三角板向右平移的距离是( )
A.6-23 B.23 C.4-3 D.3
?
5. 线段MN是由线段EF经过平移得到的,若点E(-1,?3)的对应点M(2,?5),则点F(-3,?-2)的对应点N的坐标是( )
A.(-1,?0) B.(-6,?0) C.(0,?-4) D.(0,?0)
?
6. 在以下现象中:①水管里水的流动;②滑雪运动员在平坦的雪地上滑行;③射出的子弹;④火车在笔直的铁轨上行驶.其中是平移的是( )
A.①② B.①③ C.②③ D.②④
?
7. 点P(2,?-3)向左平移1个单位,再向下平移3个单位,则所得的点坐标为( )
A.(3,?0) B.(1,?6) C.(3,?-6) D.(1,?-6)
?
8. 如图的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
A. B. C. D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
9. 如图是中央电视台“大风车”栏目标志的一部分,由图形旋转的知识可知,这个图形可以看作是一个“半圆”图形绕着________,顺次旋转________度形成的. ?
10. 正八边形至少旋转________度后能与自身重合,它________(填“是”或“不是”)中心对称图形.
?
11. 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90?,边AC在OM上,将△ACB绕点A逆时针旋转75?,使得点B的对应点E恰好落在ON上,则OAEA=________.
?
12. 如图,在△ABC中,已知∠B=70?,将△ABC绕点A逆时针旋转,使点B落在BC边上的D处,则∠CAE=________.
?
13. 如图,将△ABC绕点A顺时针旋转 ?55? 得到△ADE,点B的对应点是点D,直线BC与直线DE所夹的锐角是________.
?
14. 点P1(-2,?3)与点P2关于原点对称,则P2的坐标是________.
?
15. 下列图形:①线段;②矩形;③菱形;④正方形;⑤等边三角形.绕其重心旋转180?后,仍与原图形完全重合的有________
?
16. 如图,在方格中画着两艘完全一样的小船,左边小船向右平移了________格可以来到右边小船位置.
?
17. 如图,△ABC与△A'B'C'关于点O成中心对称,∠ABC=45?,∠B'C'A'=80?,∠BAC=________??.
?
18. 如图所示,该五角星可以看作是由一个四边形经过________次旋转,每次至少旋转________得到的,所以它是________对称图形.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 在如图方格纸中,选择标有序号1,2,3,4中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是________.
?
20. 如图,已知△ABC的三个顶点的坐标分别为A(-2,?3),B(-6,?0),C(-1,?0).
(1)请直接写出点A关于原点对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90?得到△A'B'C',画出图形,直接写出点B'的对应点的坐标.
?
21. 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A'B'C',再画出△A'B'C'关于直线y对称的△A″B″C″,观察△ABC与△A″B″C″,这两个三角形具有怎样的对称性?
?
22. 如图中的△DCE是由△ACB经一次或两次变换得到的,你能指出用的是什么变换吗?
?
23. 在一块长方形草地上,有人设计了如图1、2、3所示的三条不同的小路,但任何地方小路的水平宽度都是m.问长方形草地做路后,花草部分的面积哪个大?为什么?
?
24. 如图,在一块长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少?并说明你的猜想是正确的.
?
25. 如图1,在平面直角坐标系中,点A、B的坐标分别为(-1,?0)、(3,?0),现将线段AB向上平移2个单位,再向右平移1个单位,得到线段CD,连接AC、BD.
(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;
(2)如图2,在y轴上是否存在一点P,连接PA、PB,使S△PAB=S四边形ABDC,若存在这样的一点,求出点P的坐标;若不存在,试说明理由.
(3)若点Q在线段CD上移动(不包括C、D两点),QO与线段CD、AB所成的角∠2与∠1如图3所示,给出下列两个结论:①∠2+∠1的值不变,②∠1∠2的值不变,其中只有一个结论是正确的,请你找出这个结论.
参考答案
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【答案】
B
【解答】
解:要使△ABC在直角坐标系中的纵坐标保持不变,横坐标比原来小5,
则△ABC向左平移5个单位.
故选:B.
2.
【答案】
B
【解答】
解:∵ 点(-2,?3)向上平移3个单位,
∴ 平移后的点的坐标为:(-2,?3+3),
即(-2,?6),
故选B.
3.
【答案】
A
【解答】
解:y=2x-2-3+3=2x-4,
化简,得:y=2x-4,
故选A.
4.
【答案】
A
【解答】
解:过点B'作BC的平行线交AB于B″,如图,
在Rt△ABC中,∵ ∠B=60?,
∴ ∠A=30?,
∴ BC=12AB=12×12=6,
∴ AC=3BC=63,
∵ △ABC,绕点C沿逆时针方向旋转90?至△'B'C'的位置,
∴ ∠A'CA=90?,CB'=CB=6,
∴ 点A'、C、B共线,AB'=AC-CB'=63-6,
∵ B'B″?//?BC,
∴ ∠AB'B″=90?,
在Rt△AB'B″中,∵ ∠A=30?,
∴ B'B″=33AB'=33×(63-6)=6-23,
即此三角板向右平移的距离为(6-23)cm.
故选A.
5.
【答案】
D
【解答】
线段MN是由线段EF经过平移得到的,点E(-1,?3)的对应点M(2,?5),故各对应点之间的关系是横坐标加3,纵坐标加2,
∴ 点N的横坐标为:-3+3=0;点N的纵坐标为-2+2=0;
即点N的坐标是(0,?0).
6.
【答案】
D
【解答】
解:(1)水管不一定是笔直的,故错误;
(2)符合平移的定义,故正确;
(3)射出的子弹改变了运动方向,不符合平移的定义,故错误;
(4)火车在笔直的铁轨上行使,符合平移的定义,故正确.
所以(2)(4)正确.
故选D.
7.
【答案】
D
【解答】
∵ 点P(2,?-3)向左平移1个单位,向下平移3个单位,
∴ 2-1=1,-3-3=-6,
∴ 所得的点的坐标为(1,?-6).
8.
【答案】
B
【解答】
由题意,选项A,C,D可以通过平移,旋转得到,选项B可以通过翻折,平移,旋转得到.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
9.
【答案】
O,90
【解答】
解:如图是中央电视台“大风车”栏目标志的一部分,由图形旋转的知识可知,这个图形可以看作是一个“半圆”图形绕着O,顺次旋转90度形成的,故答案为:O,90.
10.
【答案】
45,是
【解答】
解:∵ 正八边形每边所对的中心角是360?÷8=45?,
∴ 至少应将它绕中心顺时针旋转45?后与自身重合,且是中心对称图形.
故答案为:45,是.
11.
【答案】
12
【解答】
解:∵ 等腰直角三角形ACB中,∠ACB=90?,
∴ ∠CAB=45?,
∵ △ACB绕点A逆时针旋转75?得到△ADE,
∴ ∠BAE=75?,
∴ ∠OAE=180?-45?-75?=60?,
在Rt△OAE中,
∴ cos60?=OAEA=12,
故答案为12.
12.
【答案】
40?
【解答】
解:根据旋转可得AB=AD,∠BAD=∠CAE,
∵ AB=AD,∠B=70?,
∴ ∠B=∠ADB=70?,
∴ ∠BAD=180?-70?-70?=40?,
∴ ∠CAE=40?,
故答案为:40?.
13.
【答案】
55?
【解答】
解:由旋转的性质可知,直线BC与直线DE所夹的锐角即为旋转角.
故答案为:55?.
14.
【答案】
(2,?-3)
【解答】
解:点P1(-2,?3)与点P2关于原点对称,
故P2的坐标是:(2,?-3).
故答案为:(2,?-3).
15.
【答案】
①②③④
【解答】
解:根据重心和中心对称图形的概念,知
⑤不是关于重心的中心对称图形.
①、②、③、④都是关于重心的中心对称图形.
故绕其重心旋转180?后,仍与原图形完全重合的有①②③④.
16.
【答案】
6
【解答】
解:观察图形可得,左边小船向右平移了6格可以来到右边小船位置.
故答案为:6.
17.
【答案】
55
【解答】
解:∵ △ABC与△A'B'C'关于点O成中心对称,
∴ △ABC?△A'B'C',
∴ ∠BCA=∠B'C'A'=80?,
∵ ∠ABC=45?,
∴ ∠BAC=180?-45?-80?=55?,
故答案为:55.
18.
【答案】
4,72?,旋转
【解答】
解:由于有五个星,所以要由一个三角形绕中心点旋转四次,
每次至少旋转的角度为360?÷5=72?,所以它是旋转对称图形.
故答案为:4;72?;旋转.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
4
【解答】
解:由题易知,涂4.
故答案为:4.
20.
【答案】
解:(1)先关于y轴对称,纵坐标不变,横坐标为相反数,得到(2,3),
再关于x轴对称,纵坐标为相反数,横坐标不变,得到(2,-3),
故点A关于原点对称的点的坐标是(2,?-3);
(2)如图,点B'的对应点的坐标是(0,?-6).
【解答】
解:(1)先关于y轴对称,纵坐标不变,横坐标为相反数,得到(2,3),
再关于x轴对称,纵坐标为相反数,横坐标不变,得到(2,-3),
故点A关于原点对称的点的坐标是(2,?-3);
(2)如图,点B'的对应点的坐标是(0,?-6).
21.
【答案】
解:由△ABC关于直线x对称的△A'B'C',
得对应点的横坐标相同,纵坐标互为相反数.
由△A'B'C'关于直线y对称的△A″B″C″,
得对应点的纵坐标相同,横坐标互为相反数.
△ABC与△A″B″C″对应点的横坐标互为相反数,纵坐标互为相反数,
△ABC与△A″B″C″关于原点对称.
【解答】
解:由△ABC关于直线x对称的△A'B'C',
得对应点的横坐标相同,纵坐标互为相反数.
由△A'B'C'关于直线y对称的△A″B″C″,
得对应点的纵坐标相同,横坐标互为相反数.
△ABC与△A″B″C″对应点的横坐标互为相反数,纵坐标互为相反数,
△ABC与△A″B″C″关于原点对称.
22.
【答案】
解:△DCE是由△ACB绕C点顺时针旋转90?得到的;
△DCE是由△ACB绕C点顺时针旋转90?,再由△BCA沿BC翻折得到的.
【解答】
解:△DCE是由△ACB绕C点顺时针旋转90?得到的;
△DCE是由△ACB绕C点顺时针旋转90?,再由△BCA沿BC翻折得到的.
23.
【答案】
解:利用平移性质可得出:花草部分的面积都为:ab-bm.一样大.
【解答】
解:利用平移性质可得出:花草部分的面积都为:ab-bm.一样大.
24.
【答案】
解:把小路向左平移到边缘得到空白部分矩形草地的长为b-1,
故空白部分表示的草地面积=b(a-1)=ab-b.
【解答】
解:把小路向左平移到边缘得到空白部分矩形草地的长为b-1,
故空白部分表示的草地面积=b(a-1)=ab-b.
25.
【答案】
(1)解:C(0,?2)D(4,?2)
S四边形ABDC=|AB|?|CO|
=4×2
=8
(2)解:假设y轴上存在P(0,?b)点,则S△PAB=S四边形ABDC
12|AB|?|b|=8,
b=±4,
∴ P(0,?4)或P(0,?-4),
(3)解:②正确
∵ CD是由AB平移所得到的,
∴ CD?//?AB,
∴ ∠1=∠2(两直线平行,同位角相等),
∴ ∠1∠2=1(恒等于1).
【解答】
(1)解:C(0,?2)D(4,?2)
S四边形ABDC=|AB|?|CO|
=4×2
=8
(2)解:假设y轴上存在P(0,?b)点,则S△PAB=S四边形ABDC
12|AB|?|b|=8,
b=±4,
∴ P(0,?4)或P(0,?-4),
(3)解:②正确
∵ CD是由AB平移所得到的,
∴ CD?//?AB,
∴ ∠1=∠2(两直线平行,同位角相等),
∴ ∠1∠2=1(恒等于1).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
