人教版八年级数学下册课件:18.2.2菱形的判定(共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2.2菱形的判定(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 14:09:49 | ||
图片预览




文档简介
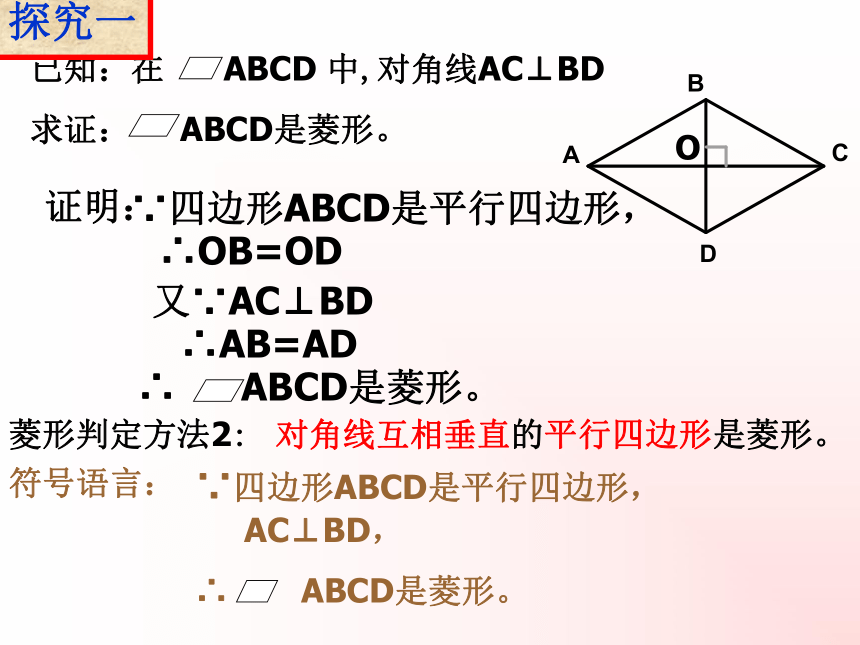
已知:在 ABCD 中,对角线AC⊥BD
求证: ABCD是菱形。
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ ABCD是菱形。
∴AB=AD
菱形判定方法2: 对角线互相垂直的平行四边形是菱形。
∵四边形ABCD是平行四边形,
AC⊥BD,
∴ ABCD是菱形。
符号语言:
O
探究一
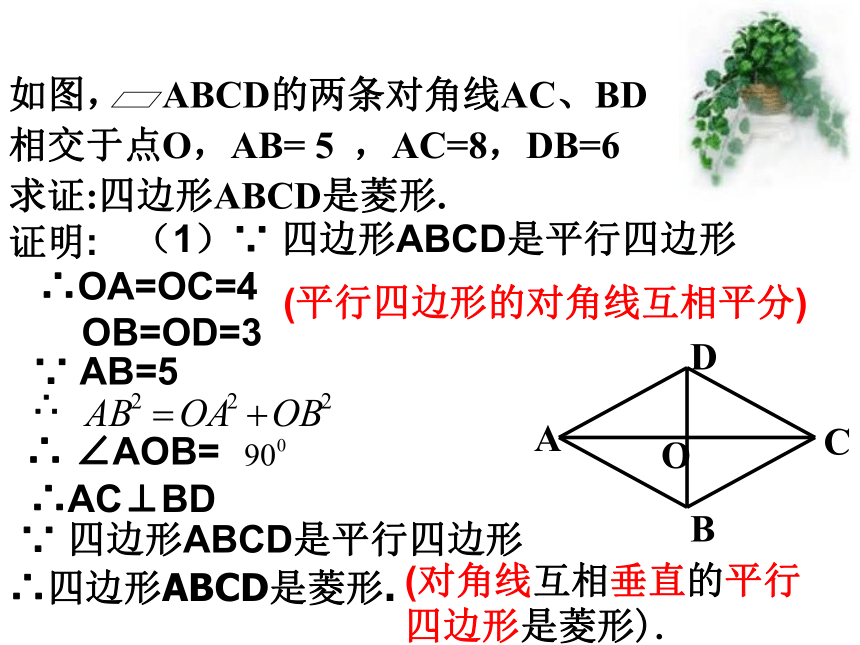
如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.
A
B
C
D
O
∴四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
∵ AB=5
∴
∴AC⊥BD
∴ ∠AOB=
∵ 四边形ABCD是平行四边形
(1)∵ 四边形ABCD是平行四边形
(平行四边形的对角线互相平分)
(对角线互相垂直的平行四边形是菱形).
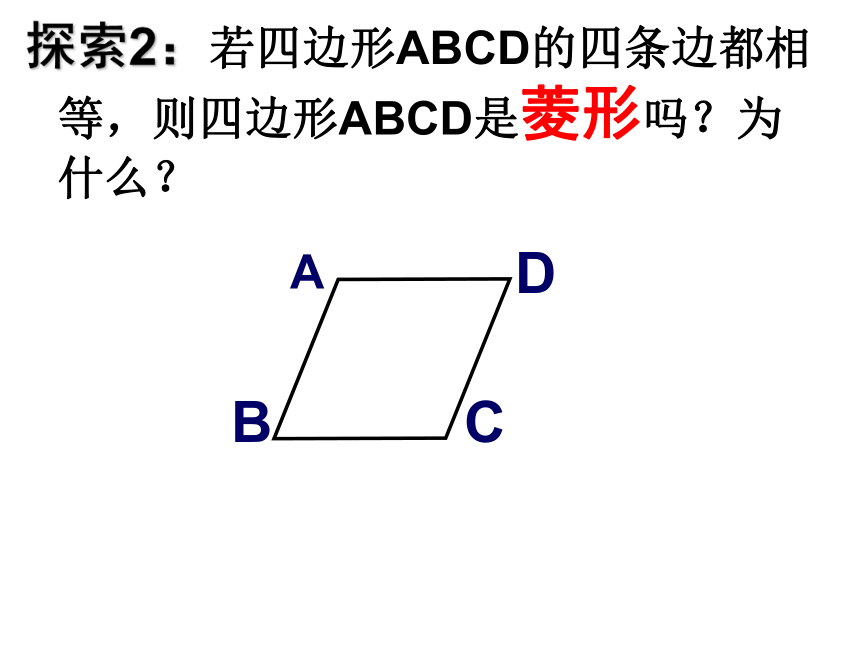
探索2:若四边形ABCD的四条边都相等,则四边形ABCD是菱形吗?为什么?
A
D
C
B
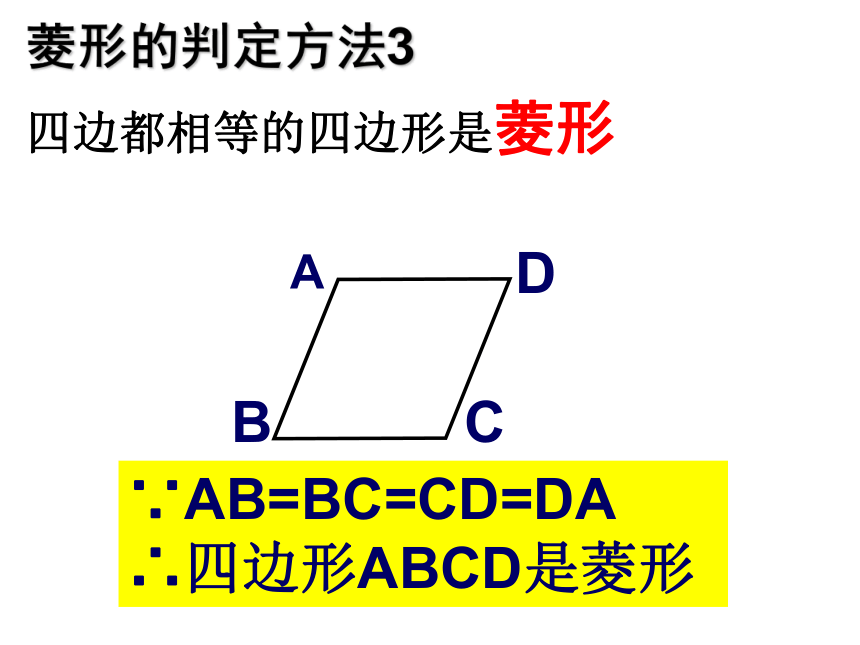
菱形的判定方法3
四边都相等的四边形是菱形
∵AB=BC=CD=DA
∴四边形ABCD是菱形
A
D
C
B
归纳
1.有一组邻边相等的 是菱形.
2.对角线互相垂直的 是菱形.
3.有四条边相等的 是菱形.
4.对角线互相垂直平分的四边形是菱形.
菱形常用的判定方法:
平行四边形
平行四边形
四边形
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
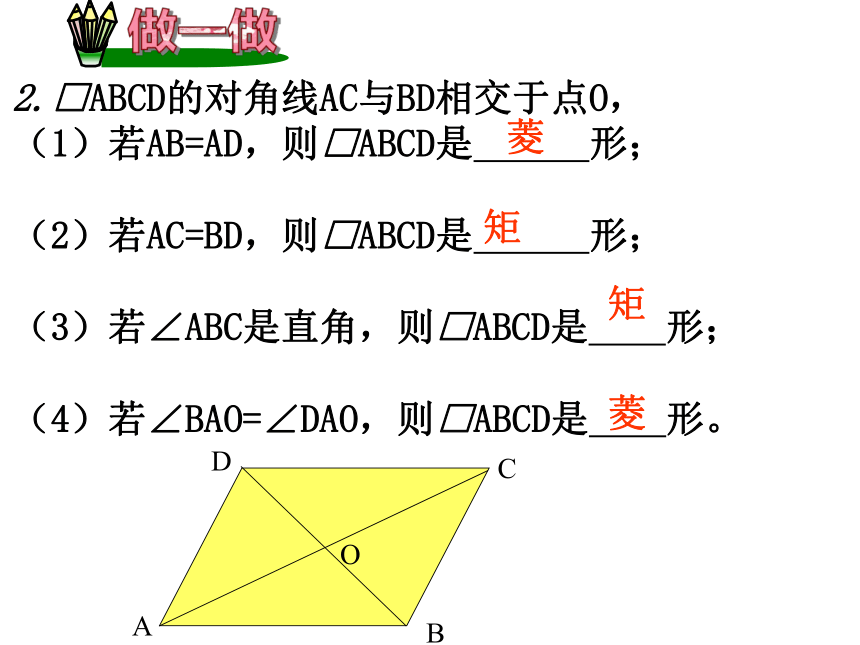
2.□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
4.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
C
5.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
D
C
B
A
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
小结:
1.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试问四边形AEDF是菱形吗?说明你的理由。
习题巩固:
A
B
C
D
E
F
1
2
3
四边形AEDF是菱形
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2
∴AE=DE
∴ □ AEDF是菱形
已知如图,AD是的角平分线,DE∥AC,DF∥AB.
证明:四边形AEDF是菱形。
对于这道,小林是这样证明的。
证明:∵AD平分,∴∠1=∠2,
∵DE∥AC,∴∠2=∠3
∵DF∥AB,∴∠1=∠4
又有AD=AD,∴△AED≌△AFD.
∴AE=AF,DE=DF. ∴四边形AEDF是菱形.
老师说小林的解题过程有错误,你能看出来吗?
⑴请你帮小林指出他的错误是什么?(先在解答过程中划出来,再说明他错误的原因)
⑵请你帮小林做出正确的解答。
A
B
C
D
O
E
2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
3.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形
B
C
A
D
O
E
M
N
如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
A
B
C
D
E
F
谢谢
如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?
2.如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,
证明:CE⊥DF.
A
B
F
N
D
M
E
C
习题巩固:
求证: ABCD是菱形。
证明:
∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ ABCD是菱形。
∴AB=AD
菱形判定方法2: 对角线互相垂直的平行四边形是菱形。
∵四边形ABCD是平行四边形,
AC⊥BD,
∴ ABCD是菱形。
符号语言:
O
探究一
如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.
A
B
C
D
O
∴四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
∵ AB=5
∴
∴AC⊥BD
∴ ∠AOB=
∵ 四边形ABCD是平行四边形
(1)∵ 四边形ABCD是平行四边形
(平行四边形的对角线互相平分)
(对角线互相垂直的平行四边形是菱形).
探索2:若四边形ABCD的四条边都相等,则四边形ABCD是菱形吗?为什么?
A
D
C
B
菱形的判定方法3
四边都相等的四边形是菱形
∵AB=BC=CD=DA
∴四边形ABCD是菱形
A
D
C
B
归纳
1.有一组邻边相等的 是菱形.
2.对角线互相垂直的 是菱形.
3.有四条边相等的 是菱形.
4.对角线互相垂直平分的四边形是菱形.
菱形常用的判定方法:
平行四边形
平行四边形
四边形
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
2.□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
4.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
C
5.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
D
C
B
A
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
小结:
1.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试问四边形AEDF是菱形吗?说明你的理由。
习题巩固:
A
B
C
D
E
F
1
2
3
四边形AEDF是菱形
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2
∴AE=DE
∴ □ AEDF是菱形
已知如图,AD是的角平分线,DE∥AC,DF∥AB.
证明:四边形AEDF是菱形。
对于这道,小林是这样证明的。
证明:∵AD平分,∴∠1=∠2,
∵DE∥AC,∴∠2=∠3
∵DF∥AB,∴∠1=∠4
又有AD=AD,∴△AED≌△AFD.
∴AE=AF,DE=DF. ∴四边形AEDF是菱形.
老师说小林的解题过程有错误,你能看出来吗?
⑴请你帮小林指出他的错误是什么?(先在解答过程中划出来,再说明他错误的原因)
⑵请你帮小林做出正确的解答。
A
B
C
D
O
E
2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
3.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.
求证:四边形ADCE是菱形
B
C
A
D
O
E
M
N
如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
A
B
C
D
E
F
谢谢
如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?
2.如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,
证明:CE⊥DF.
A
B
F
N
D
M
E
C
习题巩固:
