人教版八年级数学下册课件:19.1.1函数(共24张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.1.1函数(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 14:12:53 | ||
图片预览





文档简介
19.1.1 函数
一列动车从甲地驶往乙地,在16:17到16:22这个时段,列车以200千米/时的速度匀速行驶.在列车行驶过程中,哪些量没有变化?哪些量是在不断的变化?
在这一过程中,没有变化的量是:
列车行驶的速度不变;
从甲地到乙地的路程不变.
列车行驶的总时间不变
在这一过程中,变化了的量是:
列车行驶的时间在不断变化;
列车距离起点和终点的路程也在不断变化.
常量:
在某一变化过程中,数值保持不变的量叫做常量.
变量:
在某一变化过程中,可以取不同数值的量叫做变量.
1、下列各关系式中有常量和变量吗?
(1)直角三角形两锐角∠A ,∠B的关系式为∠A+∠B=900
(2)矩形的长a一定,面积s和宽b 的关系式为s = a b
(3)矩形的宽b一定,面积s和长a的关系式为s = a b
常量与变量不是绝对的,而是相对于一个变化过程而言的。
练一练
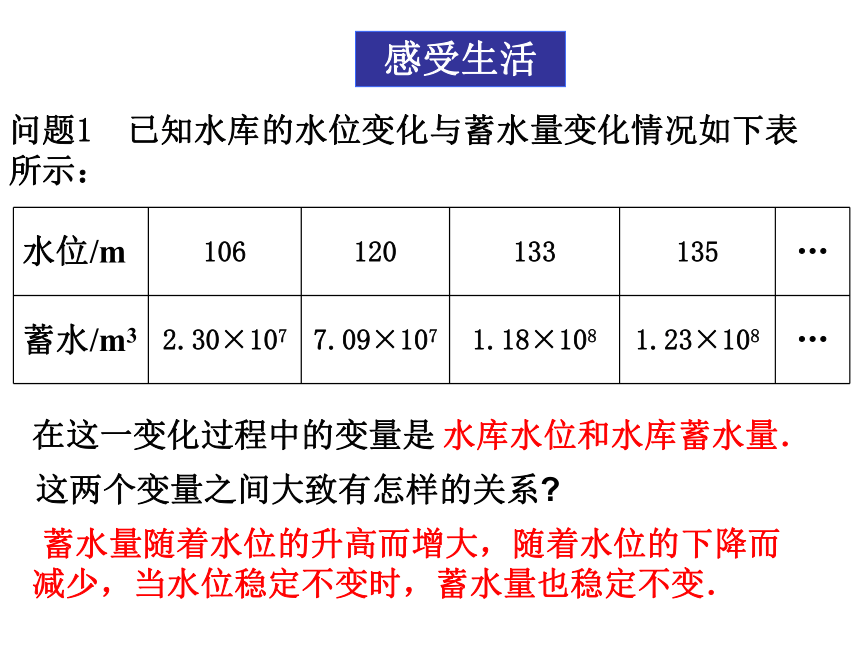
问题1 已知水库的水位变化与蓄水量变化情况如下表所示:
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
在这一变化过程中的变量是
这两个变量之间大致有怎样的关系?
水库水位和水库蓄水量.
蓄水量随着水位的升高而增大,随着水位的下降而减少,当水位稳定不变时,蓄水量也稳定不变.
感受生活
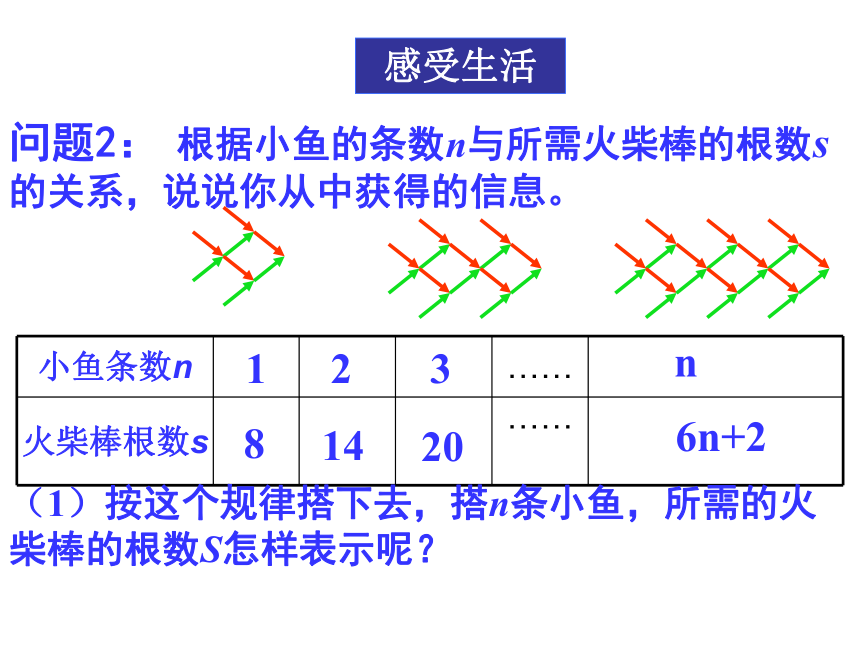
问题2: 根据小鱼的条数n与所需火柴棒的根数s的关系,说说你从中获得的信息。
小鱼条数n
……
火柴棒根数s
……
3
14
20
8
1
2
感受生活
(1)按这个规律搭下去,搭n条小鱼,所需的火柴棒的根数S怎样表示呢?
n
6n+2
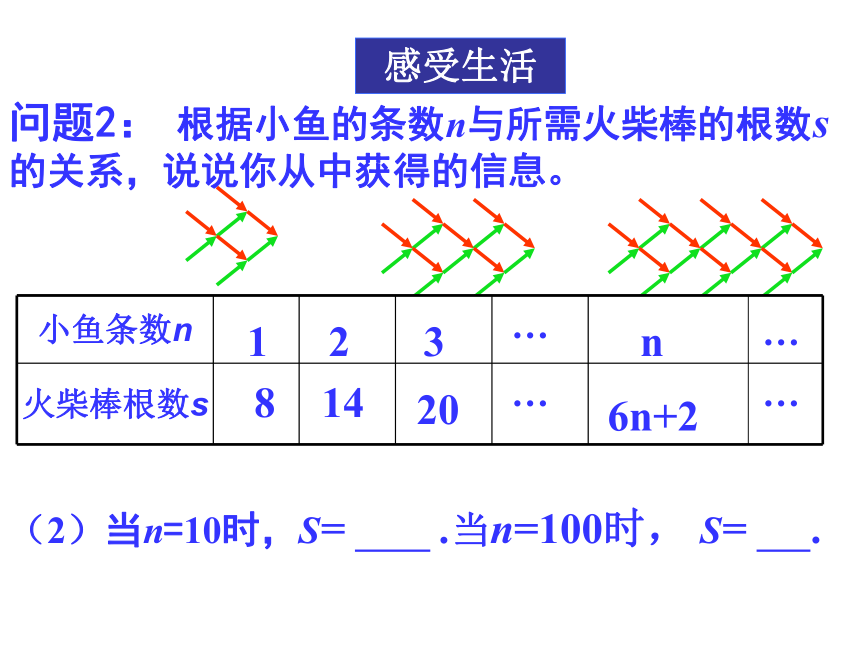
问题2: 根据小鱼的条数n与所需火柴棒的根数s的关系,说说你从中获得的信息。
小鱼条数n
火柴棒根数s
3
14
20
8
1
2
感受生活
(2)当n=10时,S= .当n=100时, S= .
n
6n+2
…
…
…
…
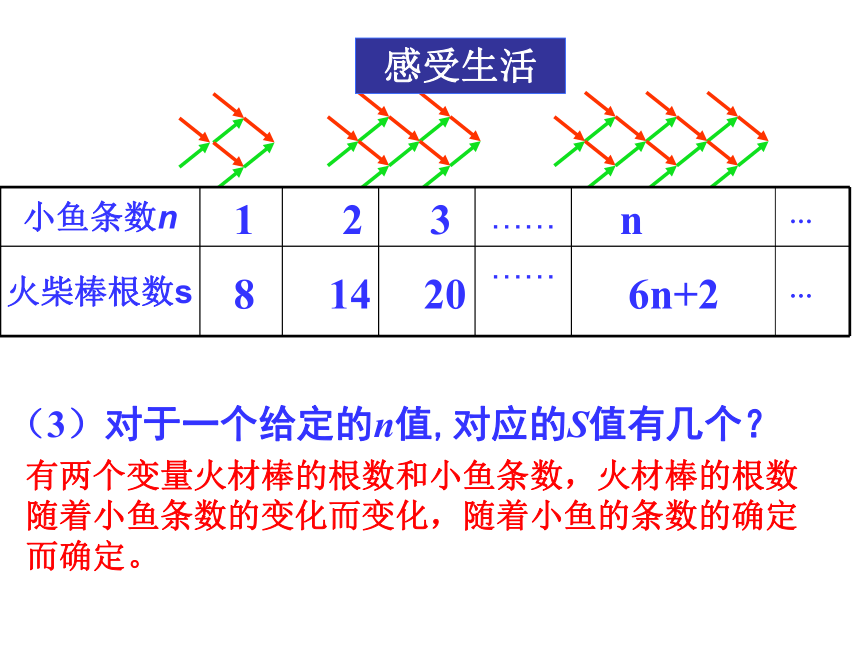
小鱼条数n
……
火柴棒根数s
……
n
3
14
20
8
1
2
8+6(n-1)
(3)对于一个给定的n值,对应的S值有几个?
感受生活
6n+2
…
…
有两个变量火材棒的根数和小鱼条数,火材棒的根数随着小鱼条数的变化而变化,随着小鱼的条数的确定而确定。
波纹圆的面积和半径.波纹圆的面积随着半径的变化而变化;随着半径的确定而确定.
(2)面积S与半径R的关系式是什么?
S= πR2
问题三:向平静的湖面投一石子,便会形成以落水点为圆心的一系列不断变化的圆。
(1)在这个变化过程中,有哪些变量?
感受生活
问题:上述问题有共同之处吗? 请同学们交流。
(都有几个变量?变量之间有什么关系)
合作交流
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
在上述例子中,每个变化过程中都存在着两个变量,当其中一个变量变化时,另一个变量也随着发生变化,当一个变量确定时,另一个变量也随着确定。
一般地,在一个变化的过程中有两个变量x和y.如果对于x的每一个值,y都有唯一的值与它对应,那么我们称y是x的函数(function),其中,x是自变量,y是因变量。
新知探索
合作交流
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
例如:水库蓄水量是水位的函数;
搭小鱼所需火柴的根数是所搭小鱼条数的函数
圆面积是半径的函数。
2、 在学习了函数的概念后,同学们试着自己举一些函数的实例:
小明:
圆的半径为r,面积S是半径r的函数,r是自变量.
你认为他们说的正确吗?为什么?
小亮:
长方体的长是a,宽是b,高是4,长方体的体积V是长a的函数.
练一练
②∣ y ∣ = x
x是y的函数吗?
3、下面变化关系中,y是x的函数吗?
①y-6x=1
练一练
例1.用一根2m长的铁丝围成一个长方形。
(1)当长方形的宽为0.1m时,长为 —— m
(2)当长方形的宽为0.2m时,长为 —— m
(3)当长方形的宽为 b m时,长为 —— m
0.9
0.8
(1-b)
(4)长方形的长a是宽b的函数吗?为什么?
链接生活
4、已知一个长方形的面积是长的5倍,若长为a,问:面积S与长a的关系?并指出其中常量、自变量、因变量,哪个是哪个的函数?
5、用总长为60m的篱笆围成一个矩形场地,求矩形的面积S与一边L 的关系?
6、“沙漏”是我国古代一种计量时间的仪器,它根据一个容器里的细沙漏到另一个容器中的数量来计算时间。请说出这个变化过程中的自变量,因变量。
心灵体验
时间是漏到另一容器中细沙的数量的函数
7、按图示的运算程序,输入一个实数x,便可以输出一个相应的实数y。y是x的函数吗?为什么?
输入x
输出y
+2
×5
-4
心灵体验
(1)
+2
×5
-4
输入x
输出y
(2)
输入x
( )2
输出y
(3)
输入x
输出y
7、按图示的运算程序,输入一个x的值,便可输出相应的y的值,y是x的函数吗?为什么?
判断两个变量是否具有函数关系以什么 为依据呢?
点评:
对于一个变量的每一个值,另一个变量都有唯一确定的值与之对应。
8、用60m的篱笆围成矩形,使矩形一边靠墙,另三边用篱笆围成
(1)写出矩形面积s(m2)与平行于墙的一边长a(m)的关系式,并指出关系式中的变量;
(2)写出矩形面积s(m2)与垂直于墙的一边长b(m)的关系式,并指出关系式中的自变量和函数。
墙
a
b
b
S=(60-2b)b
S=(30-0.5a) a
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
9、下图是气温自动记录仪记录的某地一天的气温变化曲线.
( 2 ) 图象中有几个变量?它们之间有怎样的关系?
(1)这天的6时 14时和14时的气温分别为多少?
气温T是时间t的函数?
心灵体验
反之时间t是气温T的函数吗?
你学到哪些知识?
1.四个概念
①常量与变量
②自变量与函数
2.判断两个变量具有函数关系的依据
一列动车从甲地驶往乙地,在16:17到16:22这个时段,列车以200千米/时的速度匀速行驶.在列车行驶过程中,哪些量没有变化?哪些量是在不断的变化?
在这一过程中,没有变化的量是:
列车行驶的速度不变;
从甲地到乙地的路程不变.
列车行驶的总时间不变
在这一过程中,变化了的量是:
列车行驶的时间在不断变化;
列车距离起点和终点的路程也在不断变化.
常量:
在某一变化过程中,数值保持不变的量叫做常量.
变量:
在某一变化过程中,可以取不同数值的量叫做变量.
1、下列各关系式中有常量和变量吗?
(1)直角三角形两锐角∠A ,∠B的关系式为∠A+∠B=900
(2)矩形的长a一定,面积s和宽b 的关系式为s = a b
(3)矩形的宽b一定,面积s和长a的关系式为s = a b
常量与变量不是绝对的,而是相对于一个变化过程而言的。
练一练
问题1 已知水库的水位变化与蓄水量变化情况如下表所示:
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
在这一变化过程中的变量是
这两个变量之间大致有怎样的关系?
水库水位和水库蓄水量.
蓄水量随着水位的升高而增大,随着水位的下降而减少,当水位稳定不变时,蓄水量也稳定不变.
感受生活
问题2: 根据小鱼的条数n与所需火柴棒的根数s的关系,说说你从中获得的信息。
小鱼条数n
……
火柴棒根数s
……
3
14
20
8
1
2
感受生活
(1)按这个规律搭下去,搭n条小鱼,所需的火柴棒的根数S怎样表示呢?
n
6n+2
问题2: 根据小鱼的条数n与所需火柴棒的根数s的关系,说说你从中获得的信息。
小鱼条数n
火柴棒根数s
3
14
20
8
1
2
感受生活
(2)当n=10时,S= .当n=100时, S= .
n
6n+2
…
…
…
…
小鱼条数n
……
火柴棒根数s
……
n
3
14
20
8
1
2
8+6(n-1)
(3)对于一个给定的n值,对应的S值有几个?
感受生活
6n+2
…
…
有两个变量火材棒的根数和小鱼条数,火材棒的根数随着小鱼条数的变化而变化,随着小鱼的条数的确定而确定。
波纹圆的面积和半径.波纹圆的面积随着半径的变化而变化;随着半径的确定而确定.
(2)面积S与半径R的关系式是什么?
S= πR2
问题三:向平静的湖面投一石子,便会形成以落水点为圆心的一系列不断变化的圆。
(1)在这个变化过程中,有哪些变量?
感受生活
问题:上述问题有共同之处吗? 请同学们交流。
(都有几个变量?变量之间有什么关系)
合作交流
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
在上述例子中,每个变化过程中都存在着两个变量,当其中一个变量变化时,另一个变量也随着发生变化,当一个变量确定时,另一个变量也随着确定。
一般地,在一个变化的过程中有两个变量x和y.如果对于x的每一个值,y都有唯一的值与它对应,那么我们称y是x的函数(function),其中,x是自变量,y是因变量。
新知探索
合作交流
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
例如:水库蓄水量是水位的函数;
搭小鱼所需火柴的根数是所搭小鱼条数的函数
圆面积是半径的函数。
2、 在学习了函数的概念后,同学们试着自己举一些函数的实例:
小明:
圆的半径为r,面积S是半径r的函数,r是自变量.
你认为他们说的正确吗?为什么?
小亮:
长方体的长是a,宽是b,高是4,长方体的体积V是长a的函数.
练一练
②∣ y ∣ = x
x是y的函数吗?
3、下面变化关系中,y是x的函数吗?
①y-6x=1
练一练
例1.用一根2m长的铁丝围成一个长方形。
(1)当长方形的宽为0.1m时,长为 —— m
(2)当长方形的宽为0.2m时,长为 —— m
(3)当长方形的宽为 b m时,长为 —— m
0.9
0.8
(1-b)
(4)长方形的长a是宽b的函数吗?为什么?
链接生活
4、已知一个长方形的面积是长的5倍,若长为a,问:面积S与长a的关系?并指出其中常量、自变量、因变量,哪个是哪个的函数?
5、用总长为60m的篱笆围成一个矩形场地,求矩形的面积S与一边L 的关系?
6、“沙漏”是我国古代一种计量时间的仪器,它根据一个容器里的细沙漏到另一个容器中的数量来计算时间。请说出这个变化过程中的自变量,因变量。
心灵体验
时间是漏到另一容器中细沙的数量的函数
7、按图示的运算程序,输入一个实数x,便可以输出一个相应的实数y。y是x的函数吗?为什么?
输入x
输出y
+2
×5
-4
心灵体验
(1)
+2
×5
-4
输入x
输出y
(2)
输入x
( )2
输出y
(3)
输入x
输出y
7、按图示的运算程序,输入一个x的值,便可输出相应的y的值,y是x的函数吗?为什么?
判断两个变量是否具有函数关系以什么 为依据呢?
点评:
对于一个变量的每一个值,另一个变量都有唯一确定的值与之对应。
8、用60m的篱笆围成矩形,使矩形一边靠墙,另三边用篱笆围成
(1)写出矩形面积s(m2)与平行于墙的一边长a(m)的关系式,并指出关系式中的变量;
(2)写出矩形面积s(m2)与垂直于墙的一边长b(m)的关系式,并指出关系式中的自变量和函数。
墙
a
b
b
S=(60-2b)b
S=(30-0.5a) a
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T(?C)
2
4
6
8
-2
-4
0
9、下图是气温自动记录仪记录的某地一天的气温变化曲线.
( 2 ) 图象中有几个变量?它们之间有怎样的关系?
(1)这天的6时 14时和14时的气温分别为多少?
气温T是时间t的函数?
心灵体验
反之时间t是气温T的函数吗?
你学到哪些知识?
1.四个概念
①常量与变量
②自变量与函数
2.判断两个变量具有函数关系的依据
