人教版八年级数学下册课件:19.2.2一次函数的图象与性质(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.2.2一次函数的图象与性质(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
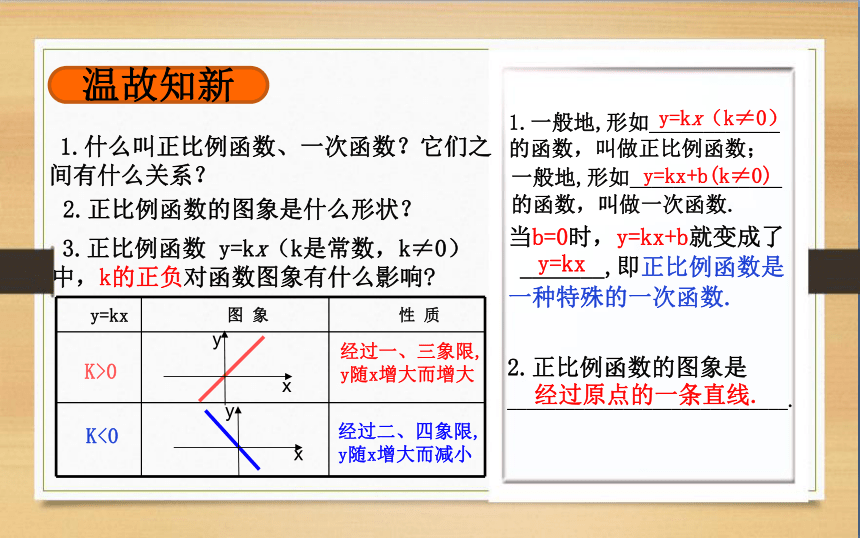
1.什么叫正比例函数、一次函数?它们之间有什么关系?
1.一般地,形如____________ 的函数,叫做正比例函数;
一般地,形如______________ 的函数,叫做一次函数.
当b=0时,y=kx+b就变成了
_______,即正比例函数是一种特殊的一次函数.
2.正比例函数的图象是什么形状?
2.正比例函数的图象是_____________________________.
y=kx(k≠0)
y=kx+b(k≠0)
y=kx
经过原点的一条直线.
3.正比例函数 y=kx(k是常数,k≠0)中,k的正负对函数图象有什么影响
y=kx 图 象 性 质
K>0
y
x
经过一、三象限,
y随x增大而增大
K<0
y
x
经过二、四象限,
y随x增大而减小
温故知新
既然正比例函数是特殊的一次函数, 正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗? 它们图象之间有什么关系 一次函数又有什么性质呢
19.2.2 一次函数
第2课时 一次函数的图象和性质
学习目标
1
2
3
会选择两个合适的点画出一次函数的图象.
掌握一次函数的图象和性质与k,b的关系.
知道正比例函数与一次函数的图象之间的平移关系.
活动1:画函数图象
在同一坐标系中画出下列函数的图象:
(每小组选做一题)
(1)y=-3x y=-3x+4
(2)y=x y=x+1
(3)y=-2x y=-2x-1
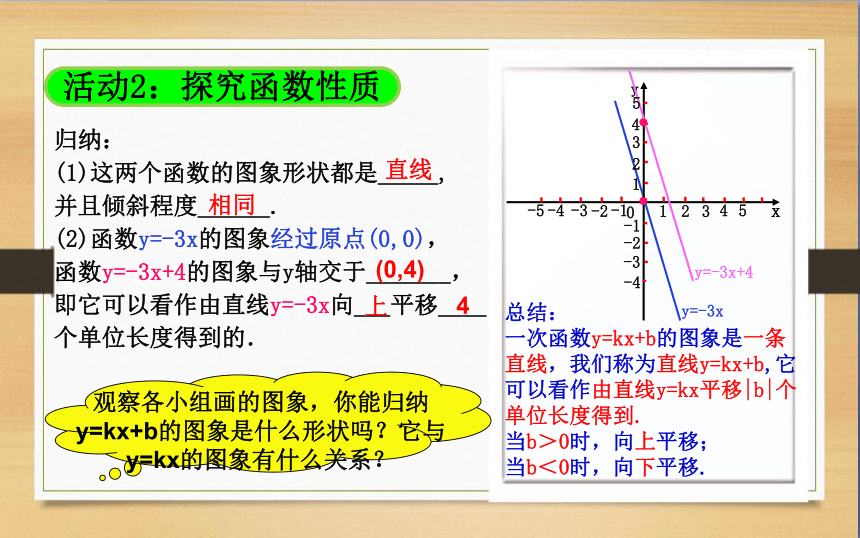
归纳:
(1)这两个函数的图象形状都是_____, 并且倾斜程度______.
(2)函数y=-3x的图象经过原点(0,0), 函数y=-3x+4的图象与y轴交于_______,即它可以看作由直线y=-3x向___平移____个单位长度得到的.
0
-4
y
x
y=-3x+4
1
2
3
5
4
-5
-3
-2
-1
1
2
3
4
5
-1
-2
-3
-4
y=-3x
观察各小组画的图象,你能归纳y=kx+b的图象是什么形状吗?它与y=kx的图象有什么关系?
活动2:探究函数性质
总结: 一次函数y=kx+b的图象是一条 直线,我们称为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到. 当b>0时,向上平移; 当b<0时,向下平移.
直线
相同
(0,4)
上
4
活动3:再画函数图象
例3:画出函数y=x-1与y=-2x+1的图象.
解法一: 平移法
(1)先画________,再向__平移__个单位.
直线y=x
下
1
(2)先画__________,再向__平移__个单位.
直线y=-2x
上
1
解法二: 两点法
x 0
y=x-1
-1
0
怎样画一次函数图象更简单呢
1
x 0
y=-2x+1
1
0
0.5
总结:
画一次函数的图象时,只要描出合适关系式的两点,再连接两点即可,我们通常选取(0,b)和(- ,0 )这两个点,也就是选取图象与x轴和y轴的交点坐标.
活动4:再探函数性质
思考: 观察这两个函数的图象, 类比正比例函数y=kx(k≠0,k为常数)的增减性,探究一次函数y=kx+b (k≠0,k、b为常数)的 增减性.
一次函数的性质:
当k>0时,直线从左向右上升, y随x的增大而增大;
当k<0时,直线从左向右下降,y随x的增大而减小.
结论:
b决定直线y=kx+b与y轴交点的坐标(0,b).
一次函数的性质:
当k>0时,直线从左向右上升, y随x的增大而增大;
当k<0时,直线从左向右下降,y随x的增大而减小.
1
2
3
4
5
6
4
课堂检测
1
下列函数中,y的值随x值的增大而增大
的函数是____.
A.y=-2x B.y=-2x+1
C.y=5x-2 D.y=-x-2
C
2
一次函数y=-x-2的图象大致是 ( )
A
B
C
D
D
3
3.(1)直线y=4x-3是由直线______向___平移____个长度单位而得到.
(2)将直线y=x-5向上平移5个单位,得到直线为____________.
y=4x
下
3
y=x
4
函数y=2x-4与y轴的交点为_______,
与x轴交于______,图象经过________象限,
y随x的增大而_______.
(0,-4)
(2,0)
一、三、四
增大
5
时间是一个“常数”,但对勤奋者来说是一个“变数”,你在学习上的收获与你平时的付出是成正比的。
6
用你认为最简单的方法画出下列函数的图象:
y = 5x-2;
课堂小结
一次函数y=kx+b的图象是一条直线,与y=kx的图象平行,可以看作由直线y=kx平移|b|个单位长度得到.
一次函数图象的画法:
①平移法;②两点法
通过今天的学习, 用你自己的话说说你的收获和体会.
一次函数的性质:
当k>0时,直线从左向右上升, y随x的增大而增大;
当k<0时,直线从左向右下降,y随x的增大而减小.
布置作业
1.阅读作业:复习课本内容,整理笔记.
2.家庭作业:
(1)课本第99页习题19.2第4、5题;
(2)填写《配套练习》中相关练习题.
谢谢!
1.什么叫正比例函数、一次函数?它们之间有什么关系?
1.一般地,形如____________ 的函数,叫做正比例函数;
一般地,形如______________ 的函数,叫做一次函数.
当b=0时,y=kx+b就变成了
_______,即正比例函数是一种特殊的一次函数.
2.正比例函数的图象是什么形状?
2.正比例函数的图象是_____________________________.
y=kx(k≠0)
y=kx+b(k≠0)
y=kx
经过原点的一条直线.
3.正比例函数 y=kx(k是常数,k≠0)中,k的正负对函数图象有什么影响
y=kx 图 象 性 质
K>0
y
x
经过一、三象限,
y随x增大而增大
K<0
y
x
经过二、四象限,
y随x增大而减小
温故知新
既然正比例函数是特殊的一次函数, 正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗? 它们图象之间有什么关系 一次函数又有什么性质呢
19.2.2 一次函数
第2课时 一次函数的图象和性质
学习目标
1
2
3
会选择两个合适的点画出一次函数的图象.
掌握一次函数的图象和性质与k,b的关系.
知道正比例函数与一次函数的图象之间的平移关系.
活动1:画函数图象
在同一坐标系中画出下列函数的图象:
(每小组选做一题)
(1)y=-3x y=-3x+4
(2)y=x y=x+1
(3)y=-2x y=-2x-1
归纳:
(1)这两个函数的图象形状都是_____, 并且倾斜程度______.
(2)函数y=-3x的图象经过原点(0,0), 函数y=-3x+4的图象与y轴交于_______,即它可以看作由直线y=-3x向___平移____个单位长度得到的.
0
-4
y
x
y=-3x+4
1
2
3
5
4
-5
-3
-2
-1
1
2
3
4
5
-1
-2
-3
-4
y=-3x
观察各小组画的图象,你能归纳y=kx+b的图象是什么形状吗?它与y=kx的图象有什么关系?
活动2:探究函数性质
总结: 一次函数y=kx+b的图象是一条 直线,我们称为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到. 当b>0时,向上平移; 当b<0时,向下平移.
直线
相同
(0,4)
上
4
活动3:再画函数图象
例3:画出函数y=x-1与y=-2x+1的图象.
解法一: 平移法
(1)先画________,再向__平移__个单位.
直线y=x
下
1
(2)先画__________,再向__平移__个单位.
直线y=-2x
上
1
解法二: 两点法
x 0
y=x-1
-1
0
怎样画一次函数图象更简单呢
1
x 0
y=-2x+1
1
0
0.5
总结:
画一次函数的图象时,只要描出合适关系式的两点,再连接两点即可,我们通常选取(0,b)和(- ,0 )这两个点,也就是选取图象与x轴和y轴的交点坐标.
活动4:再探函数性质
思考: 观察这两个函数的图象, 类比正比例函数y=kx(k≠0,k为常数)的增减性,探究一次函数y=kx+b (k≠0,k、b为常数)的 增减性.
一次函数的性质:
当k>0时,直线从左向右上升, y随x的增大而增大;
当k<0时,直线从左向右下降,y随x的增大而减小.
结论:
b决定直线y=kx+b与y轴交点的坐标(0,b).
一次函数的性质:
当k>0时,直线从左向右上升, y随x的增大而增大;
当k<0时,直线从左向右下降,y随x的增大而减小.
1
2
3
4
5
6
4
课堂检测
1
下列函数中,y的值随x值的增大而增大
的函数是____.
A.y=-2x B.y=-2x+1
C.y=5x-2 D.y=-x-2
C
2
一次函数y=-x-2的图象大致是 ( )
A
B
C
D
D
3
3.(1)直线y=4x-3是由直线______向___平移____个长度单位而得到.
(2)将直线y=x-5向上平移5个单位,得到直线为____________.
y=4x
下
3
y=x
4
函数y=2x-4与y轴的交点为_______,
与x轴交于______,图象经过________象限,
y随x的增大而_______.
(0,-4)
(2,0)
一、三、四
增大
5
时间是一个“常数”,但对勤奋者来说是一个“变数”,你在学习上的收获与你平时的付出是成正比的。
6
用你认为最简单的方法画出下列函数的图象:
y = 5x-2;
课堂小结
一次函数y=kx+b的图象是一条直线,与y=kx的图象平行,可以看作由直线y=kx平移|b|个单位长度得到.
一次函数图象的画法:
①平移法;②两点法
通过今天的学习, 用你自己的话说说你的收获和体会.
一次函数的性质:
当k>0时,直线从左向右上升, y随x的增大而增大;
当k<0时,直线从左向右下降,y随x的增大而减小.
布置作业
1.阅读作业:复习课本内容,整理笔记.
2.家庭作业:
(1)课本第99页习题19.2第4、5题;
(2)填写《配套练习》中相关练习题.
谢谢!
