人教版八年级下册17.1探索勾股定理证明课件(共33张PPT)
文档属性
| 名称 | 人教版八年级下册17.1探索勾股定理证明课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 16:50:43 | ||
图片预览





文档简介
无字证明
国际调查组报告
约公元前500年,毕达哥拉斯学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线的长度是不可公度的.按照毕达哥拉斯定理(勾股定理),若正方形边长是1,则对角线的长不是一个有理数,它不能表示成两个整数之比,这一事实不但与毕氏学派的哲学信念大相径庭,而且建立在任何线段都可公度基础上的几何学面临被推翻的威胁,第一次数学危机由此爆发。据说,毕达哥拉斯学派对希帕索斯的发现十分惶恐、恼怒,为了保守秘密,最后将希帕索斯投入大海。
不能表示成两个整数之比的数,15世纪意大利著名画家达.芬奇称之为“无理的数”,无理数的英文“irrational”原义就是“不可比”。第一次数学危机一直持续到19世纪实数的基础建立以后才圆满解决。我们将在下一章学习有关实数的知识 。
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
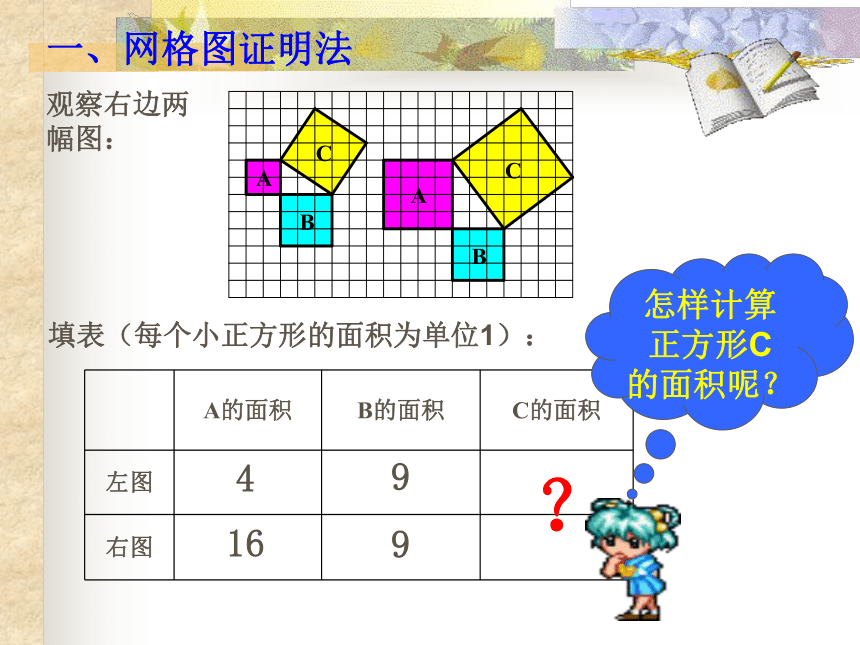
探索勾股定理
b
a
c
a2+b2=c2
即直角三角形两直角边的平方和等于斜边的平方.
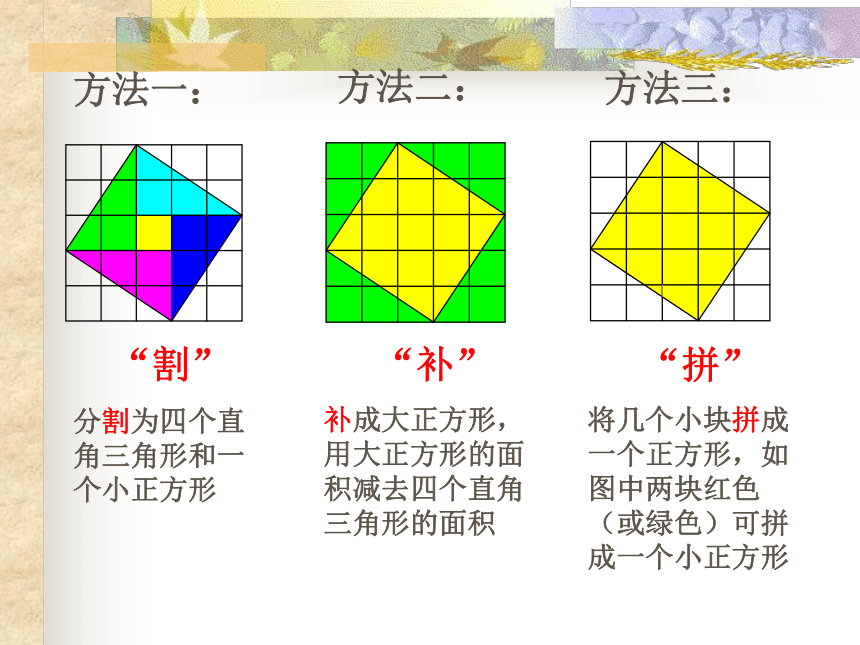
一、网格图证明法
观察右边两幅图:
填表(每个小正方形的面积为单位1):
右图
左图
C的面积
B的面积
A的面积
4
?
怎样计算正方形C的面积呢?
9
16
9
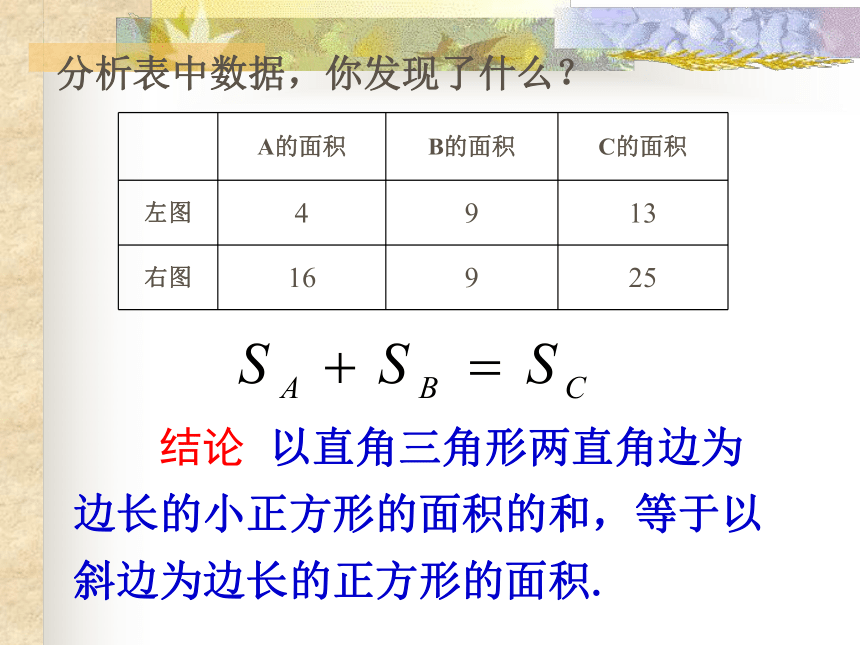
“割”
“补”
“拼”
方法一:
方法二:
方法三:
分割为四个直角三角形和一个小正方形
补成大正方形,用大正方形的面积减去四个直角三角形的面积
将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形
分析表中数据,你发现了什么?
25
9
16
右图
13
9
4
左图
C的面积
B的面积
A的面积
结论 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
C
A
B
A
B
C
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
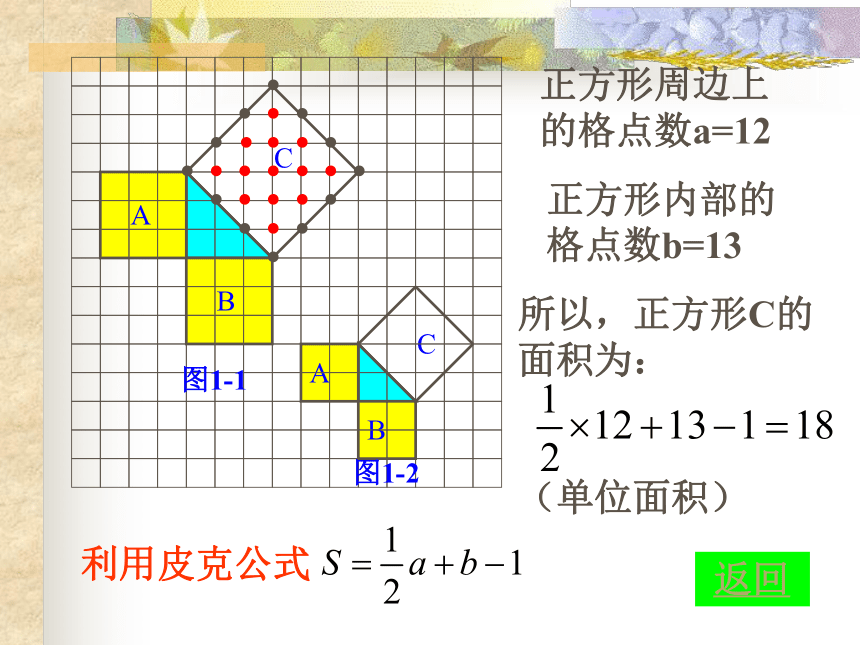
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
(单位面积)
返回
图1-1
图1-2
二、拼图法
c
a
b
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);
2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c的正方形?
4、你能否就你拼出的图说明a2+b2=c2?
c
a
b
c
a
b
c
a
b
c
a
b
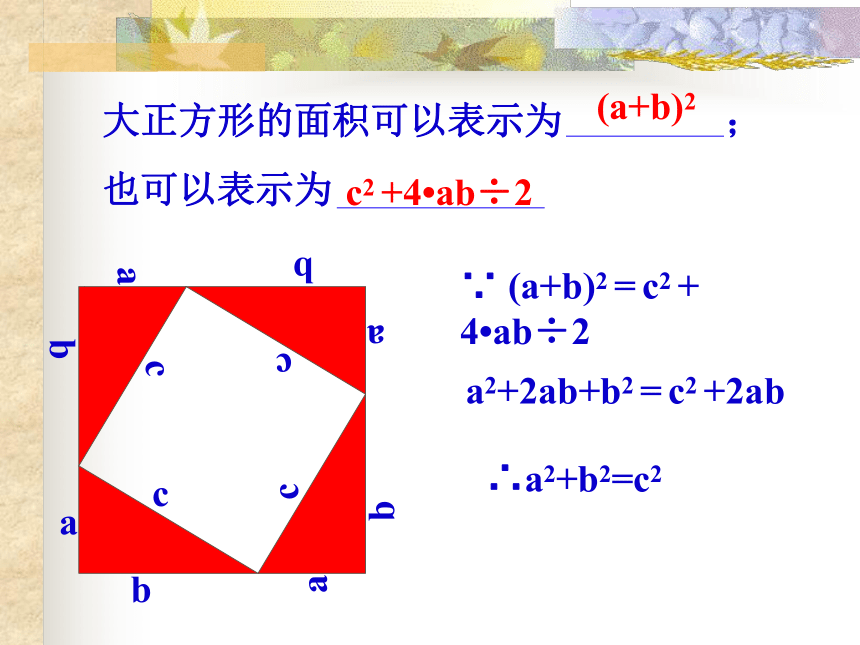
∵ (a+b)2 = c2 + 4?ab÷2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab÷2
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4?ab÷2 +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab÷2-(b- a)2
a
a
b
b
c
c
三、“总统证法”.
美国第二十任总统伽菲尔德的证法
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
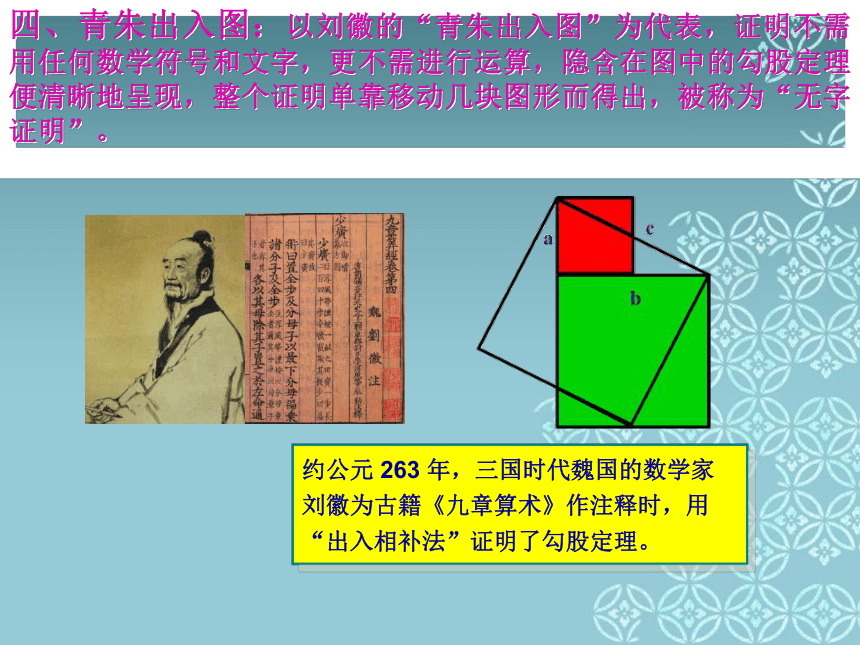
四、青朱出入图:以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
约公元 263 年,三国时代魏国的数学家刘徽为古籍《九章算术》作注释时,用“出入相补法”证明了勾股定理。
a
b
c
①
②
③
④
⑤
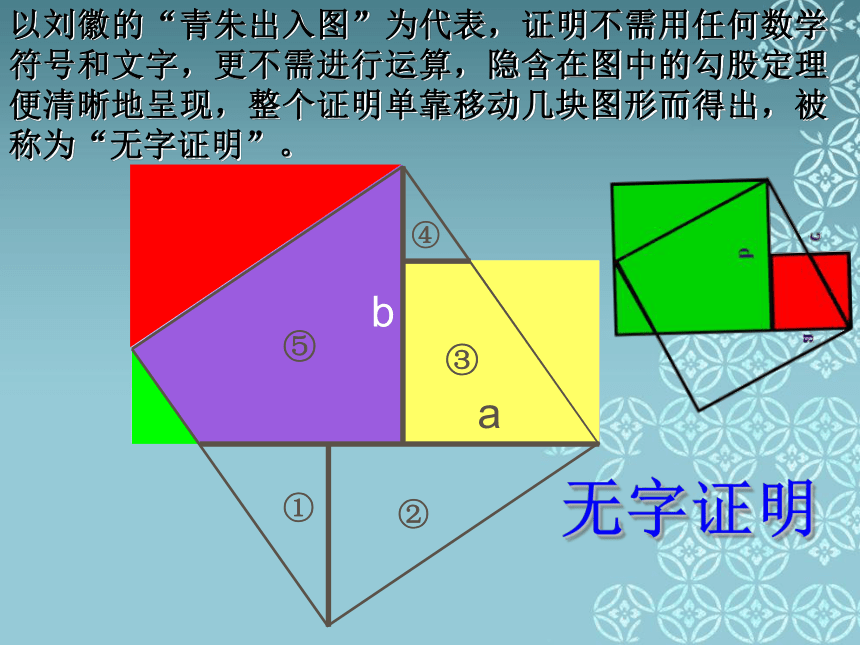
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
做法是将一条垂直线和一条水平线,将较大直角边的正方形分成 4 分。之后依照图中的颜色,将两个直角边的正方形填入斜边正方形之中,便可完成定理的证明。
单击图片打开
五、在印度、在阿拉伯世界和欧洲出现的一种拼图证明
a
b
c
A
B
C
D
E
F
O
意大利文艺复兴时代的著名画家达·芬奇对勾股定理进行了研究。
六:达·芬奇证法
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
勾股定理与第一次数学危机
1
1
?
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
D
A
B
C
蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
只要求答案
议一议:用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2?
a
a
b
b
c
c
3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
16-X
x
D
A
B
C
解:设这个三角形为ABC,高为AD,设AB为X,则BC为(32-2X),BD是(16-x)
由勾股定理得:
X2=(16-X)2 +82
即X2=256-32X+X2 +64
∴ X=10
∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48
试一试
有一个水池,水面是一个边长为10尺的正方形,在
水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根
芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池
的深度和这根芦苇的长度各是多少?
5尺
1尺
x 尺
x2 + 52 = (x+1)2
x = 12
水池
补充:如图,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
(3)如图在△ABC中,∠ACB=90?, CD⊥AB,D为垂足,AC=2.1cm,BC=2.8cm.
求① △ABC的面积;
②斜边AB的长;
③斜边AB上的高CD的长。
D
A
B
C
欣赏有趣的图形:
1
1
毕达哥拉斯树
螺形图
补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
C
D
2. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC是( )
(A)直角三角形 (B)锐角三角形
(C)钝角三角形 (D)以上答案都不对
3. 在△ABC中,AB=13,AC=20,高AD=12,
则BC的长为————————————————
C
A
20
B
13
D
┓
12
16
5
A
C
20
B
13
D
┓
12
5
16
21或11
如果电梯的长、宽、高分别是1.5、1.5、2.2米,那么能放入电梯内的竹竿的最大长度大约是多少?你能估计出小明买的竹竿至少是多少米吗?
2、如图有两颗树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到
另一棵树的树梢,至少飞了多少米?
8m
2m
8m
A
B
C
D
E
1.如图,两个正方形的面积分别为64,49,则AC=( )
A
D
C
64
49
2.由四根木棒,长度分别为3,4,5,6
若去其中三根木棒组呈三角形,有( )
中取法,其中,能构成直角三角形的是( )
? 说一说 ?
2.假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,
在折向北走到6千米处往东一拐,
仅走1千米就找到宝藏,问登陆点A
到宝藏埋藏点B的距离是多少千米?
8
A
B
2
3
6
1
C
5.如图,长方体的长为15 cm,宽为
10 cm,高为20 cm,点B离点C 5 cm,
一只蚂蚁如果要沿着长方体的表面从点
A爬到点B,需要爬行的最短距离是多少?
?
?
?
?
8.如图,四边形ABCD中,∠B=∠D=90°,
∠C=45°,AD=1,BC=2,求CD的长.
A
B
C
D
E
无字证明
国际调查组报告
约公元前500年,毕达哥拉斯学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线的长度是不可公度的.按照毕达哥拉斯定理(勾股定理),若正方形边长是1,则对角线的长不是一个有理数,它不能表示成两个整数之比,这一事实不但与毕氏学派的哲学信念大相径庭,而且建立在任何线段都可公度基础上的几何学面临被推翻的威胁,第一次数学危机由此爆发。据说,毕达哥拉斯学派对希帕索斯的发现十分惶恐、恼怒,为了保守秘密,最后将希帕索斯投入大海。
不能表示成两个整数之比的数,15世纪意大利著名画家达.芬奇称之为“无理的数”,无理数的英文“irrational”原义就是“不可比”。第一次数学危机一直持续到19世纪实数的基础建立以后才圆满解决。我们将在下一章学习有关实数的知识 。
a
b
c
①
②
③
④
⑤
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
2、如图有两颗树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到
另一棵树的树梢,至少飞了多少米?
8m
2m
8m
A
B
C
D
E
国际调查组报告
约公元前500年,毕达哥拉斯学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线的长度是不可公度的.按照毕达哥拉斯定理(勾股定理),若正方形边长是1,则对角线的长不是一个有理数,它不能表示成两个整数之比,这一事实不但与毕氏学派的哲学信念大相径庭,而且建立在任何线段都可公度基础上的几何学面临被推翻的威胁,第一次数学危机由此爆发。据说,毕达哥拉斯学派对希帕索斯的发现十分惶恐、恼怒,为了保守秘密,最后将希帕索斯投入大海。
不能表示成两个整数之比的数,15世纪意大利著名画家达.芬奇称之为“无理的数”,无理数的英文“irrational”原义就是“不可比”。第一次数学危机一直持续到19世纪实数的基础建立以后才圆满解决。我们将在下一章学习有关实数的知识 。
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
探索勾股定理
b
a
c
a2+b2=c2
即直角三角形两直角边的平方和等于斜边的平方.
一、网格图证明法
观察右边两幅图:
填表(每个小正方形的面积为单位1):
右图
左图
C的面积
B的面积
A的面积
4
?
怎样计算正方形C的面积呢?
9
16
9
“割”
“补”
“拼”
方法一:
方法二:
方法三:
分割为四个直角三角形和一个小正方形
补成大正方形,用大正方形的面积减去四个直角三角形的面积
将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形
分析表中数据,你发现了什么?
25
9
16
右图
13
9
4
左图
C的面积
B的面积
A的面积
结论 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
C
A
B
A
B
C
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
(单位面积)
返回
图1-1
图1-2
二、拼图法
c
a
b
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);
2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c的正方形?
4、你能否就你拼出的图说明a2+b2=c2?
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4?ab÷2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab÷2
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2= 4?ab÷2 +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab÷2-(b- a)2
a
a
b
b
c
c
三、“总统证法”.
美国第二十任总统伽菲尔德的证法
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
四、青朱出入图:以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
约公元 263 年,三国时代魏国的数学家刘徽为古籍《九章算术》作注释时,用“出入相补法”证明了勾股定理。
a
b
c
①
②
③
④
⑤
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
做法是将一条垂直线和一条水平线,将较大直角边的正方形分成 4 分。之后依照图中的颜色,将两个直角边的正方形填入斜边正方形之中,便可完成定理的证明。
单击图片打开
五、在印度、在阿拉伯世界和欧洲出现的一种拼图证明
a
b
c
A
B
C
D
E
F
O
意大利文艺复兴时代的著名画家达·芬奇对勾股定理进行了研究。
六:达·芬奇证法
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
勾股定理与第一次数学危机
1
1
?
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
D
A
B
C
蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
只要求答案
议一议:用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2?
a
a
b
b
c
c
3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
16-X
x
D
A
B
C
解:设这个三角形为ABC,高为AD,设AB为X,则BC为(32-2X),BD是(16-x)
由勾股定理得:
X2=(16-X)2 +82
即X2=256-32X+X2 +64
∴ X=10
∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48
试一试
有一个水池,水面是一个边长为10尺的正方形,在
水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根
芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池
的深度和这根芦苇的长度各是多少?
5尺
1尺
x 尺
x2 + 52 = (x+1)2
x = 12
水池
补充:如图,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
(3)如图在△ABC中,∠ACB=90?, CD⊥AB,D为垂足,AC=2.1cm,BC=2.8cm.
求① △ABC的面积;
②斜边AB的长;
③斜边AB上的高CD的长。
D
A
B
C
欣赏有趣的图形:
1
1
毕达哥拉斯树
螺形图
补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
C
D
2. 如图,正方形网格中的△ABC,若小方格边长为1,则△ABC是( )
(A)直角三角形 (B)锐角三角形
(C)钝角三角形 (D)以上答案都不对
3. 在△ABC中,AB=13,AC=20,高AD=12,
则BC的长为————————————————
C
A
20
B
13
D
┓
12
16
5
A
C
20
B
13
D
┓
12
5
16
21或11
如果电梯的长、宽、高分别是1.5、1.5、2.2米,那么能放入电梯内的竹竿的最大长度大约是多少?你能估计出小明买的竹竿至少是多少米吗?
2、如图有两颗树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到
另一棵树的树梢,至少飞了多少米?
8m
2m
8m
A
B
C
D
E
1.如图,两个正方形的面积分别为64,49,则AC=( )
A
D
C
64
49
2.由四根木棒,长度分别为3,4,5,6
若去其中三根木棒组呈三角形,有( )
中取法,其中,能构成直角三角形的是( )
? 说一说 ?
2.假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,
在折向北走到6千米处往东一拐,
仅走1千米就找到宝藏,问登陆点A
到宝藏埋藏点B的距离是多少千米?
8
A
B
2
3
6
1
C
5.如图,长方体的长为15 cm,宽为
10 cm,高为20 cm,点B离点C 5 cm,
一只蚂蚁如果要沿着长方体的表面从点
A爬到点B,需要爬行的最短距离是多少?
?
?
?
?
8.如图,四边形ABCD中,∠B=∠D=90°,
∠C=45°,AD=1,BC=2,求CD的长.
A
B
C
D
E
无字证明
国际调查组报告
约公元前500年,毕达哥拉斯学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线的长度是不可公度的.按照毕达哥拉斯定理(勾股定理),若正方形边长是1,则对角线的长不是一个有理数,它不能表示成两个整数之比,这一事实不但与毕氏学派的哲学信念大相径庭,而且建立在任何线段都可公度基础上的几何学面临被推翻的威胁,第一次数学危机由此爆发。据说,毕达哥拉斯学派对希帕索斯的发现十分惶恐、恼怒,为了保守秘密,最后将希帕索斯投入大海。
不能表示成两个整数之比的数,15世纪意大利著名画家达.芬奇称之为“无理的数”,无理数的英文“irrational”原义就是“不可比”。第一次数学危机一直持续到19世纪实数的基础建立以后才圆满解决。我们将在下一章学习有关实数的知识 。
a
b
c
①
②
③
④
⑤
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
2、如图有两颗树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到
另一棵树的树梢,至少飞了多少米?
8m
2m
8m
A
B
C
D
E
