人教版七年级数学下册第9章第1节第2部分不等式的性质 (4)(共31张PPT)
文档属性
| 名称 | 人教版七年级数学下册第9章第1节第2部分不等式的性质 (4)(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 16:51:30 | ||
图片预览







文档简介
9.1.2 不等式的性质
如果a=b, 能否得到a+2=b+2 ?
如果a=b, 能否得到0.5a=0.5b ?
如果a=b, 能否得到-2a= -2b ?
如果a=b, 能否得到a-2=b-2 ?
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
(1)5>3, 5+2___3+2 , 5-2___3-2 ;
(2)-1<3, -1+2___3+2 , -1-3___3-3 ;
根据发现的规律填空:当不等式两边加或减同一个数(正数
或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
用“﹥”或“﹤”填空,并总结其中的规律:
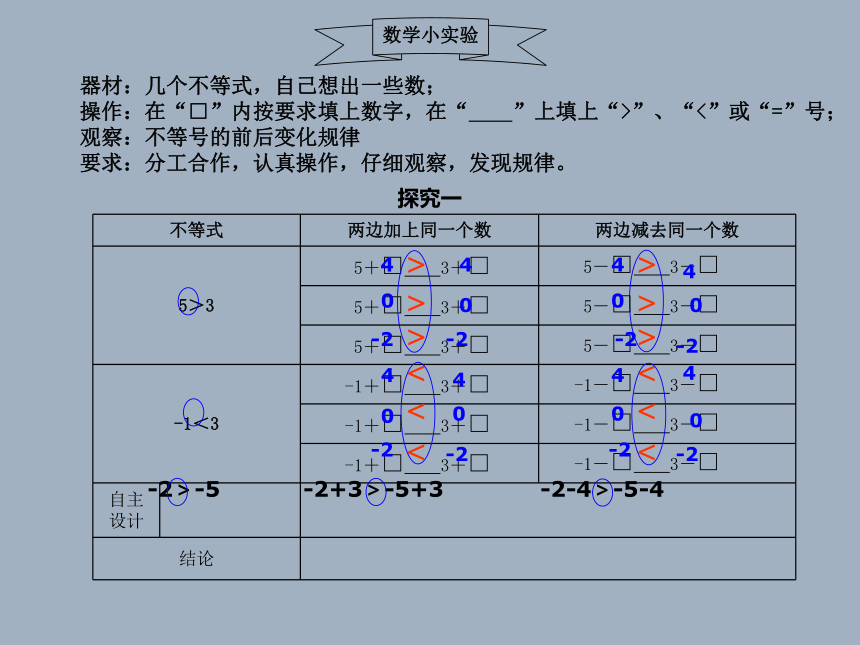
数学小实验
器材:几个不等式,自己想出一些数;
操作:在“□”内按要求填上数字,在“ ”上填上“>”、“<”或“=”号;
观察:不等号的前后变化规律
要求:分工合作,认真操作,仔细观察,发现规律。
不等式
两边加上同一个数
两边减去同一个数
5>3
5+□ 3+□
5-□ 3-□
5+□ 3+□
5-□ 3-□
5+□ 3+□
5-□ 3-□
-1<3
-1+□ 3+□
-1-□ 3-□
-1+□ 3+□
-1-□ 3-□
-1+□ 3+□
-1-□ 3-□
自主设计
结论
探究一
4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
>
>
>
>
>
>
<
<
<
<
<
<
-2>-5
-2+3>-5+3
-2-4>-5-4
+ C
-C
(或________)
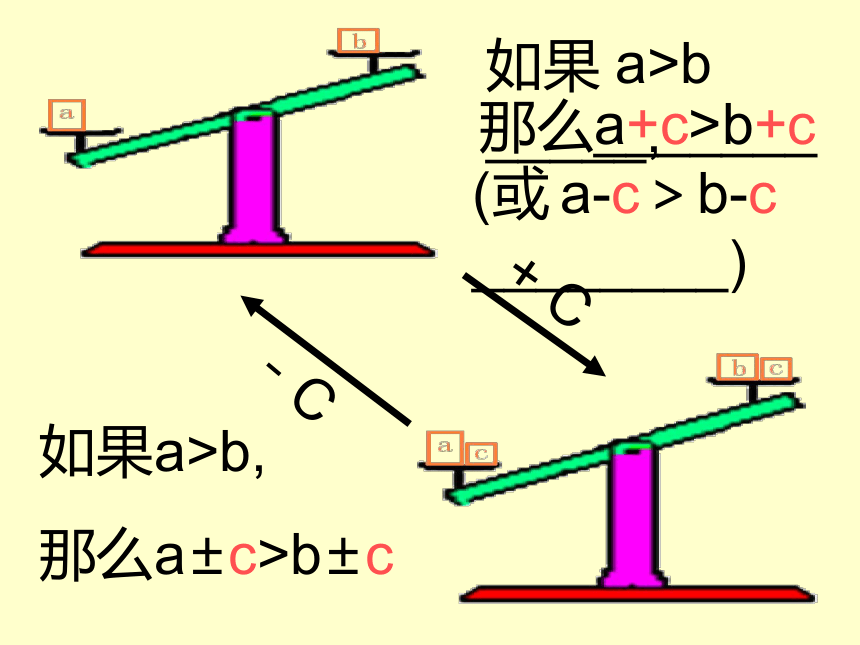
如果_____,
那么_______
如果a>b,
那么a±c>b±c
a>b
a+c>b+c
a-c>b-c
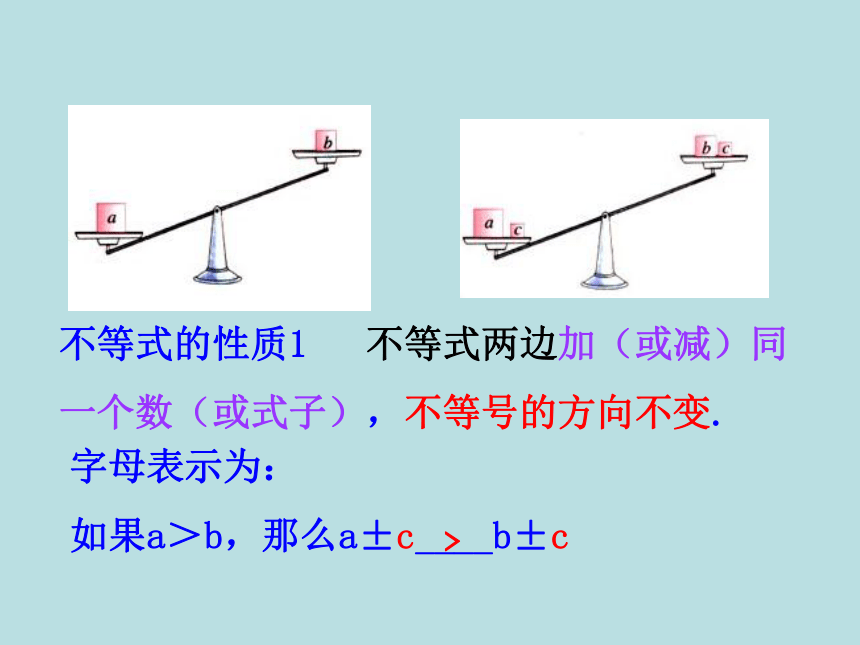
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
字母表示为:
如果a>b,那么a±c____b±c
﹥
(3) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4)–2<3, (-2)×6___3×6 , (-2) ×(-6)___3×(-6 )
当不等式两边乘同一个正数时,不等号的方向_____;
不变
而乘同一个负数时,不等号的方向_____;
改变
﹥
﹤
﹤
﹥
不等式还有什么类似的性质呢?
不等式
两边加上同一个数
两边减去同一个数
6>2
6×□ 2×□
6÷□ 2÷□
6×□ 2×□
6÷□ 2÷□
6×□ 2×□
6÷□ 2÷□
6×□ 2×□
6÷□ 2÷□
-2<3
-2×□ 3×□
-2÷□ 3÷□
-2×□ 3×□
-2÷□ 3÷□
-2×□ 3×□
-2÷□ 3÷□
-2×□ 3×□
-2÷□ 3÷□
自主设计
结论
探究二
数学小实验
器材:几个不等式,自己想出一些数;
操作:在“□”内按要求填上数字,在“ ”上填上“>”、“<”或“=”号;
观察:不等号的前后变化规律
要求:分工合作,认真操作,仔细观察,发现规律。
2
2
4
4
0
-4
>
<
0
-4
2
2
4
4
0
0
-4
-4
2
2
4
4
0(无意义)
-4
0
-4
2
2
4
4
0(无意义)
-4
0
-4
>
=
<
<
=
>
>
<
>
<
<
>
-4>-6
-2×2>-6×2
-2÷2>-6÷2
-4>-6
-2×(-2) <-6×(-2)
-2÷(-2)<-6÷(-2)
×3
÷3
(或 )
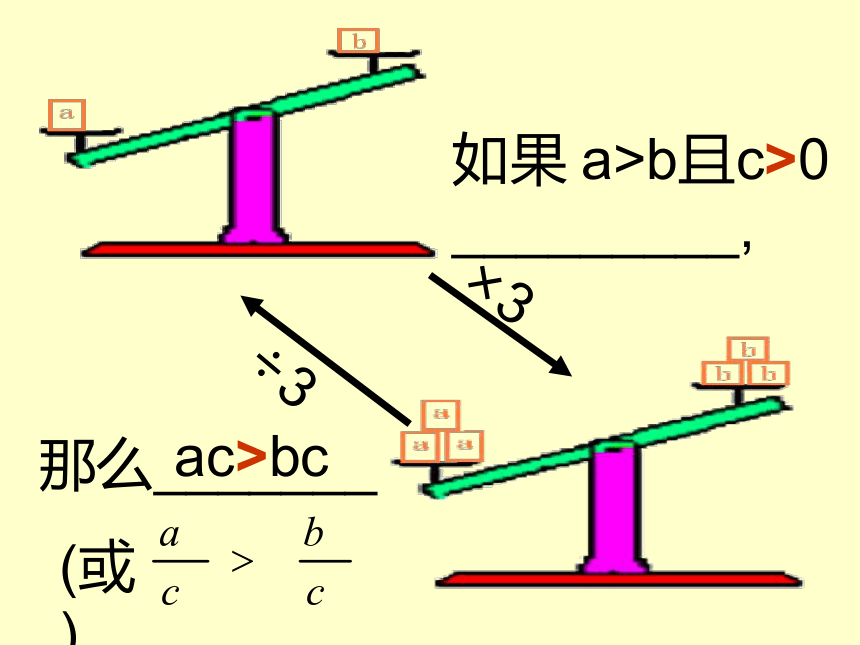
如果_________,
那么_______
a>b且c>0
ac>bc
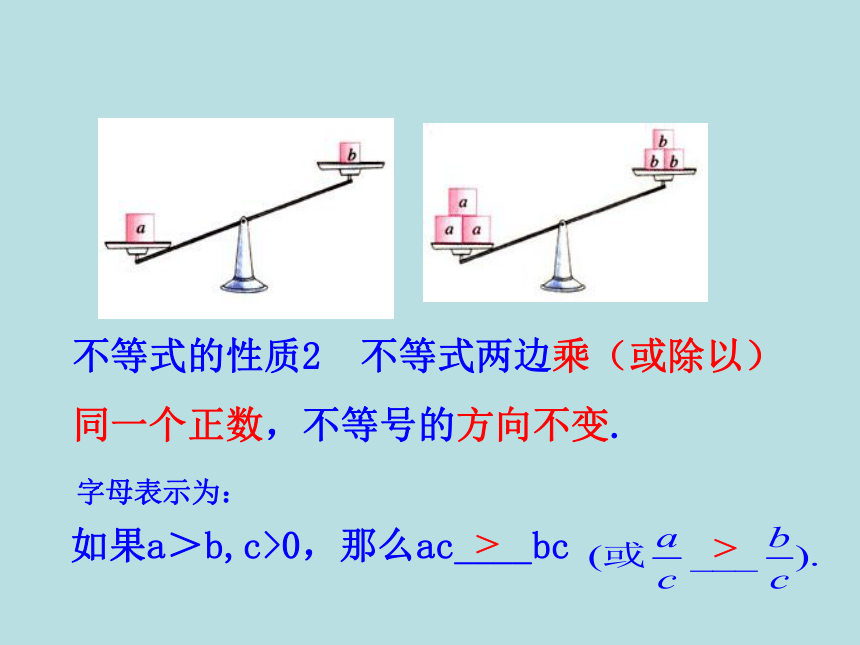
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,那么ac____bc
字母表示为:
>
>
字母表示为:
如果a>b,c<0,那么ac ____bc
﹤
﹤
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 3____b - 3;
(2) a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
例1:
?判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; ?(2)a-1 _____-1;
(3)3a______0; (4)- ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
【例】利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1;
(3) x﹥50; (4)-4x﹥3.
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
【解析】(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图所示:
0
33
为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得
3x-2x﹤2x+1-2x x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
为了使不等式 x﹥50中不等号的一边变为x,根据不等
式的性质2,不等式的两边都除以 不等号的方向不变,
得
x﹥75
这个不等式的解集在数轴上的表示如图所示:
0
75
为了使不等式-4x﹥3中的不等号的一边变为x,根据
______________,不等式两边都除以____,不等号的方
向______,得
x﹤-
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
利用不等式的性质解下列不等式.
(2)-2x 3
>
(1)x-5 -1
>
(3)7x 6x-6
<
【解析】
根据不等式的性质______,
两边都__________,得
x>-1+5
即
x>4
1
加上5
(1)x-5 -1
>
根据不等式的性质_____,两边都_______,得
3
除以-2
(2)-2x 3
>
根据不等式的性质____,两边都_______,得
7x-6x<-6
即
x<-6
1
减去6x
(3)7x 6x -6
<
1.判断正误:
(1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.
×
×
√
2.已知不等式2a+3b>3a+2b,试比较a、b的大小.
解:根据不等式的性质1,不等式两边都减去(2a+2b),得
2a+3b-(2a+2b)>3a+2b-(2a+2b)
2a+3b-2a-2b>3a+2b-2a-2b
所以b>a.
1.填空:
(1) 因为 2a<3a ,所以a是____数.
(3) 因为ax1, 所以a是____数.
(2) 因为 ,所以a是____数.
正
正
负
2.(无锡?中考)若a>b,则 ( )
(A)a>-b (B)a<-b
(C)-2a>-2b (D)-2a<-2b
【解析】选D.不等式的两边都乘以-2,不等号的方向改变.
3.(上海·中考)如果a>b,c<0,那么下列不等式成立的是( )
(A)a+c>b+c (B)c-a>c-b
(C)ac>bc (D)
【解析】选A.由不等式的性质1可知,a+c>b+c正确.
4.(泰州·中考)不等式2x+1>-5的解集是 .
【解析】2x>-6,x>-3.
答案:x>-3
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0 那么ac
如果a=b, 能否得到a+2=b+2 ?
如果a=b, 能否得到0.5a=0.5b ?
如果a=b, 能否得到-2a= -2b ?
如果a=b, 能否得到a-2=b-2 ?
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
(1)5>3, 5+2___3+2 , 5-2___3-2 ;
(2)-1<3, -1+2___3+2 , -1-3___3-3 ;
根据发现的规律填空:当不等式两边加或减同一个数(正数
或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
用“﹥”或“﹤”填空,并总结其中的规律:
数学小实验
器材:几个不等式,自己想出一些数;
操作:在“□”内按要求填上数字,在“ ”上填上“>”、“<”或“=”号;
观察:不等号的前后变化规律
要求:分工合作,认真操作,仔细观察,发现规律。
不等式
两边加上同一个数
两边减去同一个数
5>3
5+□ 3+□
5-□ 3-□
5+□ 3+□
5-□ 3-□
5+□ 3+□
5-□ 3-□
-1<3
-1+□ 3+□
-1-□ 3-□
-1+□ 3+□
-1-□ 3-□
-1+□ 3+□
-1-□ 3-□
自主设计
结论
探究一
4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
>
>
>
>
>
>
<
<
<
<
<
<
-2>-5
-2+3>-5+3
-2-4>-5-4
+ C
-C
(或________)
如果_____,
那么_______
如果a>b,
那么a±c>b±c
a>b
a+c>b+c
a-c>b-c
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
字母表示为:
如果a>b,那么a±c____b±c
﹥
(3) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4)–2<3, (-2)×6___3×6 , (-2) ×(-6)___3×(-6 )
当不等式两边乘同一个正数时,不等号的方向_____;
不变
而乘同一个负数时,不等号的方向_____;
改变
﹥
﹤
﹤
﹥
不等式还有什么类似的性质呢?
不等式
两边加上同一个数
两边减去同一个数
6>2
6×□ 2×□
6÷□ 2÷□
6×□ 2×□
6÷□ 2÷□
6×□ 2×□
6÷□ 2÷□
6×□ 2×□
6÷□ 2÷□
-2<3
-2×□ 3×□
-2÷□ 3÷□
-2×□ 3×□
-2÷□ 3÷□
-2×□ 3×□
-2÷□ 3÷□
-2×□ 3×□
-2÷□ 3÷□
自主设计
结论
探究二
数学小实验
器材:几个不等式,自己想出一些数;
操作:在“□”内按要求填上数字,在“ ”上填上“>”、“<”或“=”号;
观察:不等号的前后变化规律
要求:分工合作,认真操作,仔细观察,发现规律。
2
2
4
4
0
-4
>
<
0
-4
2
2
4
4
0
0
-4
-4
2
2
4
4
0(无意义)
-4
0
-4
2
2
4
4
0(无意义)
-4
0
-4
>
=
<
<
=
>
>
<
>
<
<
>
-4>-6
-2×2>-6×2
-2÷2>-6÷2
-4>-6
-2×(-2) <-6×(-2)
-2÷(-2)<-6÷(-2)
×3
÷3
(或 )
如果_________,
那么_______
a>b且c>0
ac>bc
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,那么ac____bc
字母表示为:
>
>
字母表示为:
如果a>b,c<0,那么ac ____bc
﹤
﹤
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 3____b - 3;
(2) a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
例1:
?判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; ?(2)a-1 _____-1;
(3)3a______0; (4)- ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
【例】利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1;
(3) x﹥50; (4)-4x﹥3.
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
【解析】(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图所示:
0
33
为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得
3x-2x﹤2x+1-2x x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
为了使不等式 x﹥50中不等号的一边变为x,根据不等
式的性质2,不等式的两边都除以 不等号的方向不变,
得
x﹥75
这个不等式的解集在数轴上的表示如图所示:
0
75
为了使不等式-4x﹥3中的不等号的一边变为x,根据
______________,不等式两边都除以____,不等号的方
向______,得
x﹤-
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
利用不等式的性质解下列不等式.
(2)-2x 3
>
(1)x-5 -1
>
(3)7x 6x-6
<
【解析】
根据不等式的性质______,
两边都__________,得
x>-1+5
即
x>4
1
加上5
(1)x-5 -1
>
根据不等式的性质_____,两边都_______,得
3
除以-2
(2)-2x 3
>
根据不等式的性质____,两边都_______,得
7x-6x<-6
即
x<-6
1
减去6x
(3)7x 6x -6
<
1.判断正误:
(1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.
×
×
√
2.已知不等式2a+3b>3a+2b,试比较a、b的大小.
解:根据不等式的性质1,不等式两边都减去(2a+2b),得
2a+3b-(2a+2b)>3a+2b-(2a+2b)
2a+3b-2a-2b>3a+2b-2a-2b
所以b>a.
1.填空:
(1) 因为 2a<3a ,所以a是____数.
(3) 因为ax1, 所以a是____数.
(2) 因为 ,所以a是____数.
正
正
负
2.(无锡?中考)若a>b,则 ( )
(A)a>-b (B)a<-b
(C)-2a>-2b (D)-2a<-2b
【解析】选D.不等式的两边都乘以-2,不等号的方向改变.
3.(上海·中考)如果a>b,c<0,那么下列不等式成立的是( )
(A)a+c>b+c (B)c-a>c-b
(C)ac>bc (D)
【解析】选A.由不等式的性质1可知,a+c>b+c正确.
4.(泰州·中考)不等式2x+1>-5的解集是 .
【解析】2x>-6,x>-3.
答案:x>-3
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0 那么ac
