人教版七年级数学下册第9章第2节一元一次不等式 (2)(共29张PPT)
文档属性
| 名称 | 人教版七年级数学下册第9章第2节一元一次不等式 (2)(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览








文档简介
9.2 一元一次不等式
学习目标:
(1)了解一元一次不等式的概念,掌握一元一次不等式的解法.
(2) 在依据不等式的性质探究一元一次不等式解法过程中,加深对类比和化归思想的体会.
学习重点:
一元一次不等式的解法.
1、不等式有什么性质?
性质3:不等式两边乘(或除以)同一个负数,不等号的方向 。
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向 。
性质2:不等式两边乘(或除以)同一个正数,不等号的方向
。
如果
,那么
;
如果
,
,那么
(或
);
如果
,
,那么
(或
)。
不变
不变
改变
复习回顾
2、一元一次方程的定义:
【一元一次方程 】“只含一个未知数、并且未知数的项的次数是1”的方程.
复习回顾
1、思考:观察下列不等式,它们有哪些共同特点?
,
,
,
可以发现,上述每个不等式都只有含有一个未知数,并且未知数的项的次数都是1,类似于一元一次方程,含有一个未知数,未知数的次数都是1的不等式叫做一元一次不等式。
注意:与一元一次方程也类似,一元一次不等式的两边也要
求是整式。
探究一
归纳一元一次不等式定义:
2x
5
<3+x
只含有一个未知数,未知数的项的最高次数是1的不等式叫做一元一次不等式.
不是一元一次不等式
不等号的两边都是整式,
探究一
1、下列不等式中哪些是一元一次不等式?
?
?
?
?
?
尝试应用
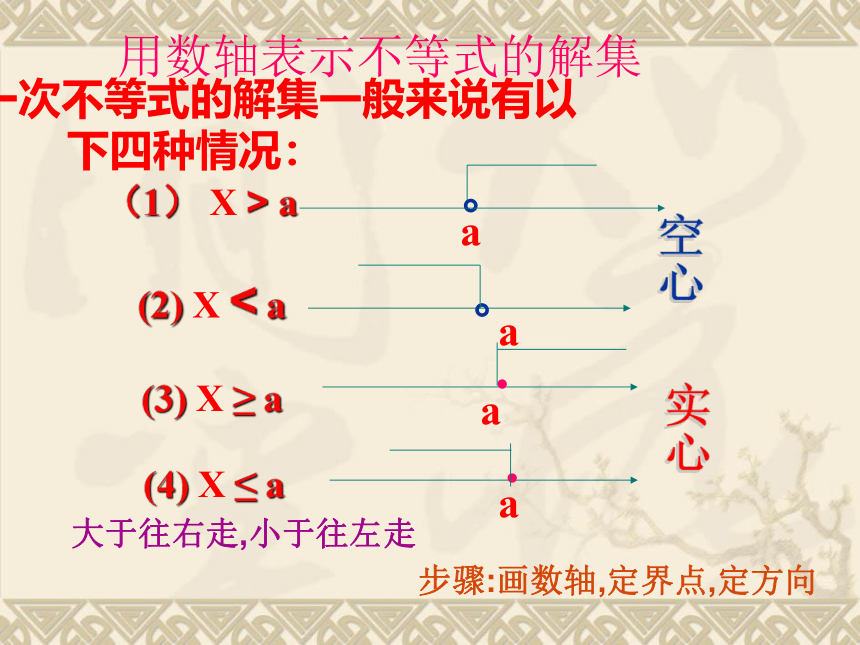
用数轴表示不等式的解集
一元一次不等式的解集一般来说有以下四种情况:
(1) X > a
(2) X < a
(3) X ≥ a
(4) X ≤ a
a
a
.
a
a
.
步骤:画数轴,定界点,定方向
大于往右走,小于往左走
练习 利用不等式的性质解不等式:
解:根据不等式的性质1,不等式的两边加7,
不等号的方向不变,所以
探究二
x>26+7
x-7>26
x-7+7>26+7
x>33
移项
x<10 - 3
+ 3
-3
x + 3 - 3 < 10 - 3
方程中的移项法则在不等式中仍然适用!
移项要变号,不影响不等号的方向
x + 3 < 10
x<10-3
2. 比一比.
解:
(1)3(x-2)+2=x
(2)3(x-2)+2<x
3x-6+2=x
3x-6+2<x
3x-x=+ 6-2
3x-x<+ 6-2
2x=4
2x<4
x=2
x<2
(1)3(x-2)+2=x
(2)3(x-2)+2<x
解一元一次方程与解一元一次不等式的方法、步骤类似.
①
⑤
④
③
②
步骤
>
6-2 (x-2) =3x
6-2x+4=3x
-2x -3x=-6-4
-5x=-10
x=2
x<2
6-2 (x-2) >3x
6-2x+4 >3x
-2x -3x >-6-4
-5x >-10
不等式的方法、步骤都类似的结论,同桌一起完成以下两题,并将
解题过程填入表(一)。
表(一)
(1)利用解一元一次方程与解一元一次
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
与解一元一次方程方法类似
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
﹦
﹦
﹦
﹦
﹦
﹦
0
1
2
-1
3
4
5
6
7
8
这个不等式的解集在数轴上的表示为
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
求满足不等式 8x-2≤7x+3 的正整数解
解不等式3+3x>2+4x
解:移项,得 3-2> 4x-3x
合并同类项,得 1>x
∴ 原不等式的解集是 x<1
写不等式的解集时,要把表示未知数的字母写在不等号的左边。
例如
例3 解不等式
3(1-x)>2(1-2x)
解: 去括号,得 3-3 x >2-4x
移项,得 -3 x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是 x >-1
解:去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
这个不等式的解集在数轴上的表示如图所示.
特别注意,当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变.
展示交流
(不等式性质2)
(不等式性质3)
比一比,谁做得又快又好!
(1)x+4>3
(2)7x+6 ≥ 6x+3
(3)7x-1 ≤ 6x+1
(4)3-5x < 2(2-3x)
解下列不等式,并把它们的解集在数轴上
表示出来。
例
解一元一次方程的依据是等式的性质.
解一元一次方程的一般步骤是:
去分母,去括号,移项,合并同类项,系数化为1.
问题2 回忆解一元一次方程的依据和一般步骤,对你解一元一次不等式有什么启发?
(一般地,利用不等式的性质,采取与解一元一次方程相类似的步骤,就可以求出一元一次不等式的解集。)
步骤
依据
去分母
去括号
移项
合并同类项
系数化为1
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
归纳:1、 解一元一次不等式的步骤,及每一步变形的依据是什么?
展示交流
注意事项:
6.将求得的解集在数轴上表示
展示交流
归纳:2、解一元一次不等式和解一元一次方程
有哪些相同和不同之处?
相同之处:
(1)基本步骤相同;(2)基本思想相同:将一元一次方程或一元一次不等式变形为最简形式.
不同之处:
(1)一元一次不等式两边都(或除以)同一个负数时,不等号的方向改变;而方程两边乘(或除以)同一个负数时,等号不变.
(2)一元一次不等式有无限多个解,而一元一次方程只有一个解.
展示交流
1、下列不等式的解法正确吗?如果不正确,请改正:
(1)-2x<-4.
解:系数化为1,得x<-2;
不正确.应改为x>2.
(2) x+1<2x-3.
解:移项,得 x+2x<-3+1.
合并同类项,得___________
不正确.
系数化为1,得__________
尝试应用
—
—
-x<-4
x>4
1、下列不等式的解法正确吗?如果不正确,请改正:
(3)2-3(x-4)<2(x-2).
解:去括号,得2-3x-4<2x-2;
不正确.应改为2-3x+12<2x-4.
(4)
去括号,得 2x+2≥6x-5+1
试试看,你能找出几处错误?
解:去分母,得 2(x+1)≥3(2x-5)+1
合并同类项,得 -4x≥-6
移项,得 2x-6x≥-5+1 -2
尝试应用
12
15 + 12
-15 + 12
系数化为1,得 x≥
-5
≤
5
4
通过本课时的学习,需要我们掌握:
1.一元一次不等式的概念;
2.一元一次不等式的解法与一元一次方程的解法类似,
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)化系数为1(有时不等号的方向会改变哦!)
小结
练习1: m取何值时,关于x的方程
的解大于1。
解答:解这个方程:
∴
根据题意,得
解得 m>2
练习2:解关于x的不等式: k(x+3)>x+4;
解:去括号,得kx+3k>x+4;
移项得kx-x > 4 -3k ; 得(k-1)x > 4 -3k ;
若k-1=0, 即k=1时,0>1不成立,
∴不等式无解。
若k-1>0,即k>1时,
若k-1<0,即k<1时,
。
练习3.根据下列条件,分别求出a的值或取值范围:
1)已知不等式 的解集是x<5;
2)已知x=5是不等式 的解.
解:
1).2x-4>3x+a
2x-3x>a+4
-x>(a+4)
∴解集是:x<-a-4
∵解集是x<5
∴-a-4=5
得a=-9
2).据题意有:
即6>15+a
∴ -9>a
解得:a<-9
注意:变号!
一次环保知识竞赛共有20道题,规定答对一道题得5分,不答得0分,答错一道题扣2分.在这次竞赛中,小明有一题没答,小明的分数超过80分,小明至多答错了几道题?
练习4:
解 设小明答错了X道题,
由题意得: 5(20-1-X)-2X > 80
解得
答: 小明至多答错了2道题.
学习目标:
(1)了解一元一次不等式的概念,掌握一元一次不等式的解法.
(2) 在依据不等式的性质探究一元一次不等式解法过程中,加深对类比和化归思想的体会.
学习重点:
一元一次不等式的解法.
1、不等式有什么性质?
性质3:不等式两边乘(或除以)同一个负数,不等号的方向 。
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向 。
性质2:不等式两边乘(或除以)同一个正数,不等号的方向
。
如果
,那么
;
如果
,
,那么
(或
);
如果
,
,那么
(或
)。
不变
不变
改变
复习回顾
2、一元一次方程的定义:
【一元一次方程 】“只含一个未知数、并且未知数的项的次数是1”的方程.
复习回顾
1、思考:观察下列不等式,它们有哪些共同特点?
,
,
,
可以发现,上述每个不等式都只有含有一个未知数,并且未知数的项的次数都是1,类似于一元一次方程,含有一个未知数,未知数的次数都是1的不等式叫做一元一次不等式。
注意:与一元一次方程也类似,一元一次不等式的两边也要
求是整式。
探究一
归纳一元一次不等式定义:
2x
5
<3+x
只含有一个未知数,未知数的项的最高次数是1的不等式叫做一元一次不等式.
不是一元一次不等式
不等号的两边都是整式,
探究一
1、下列不等式中哪些是一元一次不等式?
?
?
?
?
?
尝试应用
用数轴表示不等式的解集
一元一次不等式的解集一般来说有以下四种情况:
(1) X > a
(2) X < a
(3) X ≥ a
(4) X ≤ a
a
a
.
a
a
.
步骤:画数轴,定界点,定方向
大于往右走,小于往左走
练习 利用不等式的性质解不等式:
解:根据不等式的性质1,不等式的两边加7,
不等号的方向不变,所以
探究二
x>26+7
x-7>26
x-7+7>26+7
x>33
移项
x<10 - 3
+ 3
-3
x + 3 - 3 < 10 - 3
方程中的移项法则在不等式中仍然适用!
移项要变号,不影响不等号的方向
x + 3 < 10
x<10-3
2. 比一比.
解:
(1)3(x-2)+2=x
(2)3(x-2)+2<x
3x-6+2=x
3x-6+2<x
3x-x=+ 6-2
3x-x<+ 6-2
2x=4
2x<4
x=2
x<2
(1)3(x-2)+2=x
(2)3(x-2)+2<x
解一元一次方程与解一元一次不等式的方法、步骤类似.
①
⑤
④
③
②
步骤
>
6-2 (x-2) =3x
6-2x+4=3x
-2x -3x=-6-4
-5x=-10
x=2
x<2
6-2 (x-2) >3x
6-2x+4 >3x
-2x -3x >-6-4
-5x >-10
不等式的方法、步骤都类似的结论,同桌一起完成以下两题,并将
解题过程填入表(一)。
表(一)
(1)利用解一元一次方程与解一元一次
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
与解一元一次方程方法类似
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
﹦
﹦
﹦
﹦
﹦
﹦
0
1
2
-1
3
4
5
6
7
8
这个不等式的解集在数轴上的表示为
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
求满足不等式 8x-2≤7x+3 的正整数解
解不等式3+3x>2+4x
解:移项,得 3-2> 4x-3x
合并同类项,得 1>x
∴ 原不等式的解集是 x<1
写不等式的解集时,要把表示未知数的字母写在不等号的左边。
例如
例3 解不等式
3(1-x)>2(1-2x)
解: 去括号,得 3-3 x >2-4x
移项,得 -3 x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是 x >-1
解:去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
这个不等式的解集在数轴上的表示如图所示.
特别注意,当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变.
展示交流
(不等式性质2)
(不等式性质3)
比一比,谁做得又快又好!
(1)x+4>3
(2)7x+6 ≥ 6x+3
(3)7x-1 ≤ 6x+1
(4)3-5x < 2(2-3x)
解下列不等式,并把它们的解集在数轴上
表示出来。
例
解一元一次方程的依据是等式的性质.
解一元一次方程的一般步骤是:
去分母,去括号,移项,合并同类项,系数化为1.
问题2 回忆解一元一次方程的依据和一般步骤,对你解一元一次不等式有什么启发?
(一般地,利用不等式的性质,采取与解一元一次方程相类似的步骤,就可以求出一元一次不等式的解集。)
步骤
依据
去分母
去括号
移项
合并同类项
系数化为1
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
归纳:1、 解一元一次不等式的步骤,及每一步变形的依据是什么?
展示交流
注意事项:
6.将求得的解集在数轴上表示
展示交流
归纳:2、解一元一次不等式和解一元一次方程
有哪些相同和不同之处?
相同之处:
(1)基本步骤相同;(2)基本思想相同:将一元一次方程或一元一次不等式变形为最简形式.
不同之处:
(1)一元一次不等式两边都(或除以)同一个负数时,不等号的方向改变;而方程两边乘(或除以)同一个负数时,等号不变.
(2)一元一次不等式有无限多个解,而一元一次方程只有一个解.
展示交流
1、下列不等式的解法正确吗?如果不正确,请改正:
(1)-2x<-4.
解:系数化为1,得x<-2;
不正确.应改为x>2.
(2) x+1<2x-3.
解:移项,得 x+2x<-3+1.
合并同类项,得___________
不正确.
系数化为1,得__________
尝试应用
—
—
-x<-4
x>4
1、下列不等式的解法正确吗?如果不正确,请改正:
(3)2-3(x-4)<2(x-2).
解:去括号,得2-3x-4<2x-2;
不正确.应改为2-3x+12<2x-4.
(4)
去括号,得 2x+2≥6x-5+1
试试看,你能找出几处错误?
解:去分母,得 2(x+1)≥3(2x-5)+1
合并同类项,得 -4x≥-6
移项,得 2x-6x≥-5+1 -2
尝试应用
12
15 + 12
-15 + 12
系数化为1,得 x≥
-5
≤
5
4
通过本课时的学习,需要我们掌握:
1.一元一次不等式的概念;
2.一元一次不等式的解法与一元一次方程的解法类似,
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)化系数为1(有时不等号的方向会改变哦!)
小结
练习1: m取何值时,关于x的方程
的解大于1。
解答:解这个方程:
∴
根据题意,得
解得 m>2
练习2:解关于x的不等式: k(x+3)>x+4;
解:去括号,得kx+3k>x+4;
移项得kx-x > 4 -3k ; 得(k-1)x > 4 -3k ;
若k-1=0, 即k=1时,0>1不成立,
∴不等式无解。
若k-1>0,即k>1时,
若k-1<0,即k<1时,
。
练习3.根据下列条件,分别求出a的值或取值范围:
1)已知不等式 的解集是x<5;
2)已知x=5是不等式 的解.
解:
1).2x-4>3x+a
2x-3x>a+4
-x>(a+4)
∴解集是:x<-a-4
∵解集是x<5
∴-a-4=5
得a=-9
2).据题意有:
即6>15+a
∴ -9>a
解得:a<-9
注意:变号!
一次环保知识竞赛共有20道题,规定答对一道题得5分,不答得0分,答错一道题扣2分.在这次竞赛中,小明有一题没答,小明的分数超过80分,小明至多答错了几道题?
练习4:
解 设小明答错了X道题,
由题意得: 5(20-1-X)-2X > 80
解得
答: 小明至多答错了2道题.
