人教版数学七年级下册 7.1.2 平面直角坐标系(二)课件(共21张PPT)
文档属性
| 名称 | 人教版数学七年级下册 7.1.2 平面直角坐标系(二)课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 21:07:52 | ||
图片预览






文档简介
2.两条坐标轴如何称呼,方向如何确定?
知识回顾
1.什么是平面直角坐标系?
4.平面内点的坐标由几部分组成?
3.什么是点的坐标?
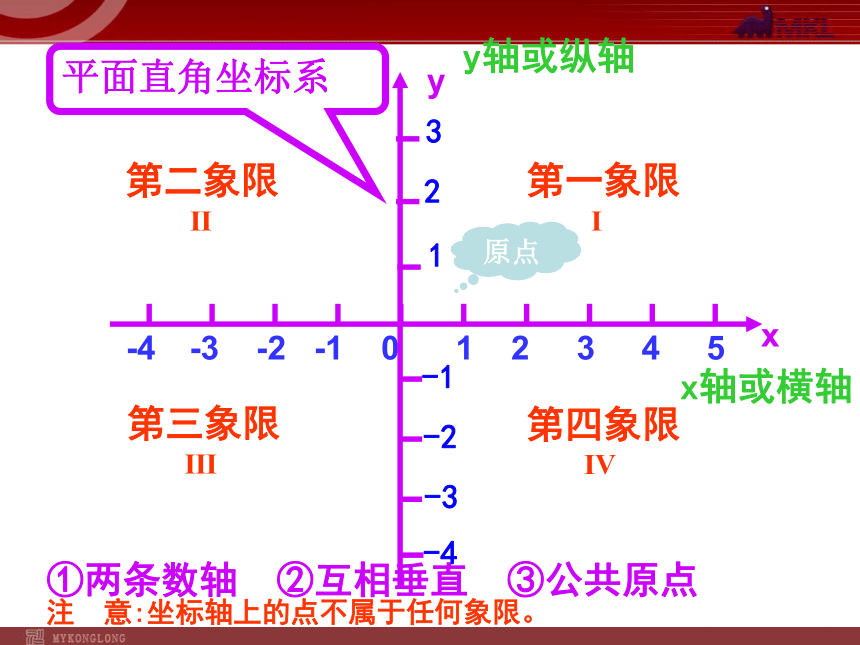
平面直角坐标系
原点
y轴或纵轴
x轴或横轴
①两条数轴 ②互相垂直 ③公共原点
x
-4 -3 -2 -1 0 1 2 3 4 5
y
3
2
1
-1
-2
-3
-4
第二象限
Ⅱ
第一象限
Ⅰ
第三象限
Ⅲ
第四象限
Ⅳ
注 意:坐标轴上的点不属于任何象限。
( 4,5 )
( -4,- 1 )
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
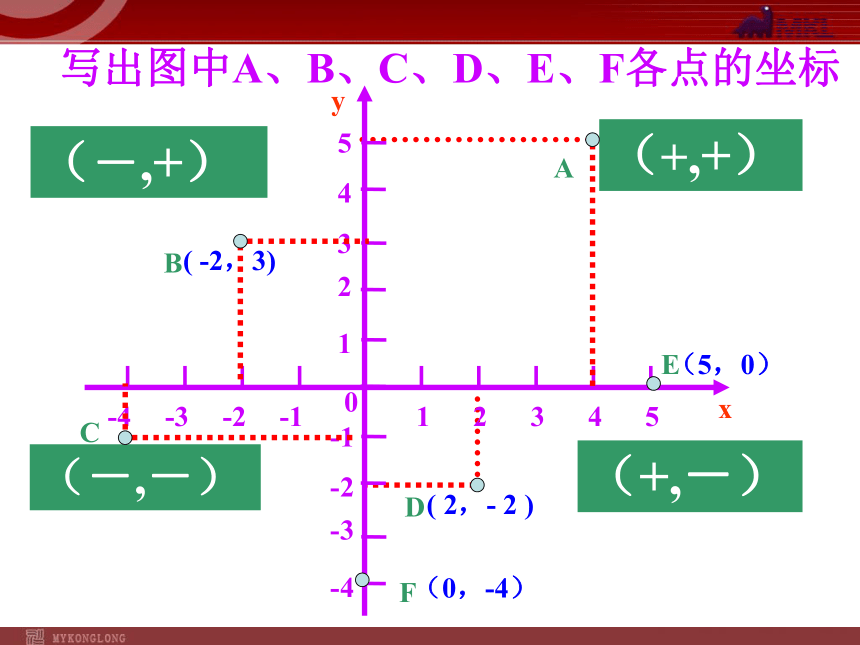
( -2,3)
(5,0)
(0,-4)
(-,+)
(-,-)
(+,-)
写出图中A、B、C、D、E、F各点的坐标
(+,+)
( 2,- 2 )
A
B
C
D
E
F
1、第一、二、三、四象限内的坐标的符号分别是(+,+),(-,+),(-,-),(+, -)
2、坐标轴上的点坐标至少有一个是0
横轴上的点的纵坐标为0,表示为(x,0)
纵轴上的点的横坐标为0.表示为(0,y)
原点的坐标为(0,0)
结论1
练一练:
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
0
1
1
x
y
A
B
C
D
E
F
G
H
如图,分别写出八边形各个顶点的坐标。
(7,2)
(4,5)
(-1,5)
(-4,2)
(-4,-3)
(-1,-6)
(4,-6)
(7,-3)
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
结论2
1、第一、二、三、四象限内的坐标的符号
分别是(+,+),(-,+),(-,-),(+, -)
2、坐标轴的点至少有一个是0
x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
3、纵坐标相同的点的连线平行于x轴
4、横坐标相同的点的连线平行于y轴
o
2
4
6
8
2
4
6
8
y
x
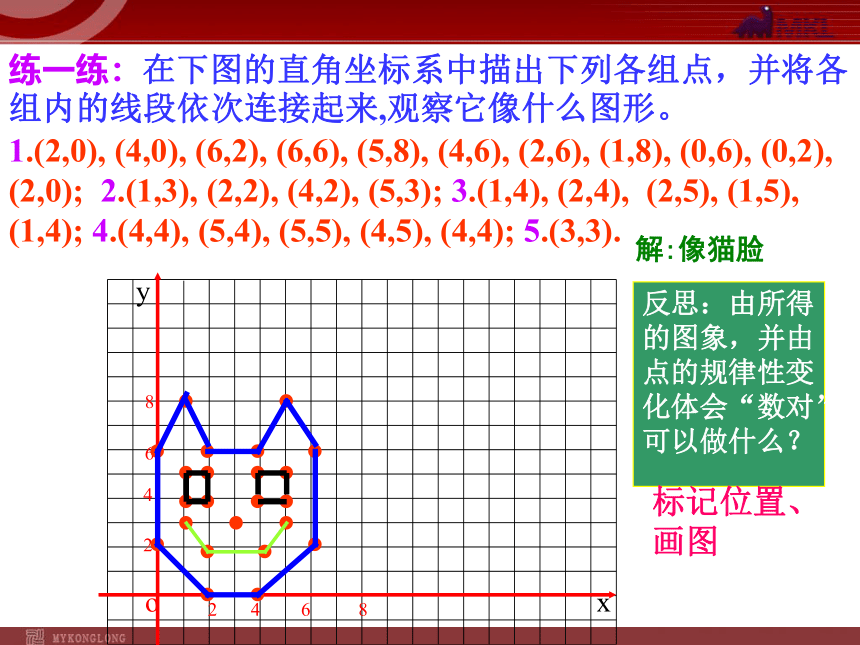
练一练:在下图的直角坐标系中描出下列各组点,并将各组内的线段依次连接起来,观察它像什么图形。
1.(2,0), (4,0), (6,2), (6,6), (5,8), (4,6), (2,6), (1,8), (0,6), (0,2), (2,0); 2.(1,3), (2,2), (4,2), (5,3); 3.(1,4), (2,4), (2,5), (1,5), (1,4); 4.(4,4), (5,4), (5,5), (4,5), (4,4); 5.(3,3).
反思:由所得
的图象,并由
点的规律性变
化体会“数对”
可以做什么?
解:像猫脸
标记位置、
画图
五位同学做游戏,位置如图,建立适当的直角坐标系,写出这五个同学所在位置的坐标.
1
2
3
-3
x
-2
o
-4
-1
y
4
2
5
3
6
-2
-3
-1
1
例1, 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的
坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,以点C为坐标原点,分别以CD,CB所在的直线为x 轴,y 轴建立直角坐标系.此时C点坐标为(0,0)由CD长为6,CB长为4, 可得D,B,A的坐标分别为D( 6,0 ),B(0,4),A(6,4)
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
1
1
1.在上面的例题中,你还可以怎样
建立直角坐标系?
2.你认为怎样建立适合的直角
坐标系?
议
一
议
例1, 如图, 矩形ABCD的长宽分别是6 , 4 ,
建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,分别以两对边中
点的连线为x轴,y轴建立
直角坐标系.此时各顶点
坐标为A(3,2),B(-3,2),
C(-3,-2),D(3,-2 ) .
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数
点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数
点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数
1
2
3
4
5
-4
-3
-2
-1
·
O
X
P(3,2)
·
B(3,-2)
A(-3,2)
C(-3,- 2 )
·
·
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
3
1
4
2
5
-2
-4
-1
-3
★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )
a,-b
- a, b
-a,-b
练一练
巩固练习:
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
4.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是________。
3.点 M(- 8,12)到 x轴的距离是_________,
到 y轴的距离是________.
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
5.点A(1-a,5),B(3 ,b)关于y轴对称,
则a=___,b=____。
四
三
y
-1
(4,0)或(-4,0)
12
8
(-1.5,-2)
4
5
7.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
8.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】.
(A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限
B
a<0
b>1
B
在一次“寻宝”游戏中,寻宝人已经找到了坐标为
(3,2)和(3,-2)的两个标志点,并且知道藏宝
地点的坐标为(4,4),除此之外不知道其他信息,
如何确定直角坐标系找到“宝藏”?请跟同伴交流。
·
1
2
3
4
5
-4
-3
-2
-1
·
O
(3,-2)
X
(3,2)
·
考考你
3
1
4
2
5
-2
-4
-1
-3
(4,4)
·
告诉大家
本节课你的收获!
象限中点的坐标符号的情况及坐标轴上点的坐标特点
如何根据实际,建立平面直角坐标系,
使问题简单、快捷
平行坐标轴的点坐标的特点,关于X轴,
Y轴及原点对称的坐标的特点
Goodbye everyone!
知识回顾
1.什么是平面直角坐标系?
4.平面内点的坐标由几部分组成?
3.什么是点的坐标?
平面直角坐标系
原点
y轴或纵轴
x轴或横轴
①两条数轴 ②互相垂直 ③公共原点
x
-4 -3 -2 -1 0 1 2 3 4 5
y
3
2
1
-1
-2
-3
-4
第二象限
Ⅱ
第一象限
Ⅰ
第三象限
Ⅲ
第四象限
Ⅳ
注 意:坐标轴上的点不属于任何象限。
( 4,5 )
( -4,- 1 )
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
( -2,3)
(5,0)
(0,-4)
(-,+)
(-,-)
(+,-)
写出图中A、B、C、D、E、F各点的坐标
(+,+)
( 2,- 2 )
A
B
C
D
E
F
1、第一、二、三、四象限内的坐标的符号分别是(+,+),(-,+),(-,-),(+, -)
2、坐标轴上的点坐标至少有一个是0
横轴上的点的纵坐标为0,表示为(x,0)
纵轴上的点的横坐标为0.表示为(0,y)
原点的坐标为(0,0)
结论1
练一练:
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
0
1
1
x
y
A
B
C
D
E
F
G
H
如图,分别写出八边形各个顶点的坐标。
(7,2)
(4,5)
(-1,5)
(-4,2)
(-4,-3)
(-1,-6)
(4,-6)
(7,-3)
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
结论2
1、第一、二、三、四象限内的坐标的符号
分别是(+,+),(-,+),(-,-),(+, -)
2、坐标轴的点至少有一个是0
x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
3、纵坐标相同的点的连线平行于x轴
4、横坐标相同的点的连线平行于y轴
o
2
4
6
8
2
4
6
8
y
x
练一练:在下图的直角坐标系中描出下列各组点,并将各组内的线段依次连接起来,观察它像什么图形。
1.(2,0), (4,0), (6,2), (6,6), (5,8), (4,6), (2,6), (1,8), (0,6), (0,2), (2,0); 2.(1,3), (2,2), (4,2), (5,3); 3.(1,4), (2,4), (2,5), (1,5), (1,4); 4.(4,4), (5,4), (5,5), (4,5), (4,4); 5.(3,3).
反思:由所得
的图象,并由
点的规律性变
化体会“数对”
可以做什么?
解:像猫脸
标记位置、
画图
五位同学做游戏,位置如图,建立适当的直角坐标系,写出这五个同学所在位置的坐标.
1
2
3
-3
x
-2
o
-4
-1
y
4
2
5
3
6
-2
-3
-1
1
例1, 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的
坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,以点C为坐标原点,分别以CD,CB所在的直线为x 轴,y 轴建立直角坐标系.此时C点坐标为(0,0)由CD长为6,CB长为4, 可得D,B,A的坐标分别为D( 6,0 ),B(0,4),A(6,4)
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
1
1
1.在上面的例题中,你还可以怎样
建立直角坐标系?
2.你认为怎样建立适合的直角
坐标系?
议
一
议
例1, 如图, 矩形ABCD的长宽分别是6 , 4 ,
建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,分别以两对边中
点的连线为x轴,y轴建立
直角坐标系.此时各顶点
坐标为A(3,2),B(-3,2),
C(-3,-2),D(3,-2 ) .
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数
点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数
点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数
1
2
3
4
5
-4
-3
-2
-1
·
O
X
P(3,2)
·
B(3,-2)
A(-3,2)
C(-3,- 2 )
·
·
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
3
1
4
2
5
-2
-4
-1
-3
★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )
a,-b
- a, b
-a,-b
练一练
巩固练习:
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
4.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是________。
3.点 M(- 8,12)到 x轴的距离是_________,
到 y轴的距离是________.
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
5.点A(1-a,5),B(3 ,b)关于y轴对称,
则a=___,b=____。
四
三
y
-1
(4,0)或(-4,0)
12
8
(-1.5,-2)
4
5
7.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
8.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】.
(A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限
B
a<0
b>1
B
在一次“寻宝”游戏中,寻宝人已经找到了坐标为
(3,2)和(3,-2)的两个标志点,并且知道藏宝
地点的坐标为(4,4),除此之外不知道其他信息,
如何确定直角坐标系找到“宝藏”?请跟同伴交流。
·
1
2
3
4
5
-4
-3
-2
-1
·
O
(3,-2)
X
(3,2)
·
考考你
3
1
4
2
5
-2
-4
-1
-3
(4,4)
·
告诉大家
本节课你的收获!
象限中点的坐标符号的情况及坐标轴上点的坐标特点
如何根据实际,建立平面直角坐标系,
使问题简单、快捷
平行坐标轴的点坐标的特点,关于X轴,
Y轴及原点对称的坐标的特点
Goodbye everyone!
