人教版七年级数学 下册8.2.2.2《用适当的方法解二元一次方程组》课件(共16张PPT)
文档属性
| 名称 | 人教版七年级数学 下册8.2.2.2《用适当的方法解二元一次方程组》课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览






文档简介
新人教版: 二元一次方程组的解法
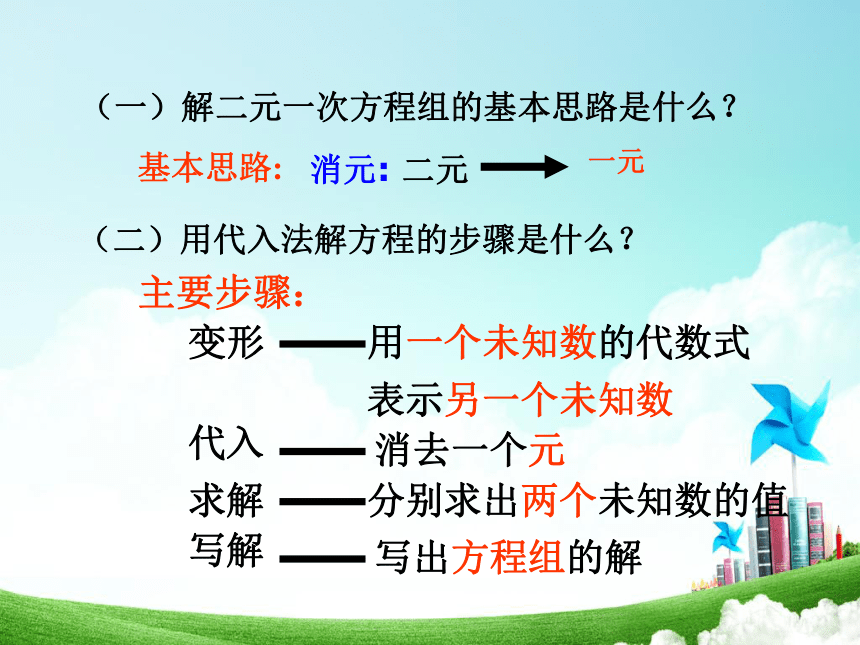
主要步骤:
基本思路:
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
(一)解二元一次方程组的基本思路是什么?
(二)用代入法解方程的步骤是什么?
一元
加减消元法的主要步骤:
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元
消去一个未知数后化为一元一次方程
求出一个未知数的值
写出方程组的解
同一个未知数的系数相同或互为相反数
回代
代入原方程求出另一个未知数的值
试一试:1:用代入法解方程组
y=x-3 ⑴
3x-8y=14 ⑵
小试牛刀:
分析:方程⑴中的(x-3)替换方程(2)中的y,从 而 达到消元的目的.
3x-8(x-3)=14
解:将(1)式代入(2)式中,得:
3X-8X+24=14
-5X=-10
X=2
所以, x=-2 是方程组的解。
y=-5
将X=-2回代到(1)式中得 :y =-5
试一试:2:用加减法解方程组
{
2x+y=40
x +y =22
思考:
1、用代入消元法怎么解此方程组?
2、观察y的系数,能否找出新的消元方法呢?
②
①
试一试:2:用加减法解方程组
x+3y =6 ⑴
x-2y=1 ⑵
分析:⑴-(2)可将未知数x消元。
3y-(-2)y=5
解:(1)-(2),得:
3y+2y=5
5y=5
y=1
所以, x=3 是方程组的解。
y=1
将y=1回代到(1)式中得 :x =3
①
②
解:由①+②得: 5x=10
把x=2代入①,得: y=3
x=2
所以原方程组的解是
2x -5y=7 ①
2x+3y=-1 ②
解方程组
解:由 ② -①得: 8y=-8
y=-1
把y=-1代入①,得: x=1
所以原方程组的解是
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
①
②
由①+②得: 5x=10
2x-5y=7 ①
2x+3y=-1 ②
由 ②-①得:8y=-8
{
3 x+4 y=16
5 x- 6 y=33
①
②
像这样的方程组能用加减消元法来解吗?
消元先看相同未知数系数的最小公倍数
解:?×5得:15x+20y=80......?
?×3得:15x-18y=99……
y=
将y=代入?得:x=6
-?得:(-18y)-(20y)=19
所以原方程组的解是
(1)
2x+y=3 ①
3x-5y=11 ②
(2)
2x+5y=1 ①
3x+2y=7 ②
2017年5月19日 录制
主要步骤:
基本思路:
写解
求解
代入
消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
(一)解二元一次方程组的基本思路是什么?
(二)用代入法解方程的步骤是什么?
一元
加减消元法的主要步骤:
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元
消去一个未知数后化为一元一次方程
求出一个未知数的值
写出方程组的解
同一个未知数的系数相同或互为相反数
回代
代入原方程求出另一个未知数的值
试一试:1:用代入法解方程组
y=x-3 ⑴
3x-8y=14 ⑵
小试牛刀:
分析:方程⑴中的(x-3)替换方程(2)中的y,从 而 达到消元的目的.
3x-8(x-3)=14
解:将(1)式代入(2)式中,得:
3X-8X+24=14
-5X=-10
X=2
所以, x=-2 是方程组的解。
y=-5
将X=-2回代到(1)式中得 :y =-5
试一试:2:用加减法解方程组
{
2x+y=40
x +y =22
思考:
1、用代入消元法怎么解此方程组?
2、观察y的系数,能否找出新的消元方法呢?
②
①
试一试:2:用加减法解方程组
x+3y =6 ⑴
x-2y=1 ⑵
分析:⑴-(2)可将未知数x消元。
3y-(-2)y=5
解:(1)-(2),得:
3y+2y=5
5y=5
y=1
所以, x=3 是方程组的解。
y=1
将y=1回代到(1)式中得 :x =3
①
②
解:由①+②得: 5x=10
把x=2代入①,得: y=3
x=2
所以原方程组的解是
2x -5y=7 ①
2x+3y=-1 ②
解方程组
解:由 ② -①得: 8y=-8
y=-1
把y=-1代入①,得: x=1
所以原方程组的解是
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
①
②
由①+②得: 5x=10
2x-5y=7 ①
2x+3y=-1 ②
由 ②-①得:8y=-8
{
3 x+4 y=16
5 x- 6 y=33
①
②
像这样的方程组能用加减消元法来解吗?
消元先看相同未知数系数的最小公倍数
解:?×5得:15x+20y=80......?
?×3得:15x-18y=99……
y=
将y=代入?得:x=6
-?得:(-18y)-(20y)=19
所以原方程组的解是
(1)
2x+y=3 ①
3x-5y=11 ②
(2)
2x+5y=1 ①
3x+2y=7 ②
2017年5月19日 录制
