苏科版 初中数学八年级上册2-5《等腰三角形的轴对称性》课件(24张)
文档属性
| 名称 | 苏科版 初中数学八年级上册2-5《等腰三角形的轴对称性》课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 292.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 11:04:14 | ||
图片预览


文档简介
等腰三角形的轴对称性
有两条边相等的三角形叫做等腰三角形.
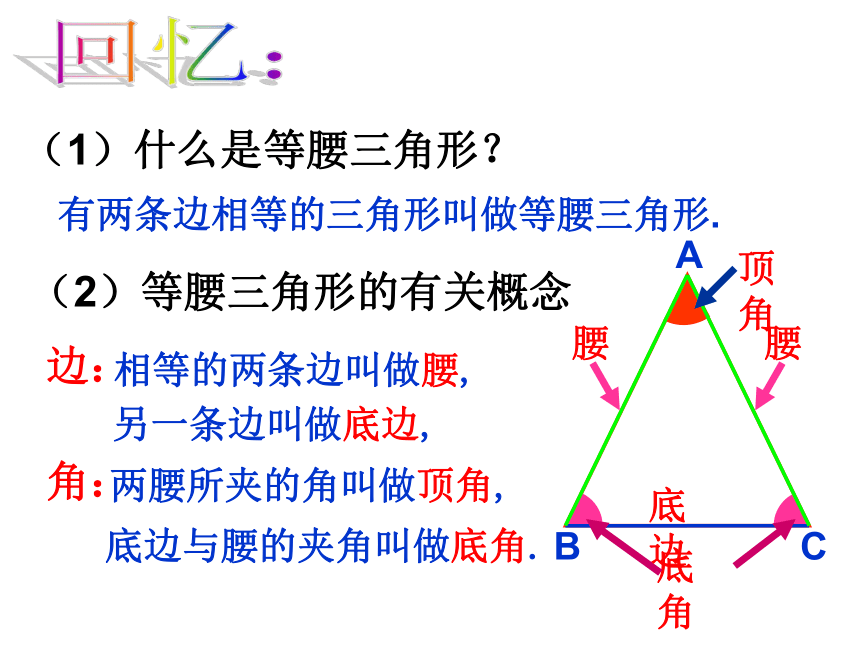
(1)什么是等腰三角形?
(2)等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
回忆:
心灵手巧
相信你:
C
A
B
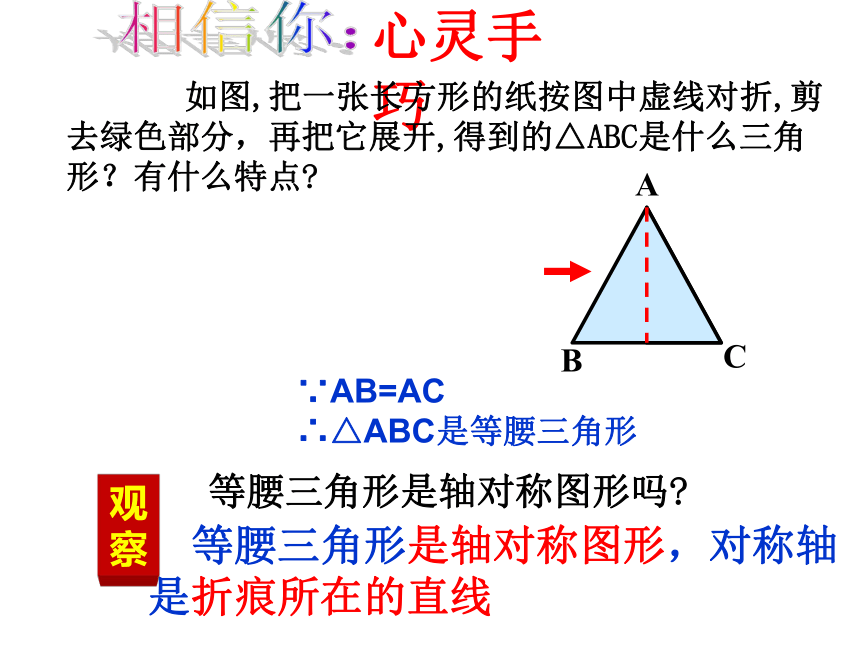
∵AB=AC
∴△ABC是等腰三角形
观察
等腰三角形是轴对称图形吗?
等腰三角形是轴对称图形,对称轴是折痕所在的直线
如图,把一张长方形的纸按图中虚线对折,剪去绿色部分,再把它展开,得到的△ABC是什么三角形?有什么特点?
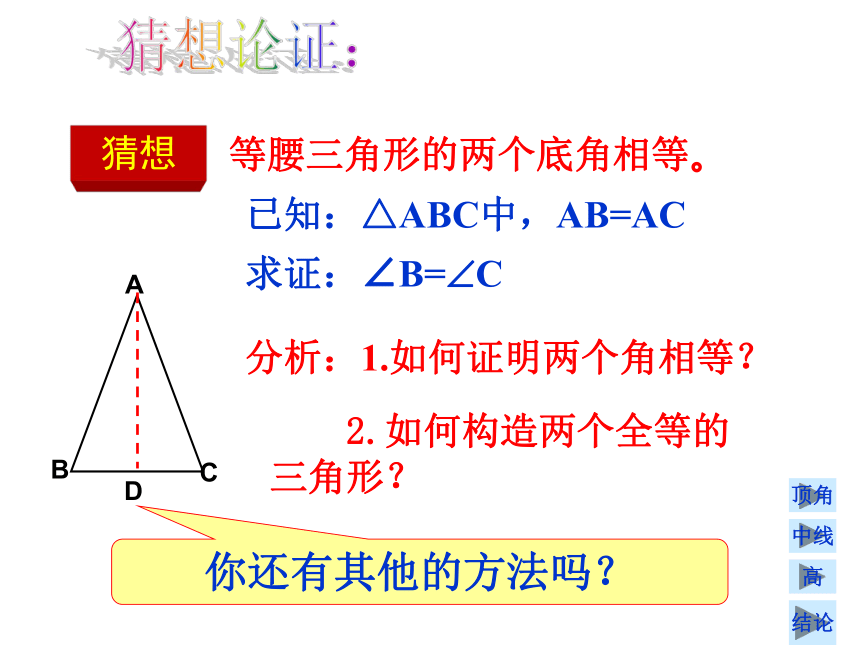
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的 三角形?
猜想
A
B
C
D
猜想论证:
顶角
中线
高
结论
你还有其他的方法吗?
A
B
C
则有∠1=∠2
D
1
2
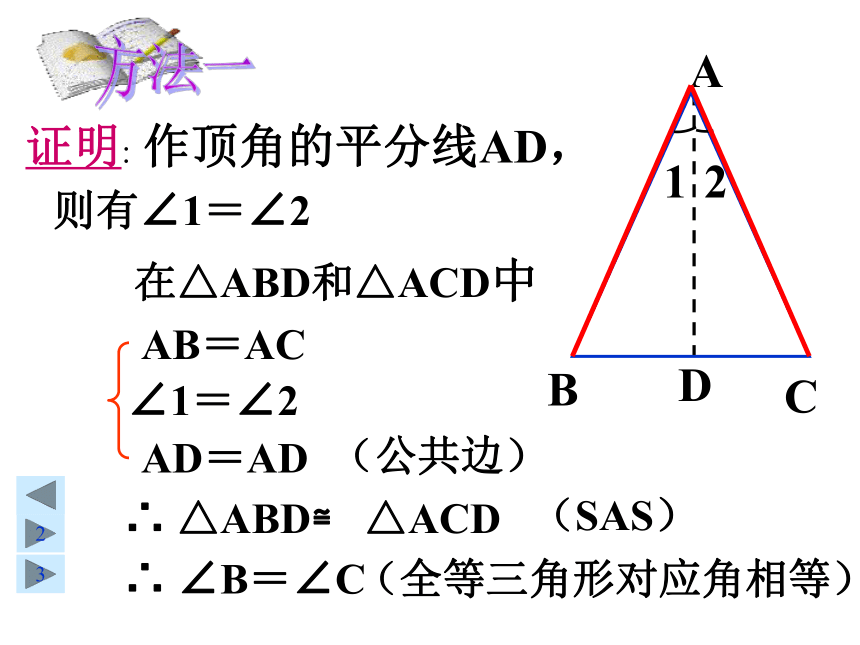
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
2
3
3
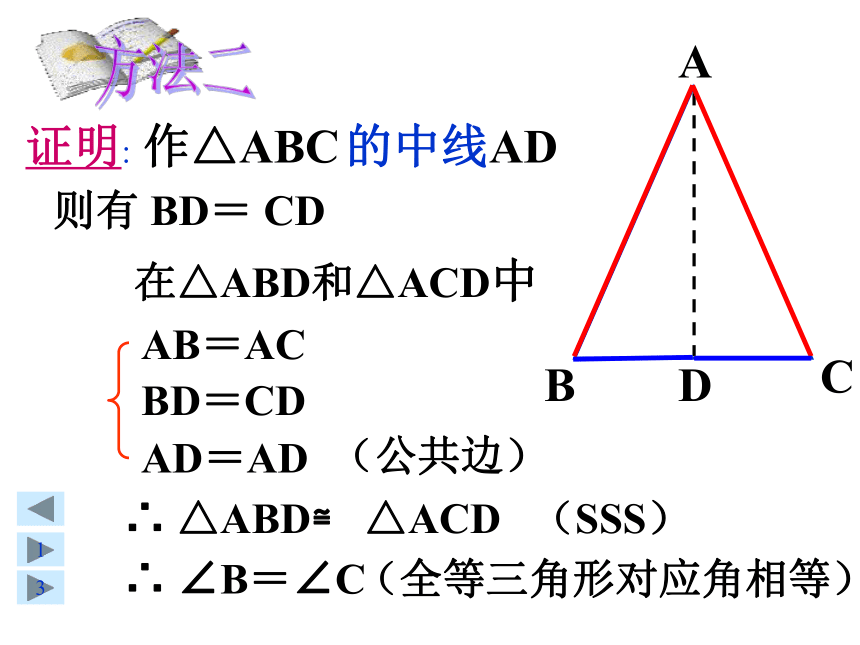
则有 BD= CD
A
B
C
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
3
1
A
B
C
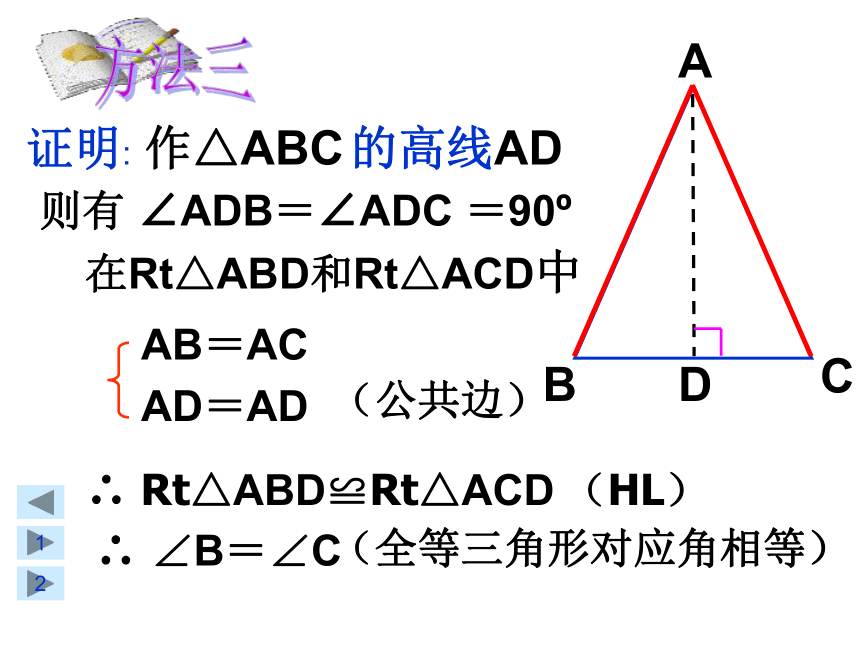
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
方法三
1
2
∴ ∠B =∠C ( )
在△ABC中,
∵ AC = AB( )
已知
等边对等角
C
A
B
性质1:等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:
在 三角形中,等边对等角。
同一个
几何语言:
归纳结论:
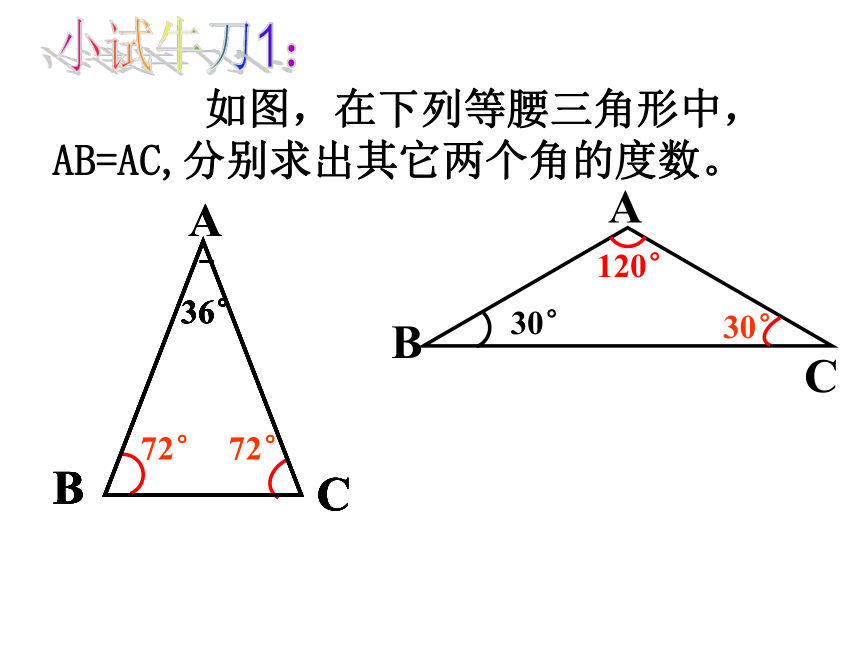
如图,在下列等腰三角形中,AB=AC,分别求出其它两个角的度数。
A
B
C
120°
A
B
C
36°
72°
72°
30°
30°
小试牛刀1:
B
C
36°
B
C
36°
B
C
36°
B
C
36°
A
B
C
36°
⒈等腰三角形一个底角为75°,它的另外两个角为 ;
⒉等腰三角形一个角为70°,它的另外两个角为___________________;
⒊等腰三角形一个角为110°,它的另外两个角为 。
75°, 30°
70°,40°或 55°,55°
35°,35°
小结: 0°<顶角<180°
0°<底角<90°
小试牛刀2:
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
典型例题:
想一想:
等腰三角形的边和角我们已经研究过了,再看看这条折痕AD与△ABC的有什么关系?
B
D
C
猜想:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合
A
A
B
C
则有∠1= ∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ BD=CD
∠ADB =∠ADC=
90°
论证猜想
猜想:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
(简称:三线合一)
性质2:
几何语言:
在△ABC中,AB =AC, 点 D在BC上
1、∵ AB =AC ,AD ⊥ BC
∴∠ = ∠ , = 。
2、∵ AB =AC ,BD=CD,
∴ ⊥ ,∠ =∠ 。
3、∵ AB =AC ,∠1=∠2,
∴ ⊥ , = 。
1
2
1
2
BD
CD
AD
BC
1
2
BC
BD
CD
A
B
D
C
归纳结论:
等腰三角形的对称轴:
顶角的平分线(底边上的中线、底边上的高)所在的直线
或底边上的垂直平分线
AD
用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.
操作尝试:
(1)解:∵AB=AC,BD=DC(已知)
∴∠1= ∠2= ∠BAC(三线合一)
∵ ∠BAC=110°(已知)
∴∠ 1= ∠2= 55°(等式性质)
例 2 如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠1、∠2的度数;
(2) 求证:AD⊥BC .
典型例题:
(2)证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
已知:如图在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF
思考:
通过这节课,
你学到了什么?
已知:如图在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF
D
A
B
C
F
E
思考:
如图,在△ABC中,AB=AC,高CD、BE相交于点P,
求证:AP平分∠BAC
拓展提升:
4°
如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FM、MH……,添加的 钢管长度都与OE相等,添加这样的钢管4根时,则∠AHB 的度数为( )
E
O
F
H
M
B
A
50°
10°
拓展提升:
10°
20°
20°
30°
30°
40°
40°
50°
50°
60°
80°
60°
80°
如图,点D、E在△ABC的边BC上,
且AB=AC,AD=AE,此时BD与CE有何关系?请说明理由。
拓展提升:
如图所示,已知下列两个三角形,思考 怎样把每个三角形只剪一次,将它分成两个 等腰三角形?试一试,你一定会成功的。
120°
20 °
40 °
100 °
20 °
60 °
120°
20 °
40 °
20 °
100 °
20 °
60 °
20 °
思维升级,我最棒
老师寄语:
选择了远方,就要风雨兼程;
选择了大海,就要乘风破浪;
选择了蓝天,就要展翅翱翔。
唤醒你所有的潜能,用信心铸就目标,用汗水浇灌希望,用拼搏实现理想,用奋斗赢得一生!
有两条边相等的三角形叫做等腰三角形.
(1)什么是等腰三角形?
(2)等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
回忆:
心灵手巧
相信你:
C
A
B
∵AB=AC
∴△ABC是等腰三角形
观察
等腰三角形是轴对称图形吗?
等腰三角形是轴对称图形,对称轴是折痕所在的直线
如图,把一张长方形的纸按图中虚线对折,剪去绿色部分,再把它展开,得到的△ABC是什么三角形?有什么特点?
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的 三角形?
猜想
A
B
C
D
猜想论证:
顶角
中线
高
结论
你还有其他的方法吗?
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
2
3
3
则有 BD= CD
A
B
C
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
3
1
A
B
C
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
方法三
1
2
∴ ∠B =∠C ( )
在△ABC中,
∵ AC = AB( )
已知
等边对等角
C
A
B
性质1:等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:
在 三角形中,等边对等角。
同一个
几何语言:
归纳结论:
如图,在下列等腰三角形中,AB=AC,分别求出其它两个角的度数。
A
B
C
120°
A
B
C
36°
72°
72°
30°
30°
小试牛刀1:
B
C
36°
B
C
36°
B
C
36°
B
C
36°
A
B
C
36°
⒈等腰三角形一个底角为75°,它的另外两个角为 ;
⒉等腰三角形一个角为70°,它的另外两个角为___________________;
⒊等腰三角形一个角为110°,它的另外两个角为 。
75°, 30°
70°,40°或 55°,55°
35°,35°
小结: 0°<顶角<180°
0°<底角<90°
小试牛刀2:
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
典型例题:
想一想:
等腰三角形的边和角我们已经研究过了,再看看这条折痕AD与△ABC的有什么关系?
B
D
C
猜想:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合
A
A
B
C
则有∠1= ∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ BD=CD
∠ADB =∠ADC=
90°
论证猜想
猜想:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
(简称:三线合一)
性质2:
几何语言:
在△ABC中,AB =AC, 点 D在BC上
1、∵ AB =AC ,AD ⊥ BC
∴∠ = ∠ , = 。
2、∵ AB =AC ,BD=CD,
∴ ⊥ ,∠ =∠ 。
3、∵ AB =AC ,∠1=∠2,
∴ ⊥ , = 。
1
2
1
2
BD
CD
AD
BC
1
2
BC
BD
CD
A
B
D
C
归纳结论:
等腰三角形的对称轴:
顶角的平分线(底边上的中线、底边上的高)所在的直线
或底边上的垂直平分线
AD
用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.
操作尝试:
(1)解:∵AB=AC,BD=DC(已知)
∴∠1= ∠2= ∠BAC(三线合一)
∵ ∠BAC=110°(已知)
∴∠ 1= ∠2= 55°(等式性质)
例 2 如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠1、∠2的度数;
(2) 求证:AD⊥BC .
典型例题:
(2)证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
已知:如图在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF
思考:
通过这节课,
你学到了什么?
已知:如图在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF
D
A
B
C
F
E
思考:
如图,在△ABC中,AB=AC,高CD、BE相交于点P,
求证:AP平分∠BAC
拓展提升:
4°
如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FM、MH……,添加的 钢管长度都与OE相等,添加这样的钢管4根时,则∠AHB 的度数为( )
E
O
F
H
M
B
A
50°
10°
拓展提升:
10°
20°
20°
30°
30°
40°
40°
50°
50°
60°
80°
60°
80°
如图,点D、E在△ABC的边BC上,
且AB=AC,AD=AE,此时BD与CE有何关系?请说明理由。
拓展提升:
如图所示,已知下列两个三角形,思考 怎样把每个三角形只剪一次,将它分成两个 等腰三角形?试一试,你一定会成功的。
120°
20 °
40 °
100 °
20 °
60 °
120°
20 °
40 °
20 °
100 °
20 °
60 °
20 °
思维升级,我最棒
老师寄语:
选择了远方,就要风雨兼程;
选择了大海,就要乘风破浪;
选择了蓝天,就要展翅翱翔。
唤醒你所有的潜能,用信心铸就目标,用汗水浇灌希望,用拼搏实现理想,用奋斗赢得一生!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
