7.1为什么要证明-北师大版八年级数学上册课件(17张)
文档属性
| 名称 | 7.1为什么要证明-北师大版八年级数学上册课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 15:56:15 | ||
图片预览





文档简介
筷子真的变折了吗?
三角形三条边是直的吗?
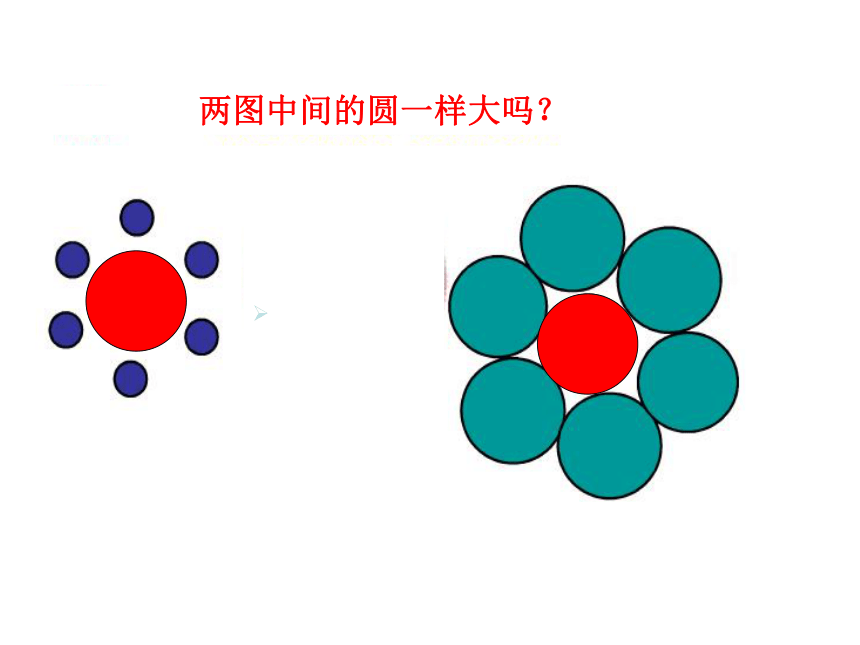
两图中间的圆一样大吗?
第七章 平行线的证明
7.1 为什么要证明
学习目标(1分钟)
1.经历观察、验证、归纳等过程,明确通过观察、猜想得到的结论不一定正确,必须进行推理证明;
2.用实验验证、举出反例、推理等方法简单地说明一个数学结论是否正确。
3通过观察、分析图形,体验推理证明的重要性.
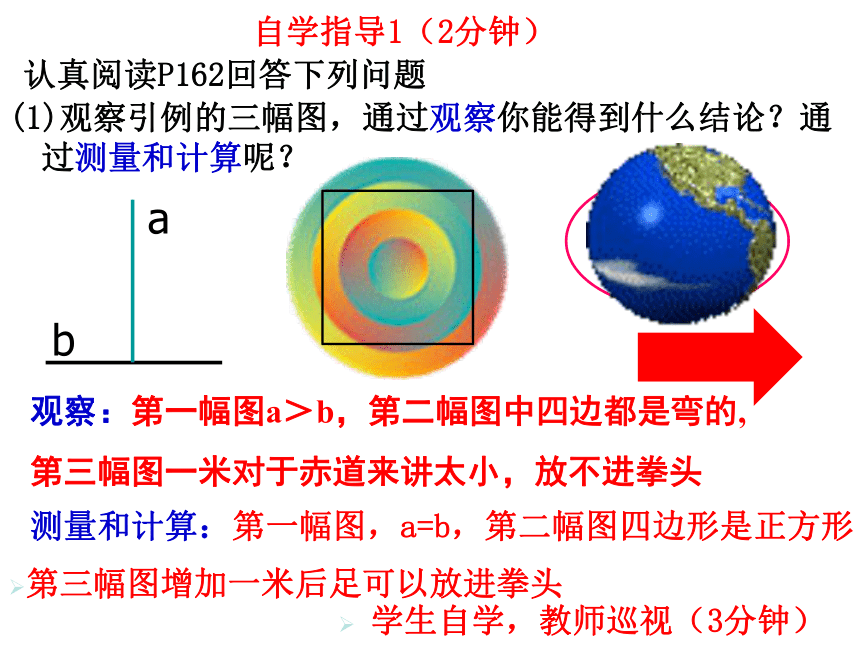
测量和计算:第一幅图,a=b,第二幅图四边形是正方形
自学指导1(2分钟)
认真阅读P162回答下列问题
(1)观察引例的三幅图,通过观察你能得到什么结论?通过测量和计算呢?
学生自学,教师巡视(3分钟)
a
b
第三幅图增加一米后足可以放进拳头
观察:第一幅图a>b,第二幅图中四边都是弯的,
第三幅图一米对于赤道来讲太小,放不进拳头
3.P162图7-4中DE和BC有什么位置和数量关系?
解:错误;当n=11时,代数式的值为121。
解:DE∥BC且DE= BC
1.有人认为,对于所有自然数n,代数式n2-n+11的值都是质数.你认为这个说法正确吗?为什么?
自学检测1(4分钟)
2.P163随堂练习T1
a
b
c
d
实验验证
实验验证
(变式)当n为正整数时,n2+3n+1的值一定是质数吗?
举出反例
解:不一定,当n=6时,n2+3n+1=55=5×11,是一个合数。
阅读P163“议一议”,解决下列问题:
1.____、_____、_____得到的结论可能正确,也可能不正确。因此,要判断一个数学结论是否正确,仅仅依靠实验、观察、归纳是不够的,必须进行有根有据的______。
自学指导2(1分钟)
学生自学,教师巡视(6分钟)
2.看课本P163“读一读”《费马的失误》,并思考费马失误的原因。
实验
观察
归纳
证明
要判断一个结论是否正确,需要有根有据的证明,而费马的结论仅局限于观察和归纳,从而导致失误。
3.检验数学结论是否正确有哪些方法?
2.下列推理正确的是( )
A.弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,因为弟弟的明年比今年长大了1岁
B.如果a>b,b>c,则a>c
C.∠A与∠B相等,原因是它们看起来大小也差不多
D.因为对顶角必然相等,所以相等角也必是对顶角
自学检测2(9分钟)
1.下列说法正确的是( )
A.经验、观察完全可以判断一个数学结论正确与否
B.对于自然数n,n?-n+3一定是质数
C.有7个人,分在6个小组,则至少有2个人在同一组
D.因为对顶角相等,所以相等的角也必是对顶角
c
B
3.我们知道:2×2=4,2+2=4.
试问:对于任意数a与b,是否一定有结论a×b=a+b?
解:不一定,当n=3时,3×3=9≠3+3。
(1分钟)
当堂训练:(15分钟)
A
B
A
4、如图,∠1=60?,∠2=60?,∠3=57?,则∠4=57?,下面是A,B,C,D四个同学的推理过程,你认为推理正确的是( )
A.因为∠1=60?=∠2,所以a∥b,
所以∠4=∠3=57?
B.因为∠4=57?=∠3,所以a∥b,
故∠1=∠2=60?
C.因为∠2=∠5,又∠1=60?,∠2=60?,
故∠1=∠5=60?,所以a∥b,
所以∠4=∠3=57?
D.因为∠1=60?,∠2=60?,∠3=57?,
所以∠1=∠3=∠2-∠4=60?-57?=3?,
故∠4=57?
C
6.下列结论是否正确,若不正确,请举反例说明
(1)如果|x| > |y|, 那么x >y.
(2) 如果|x| > |y|, 那么x2 >y2.
(3) 如果x2 >y2, 那么|x| > |y|.
(4) 如果x >y, 那么|x| > |y|.
(5) 若a<1, 则a2<1
5.已知一个三角形,①最少有两个锐角 ②最多有两个锐角 ③最大角的度数不小于60°④一个三角形中,最少有两个钝角 。其中正确的有几个?( )
A . 1 B. 2 C. 3 D. 4
不正确,如 |-5| > |2|,但是-5<2
正确
正确
B
不正确如0>-2,但|0| < |-2 |
不正确如-3<1,但(-3)2 > 1
选做题
7.小洁、琳琳、晓彤、奇奇和聪聪5位同学身体都不怎么舒服,他们分别在医院的牙科、眼科、皮肤科、外科、耳鼻喉科就诊。请根据他们的对话猜一猜,他们分别去了哪一科看病?
小洁、琳琳、晓彤说:我们是在牙科、眼科和皮肤科各自接受治疗的。
奇奇说:我没有去耳鼻喉科和皮肤科。
晓彤说:我最近夜里牙老疼。
小洁说:我的皮肤好得很,我没有必要去皮肤科。
琳琳看皮肤科
小洁看眼科
晓彤看牙科
奇奇看外科
聪聪看耳鼻喉科
假如用一根比地球赤道长1米的铁丝将地球赤道围起来,那么铁丝与赤道之间的间隙能有多大(把地球看成球形)?能放进一颗红枣吗?能放进一个拳头吗?
解:设赤道的周长为C,则铁丝与地球赤道的间隙为
16cm的间隙不仅能放进一颗红枣,也能放进一个拳头
板书设计
7.1 为什么要证明
1、经历观察、验证、归纳等过程,对一些方法所得的结论产生怀疑,从而认识证明的必要性;
2、掌握检验数学的常用方法:实验验证、举出反例、推理等。
三角形三条边是直的吗?
两图中间的圆一样大吗?
第七章 平行线的证明
7.1 为什么要证明
学习目标(1分钟)
1.经历观察、验证、归纳等过程,明确通过观察、猜想得到的结论不一定正确,必须进行推理证明;
2.用实验验证、举出反例、推理等方法简单地说明一个数学结论是否正确。
3通过观察、分析图形,体验推理证明的重要性.
测量和计算:第一幅图,a=b,第二幅图四边形是正方形
自学指导1(2分钟)
认真阅读P162回答下列问题
(1)观察引例的三幅图,通过观察你能得到什么结论?通过测量和计算呢?
学生自学,教师巡视(3分钟)
a
b
第三幅图增加一米后足可以放进拳头
观察:第一幅图a>b,第二幅图中四边都是弯的,
第三幅图一米对于赤道来讲太小,放不进拳头
3.P162图7-4中DE和BC有什么位置和数量关系?
解:错误;当n=11时,代数式的值为121。
解:DE∥BC且DE= BC
1.有人认为,对于所有自然数n,代数式n2-n+11的值都是质数.你认为这个说法正确吗?为什么?
自学检测1(4分钟)
2.P163随堂练习T1
a
b
c
d
实验验证
实验验证
(变式)当n为正整数时,n2+3n+1的值一定是质数吗?
举出反例
解:不一定,当n=6时,n2+3n+1=55=5×11,是一个合数。
阅读P163“议一议”,解决下列问题:
1.____、_____、_____得到的结论可能正确,也可能不正确。因此,要判断一个数学结论是否正确,仅仅依靠实验、观察、归纳是不够的,必须进行有根有据的______。
自学指导2(1分钟)
学生自学,教师巡视(6分钟)
2.看课本P163“读一读”《费马的失误》,并思考费马失误的原因。
实验
观察
归纳
证明
要判断一个结论是否正确,需要有根有据的证明,而费马的结论仅局限于观察和归纳,从而导致失误。
3.检验数学结论是否正确有哪些方法?
2.下列推理正确的是( )
A.弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,因为弟弟的明年比今年长大了1岁
B.如果a>b,b>c,则a>c
C.∠A与∠B相等,原因是它们看起来大小也差不多
D.因为对顶角必然相等,所以相等角也必是对顶角
自学检测2(9分钟)
1.下列说法正确的是( )
A.经验、观察完全可以判断一个数学结论正确与否
B.对于自然数n,n?-n+3一定是质数
C.有7个人,分在6个小组,则至少有2个人在同一组
D.因为对顶角相等,所以相等的角也必是对顶角
c
B
3.我们知道:2×2=4,2+2=4.
试问:对于任意数a与b,是否一定有结论a×b=a+b?
解:不一定,当n=3时,3×3=9≠3+3。
(1分钟)
当堂训练:(15分钟)
A
B
A
4、如图,∠1=60?,∠2=60?,∠3=57?,则∠4=57?,下面是A,B,C,D四个同学的推理过程,你认为推理正确的是( )
A.因为∠1=60?=∠2,所以a∥b,
所以∠4=∠3=57?
B.因为∠4=57?=∠3,所以a∥b,
故∠1=∠2=60?
C.因为∠2=∠5,又∠1=60?,∠2=60?,
故∠1=∠5=60?,所以a∥b,
所以∠4=∠3=57?
D.因为∠1=60?,∠2=60?,∠3=57?,
所以∠1=∠3=∠2-∠4=60?-57?=3?,
故∠4=57?
C
6.下列结论是否正确,若不正确,请举反例说明
(1)如果|x| > |y|, 那么x >y.
(2) 如果|x| > |y|, 那么x2 >y2.
(3) 如果x2 >y2, 那么|x| > |y|.
(4) 如果x >y, 那么|x| > |y|.
(5) 若a<1, 则a2<1
5.已知一个三角形,①最少有两个锐角 ②最多有两个锐角 ③最大角的度数不小于60°④一个三角形中,最少有两个钝角 。其中正确的有几个?( )
A . 1 B. 2 C. 3 D. 4
不正确,如 |-5| > |2|,但是-5<2
正确
正确
B
不正确如0>-2,但|0| < |-2 |
不正确如-3<1,但(-3)2 > 1
选做题
7.小洁、琳琳、晓彤、奇奇和聪聪5位同学身体都不怎么舒服,他们分别在医院的牙科、眼科、皮肤科、外科、耳鼻喉科就诊。请根据他们的对话猜一猜,他们分别去了哪一科看病?
小洁、琳琳、晓彤说:我们是在牙科、眼科和皮肤科各自接受治疗的。
奇奇说:我没有去耳鼻喉科和皮肤科。
晓彤说:我最近夜里牙老疼。
小洁说:我的皮肤好得很,我没有必要去皮肤科。
琳琳看皮肤科
小洁看眼科
晓彤看牙科
奇奇看外科
聪聪看耳鼻喉科
假如用一根比地球赤道长1米的铁丝将地球赤道围起来,那么铁丝与赤道之间的间隙能有多大(把地球看成球形)?能放进一颗红枣吗?能放进一个拳头吗?
解:设赤道的周长为C,则铁丝与地球赤道的间隙为
16cm的间隙不仅能放进一颗红枣,也能放进一个拳头
板书设计
7.1 为什么要证明
1、经历观察、验证、归纳等过程,对一些方法所得的结论产生怀疑,从而认识证明的必要性;
2、掌握检验数学的常用方法:实验验证、举出反例、推理等。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
