华东师大版八年级数学上册14.1: 直角三角形三边的关系课件(20张)
文档属性
| 名称 | 华东师大版八年级数学上册14.1: 直角三角形三边的关系课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 16:06:00 | ||
图片预览





文档简介
14.1.1直角三角形
三边的关系
施庵镇一初中 岳静
情景导入
1. 探索并掌握勾股定理,学会勾股定理的 简单应用。
2.在经历探索勾股定理过程中,体会类比从特殊到一般的数学思想,并在探索过程中培养归纳、概括能力。
3.通过探索直角三角形的三边之间关系,培养学生积极参与、合作交流的意识。
学习目标:
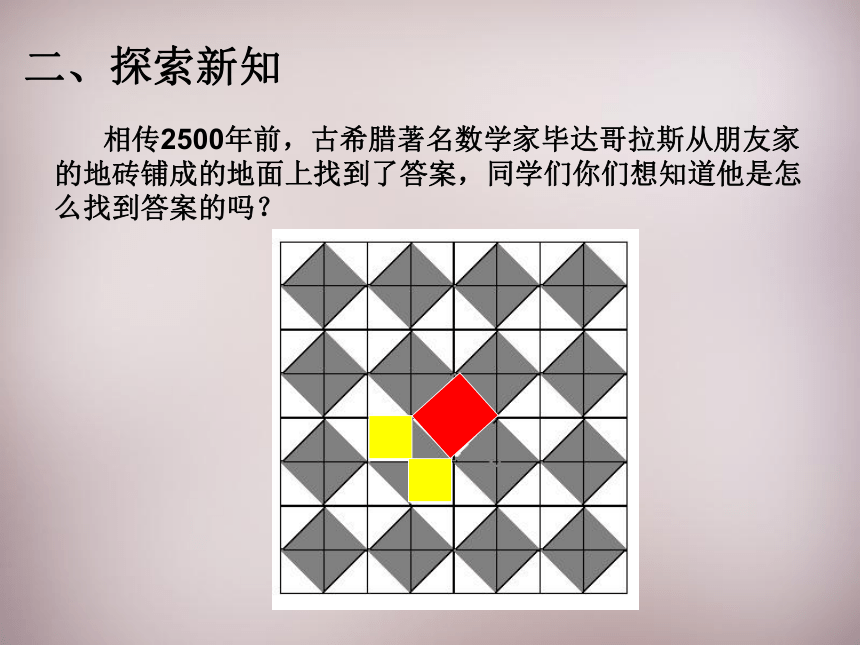
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们你们想知道他是怎么找到答案的吗?
二、探索新知
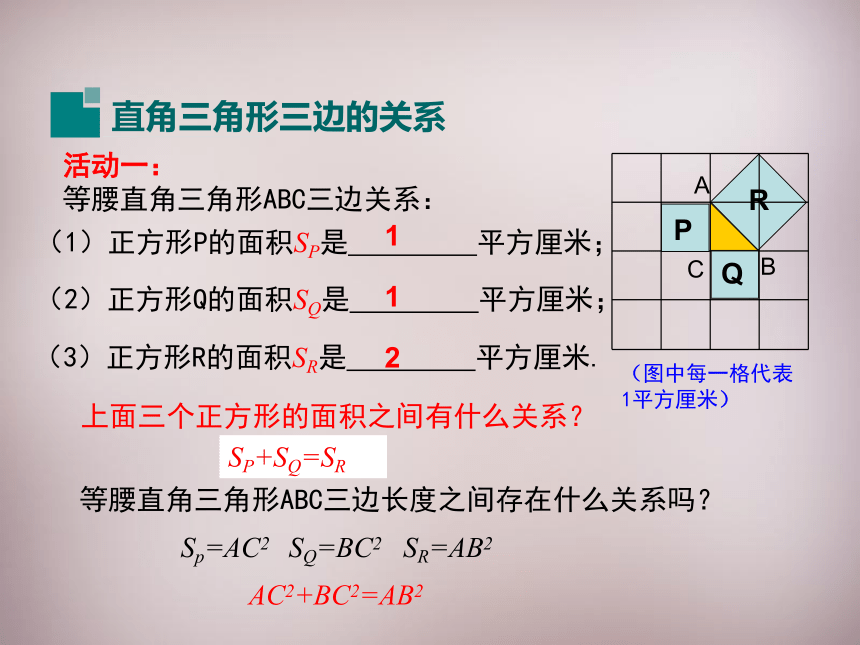
(图中每一格代表1平方厘米)
(1)正方形P的面积SP是 平方厘米;
(2)正方形Q的面积SQ是 平方厘米;
(3)正方形R的面积SR是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
直角三角形三边的关系
上面三个正方形的面积之间有什么关系?
活动一:
等腰直角三角形ABC三边关系:
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
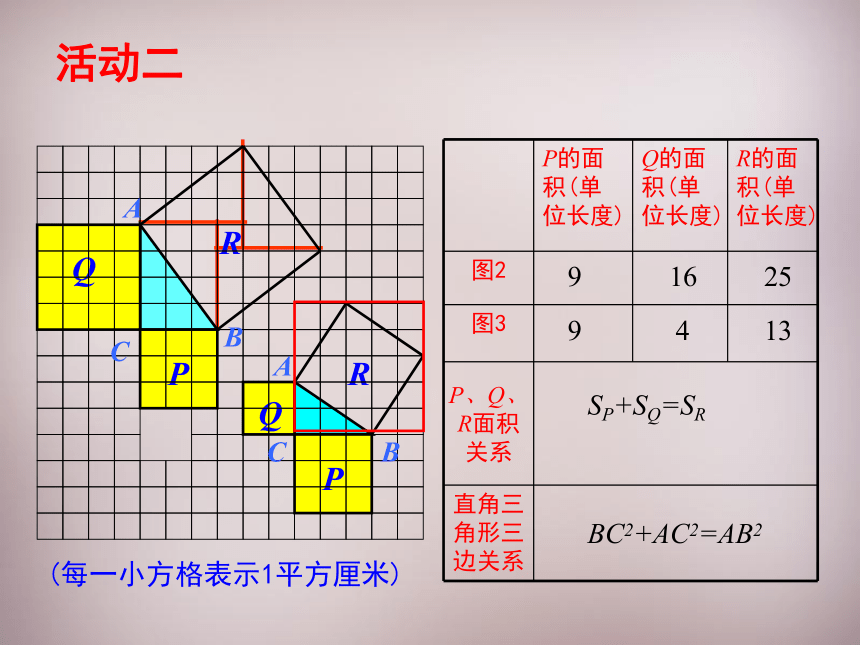
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
想一想
P的面积(单位长度)
Q的面积(单位长度)
R的面积(单位长度)
图2
图3
P、Q、R面积关系
直角三角形三边关系
Q
P
R
Q
P
R
A
B
C
A
B
C
9
16
25
9
4
13
SP+SQ=SR
(每一小方格表示1平方厘米)
BC2+AC2=AB2
活动二
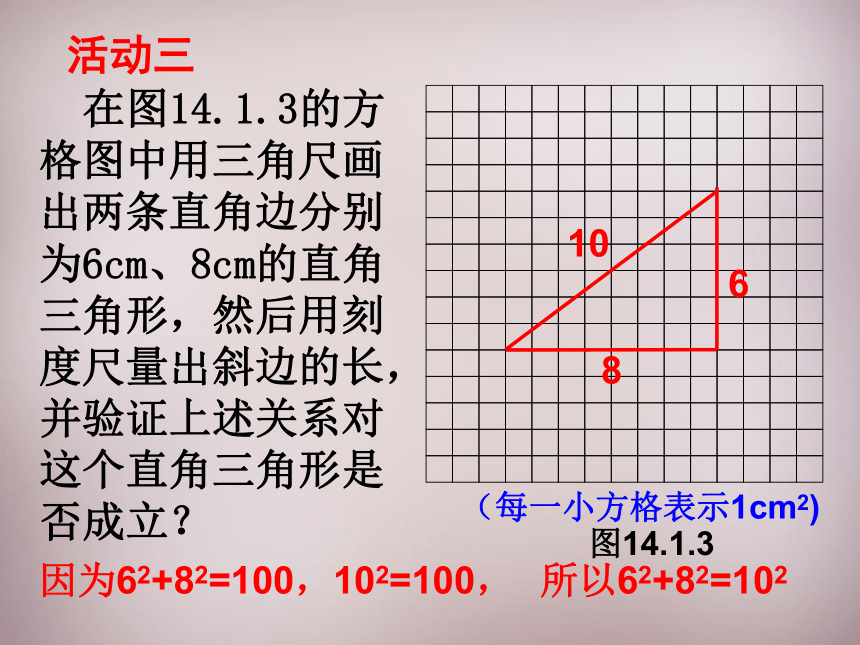
活动三
在图14.1.3的方格图中用三角尺画出两条直角边分别为6cm、8cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立?
(每一小方格表示1cm2)
图14.1.3
6
8
10
因为62+82=100,102=100,
所以62+82=102
由前面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有 a2+b2=c2
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
归 纳
勾股定理揭示了直角三角形三边之间的关系.
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
公式变形
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
c
a
b
勾
股
弦
关于勾股定理:
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
温馨提示:上述这种验证勾股定理的方法是用面积法
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
a
b
c
S大正方形=c2
S小正方形=(b-a)2
赵爽弦图
证明:
b-a
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4?
∵ (a+b)2 = c2 + 4?
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
做一做
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
求下列图形中未知正方形的面积或未知边的长度(口答):
已知直角三角形两边,求第三边.
练一练
2.判断题 ①△ABC的两边AB=5,AC=12,则BC=13 ( ) ②△ABC的a=6,b=8,则c=10 ( )
3.填空题 在△ABC中, ∠C=90°,AC=6,CB=8,则△ABC面积为_____,斜边为上的高为______.
?
?
24
4.8
A
B
C
D
当堂练习
1.图中阴影部分是一个正方形,则此正方形的面积
为 .
4cm
5 cm
9 cm?
4.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7.
课堂小结
1.谈谈你这节课的收获与感受;
2.你还有什么困惑?
三边的关系
施庵镇一初中 岳静
情景导入
1. 探索并掌握勾股定理,学会勾股定理的 简单应用。
2.在经历探索勾股定理过程中,体会类比从特殊到一般的数学思想,并在探索过程中培养归纳、概括能力。
3.通过探索直角三角形的三边之间关系,培养学生积极参与、合作交流的意识。
学习目标:
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们你们想知道他是怎么找到答案的吗?
二、探索新知
(图中每一格代表1平方厘米)
(1)正方形P的面积SP是 平方厘米;
(2)正方形Q的面积SQ是 平方厘米;
(3)正方形R的面积SR是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
直角三角形三边的关系
上面三个正方形的面积之间有什么关系?
活动一:
等腰直角三角形ABC三边关系:
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
想一想
P的面积(单位长度)
Q的面积(单位长度)
R的面积(单位长度)
图2
图3
P、Q、R面积关系
直角三角形三边关系
Q
P
R
Q
P
R
A
B
C
A
B
C
9
16
25
9
4
13
SP+SQ=SR
(每一小方格表示1平方厘米)
BC2+AC2=AB2
活动二
活动三
在图14.1.3的方格图中用三角尺画出两条直角边分别为6cm、8cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立?
(每一小方格表示1cm2)
图14.1.3
6
8
10
因为62+82=100,102=100,
所以62+82=102
由前面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有 a2+b2=c2
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
归 纳
勾股定理揭示了直角三角形三边之间的关系.
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
公式变形
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
c
a
b
勾
股
弦
关于勾股定理:
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
温馨提示:上述这种验证勾股定理的方法是用面积法
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
a
b
c
S大正方形=c2
S小正方形=(b-a)2
赵爽弦图
证明:
b-a
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4?
∵ (a+b)2 = c2 + 4?
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
做一做
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
求下列图形中未知正方形的面积或未知边的长度(口答):
已知直角三角形两边,求第三边.
练一练
2.判断题 ①△ABC的两边AB=5,AC=12,则BC=13 ( ) ②△ABC的a=6,b=8,则c=10 ( )
3.填空题 在△ABC中, ∠C=90°,AC=6,CB=8,则△ABC面积为_____,斜边为上的高为______.
?
?
24
4.8
A
B
C
D
当堂练习
1.图中阴影部分是一个正方形,则此正方形的面积
为 .
4cm
5 cm
9 cm?
4.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7.
课堂小结
1.谈谈你这节课的收获与感受;
2.你还有什么困惑?
