人教版数学八年级上册课件:11.2.1三角形的内角(21张)
文档属性
| 名称 | 人教版数学八年级上册课件:11.2.1三角形的内角(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 388.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 16:22:01 | ||
图片预览






文档简介
温故知新:
(1)AD⊥BC,垂足为D,则AD是________的高,∠_______=∠_______=90°.
(2)AE平分∠BAC,交BC于E点,则AE叫做△ABC的______,∠_____=∠_____=______.
(3)若AF=FC,则△ABC的中线是________,S△ABF=________.
(4)若BG=GH=HF,则AG是________的中线,AH是________的中线.
BC
ADB
ADC
角平分线
BAE
CAE
∠BAC
BF
S△BCF
BH
GF
1、(1)如右图,两直线平行,图中这8个角之间存在怎样的关系?
(2)复行线的性质是什么?
2、(1)直角=_____°;(2)平角=_____°;
(3)周角=________°.
①两直线平行,内错角相等;
②两直线平行,同位角相等;
③两直线平行,同旁内角互补.
90
180
360
3、怎么理解:互余和互补?
11.2.1
三角形的内角
学习目标
1.
掌握三角形内角和定理。
2.会灵活运用三角形内角和定理进行计算和证明。
自学指导
看课本P.11-12的内容,要求:
尝试证明:
证明:三角形内角和等于180°
想一想
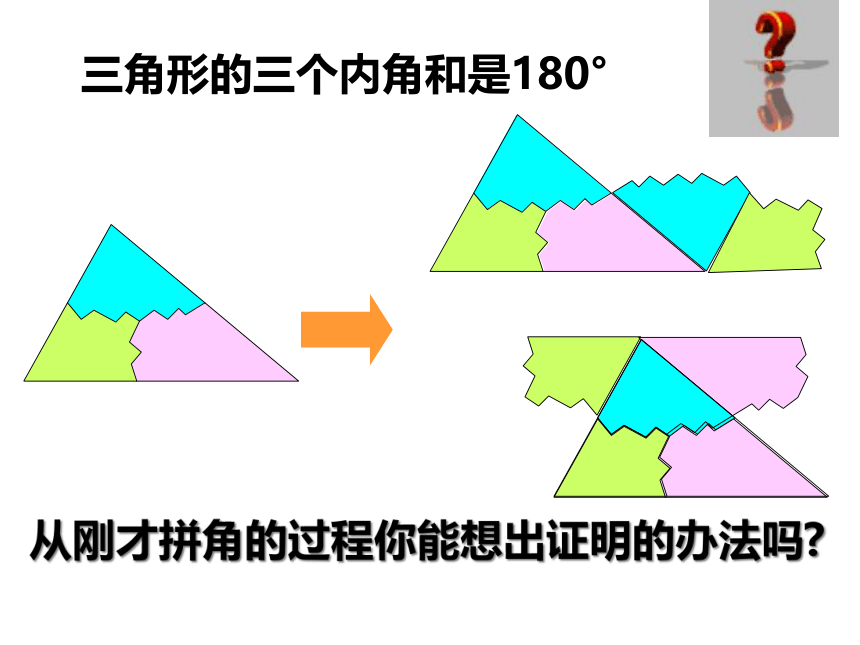
三角形的三个内角和是多少?
把三个角拼在一起试试看?
你有什么办法可以验证呢?
180°
三角形的三个内角和是180°
从刚才拼角的过程你能想出证明的办法吗?
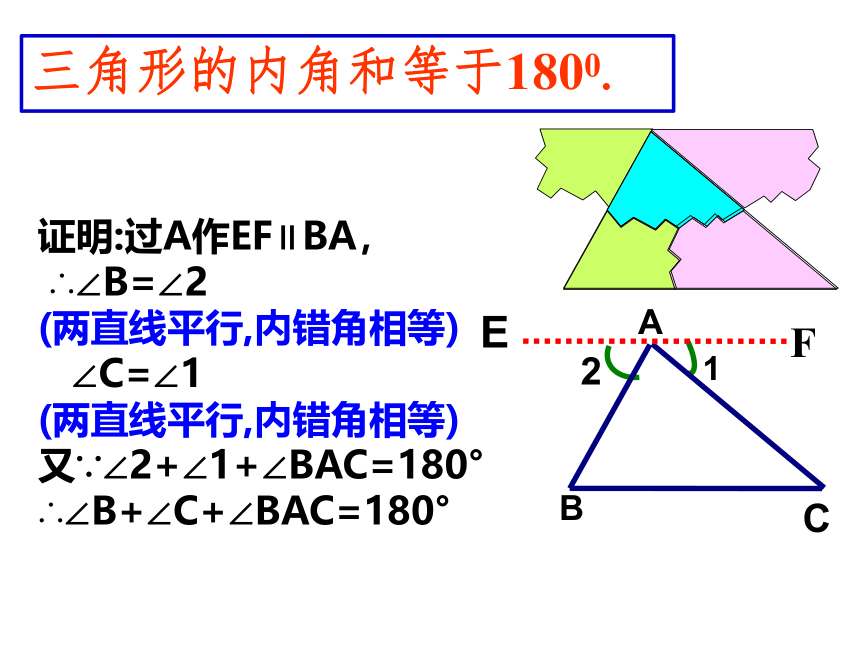
证明:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
三角形的内角和等于1800.
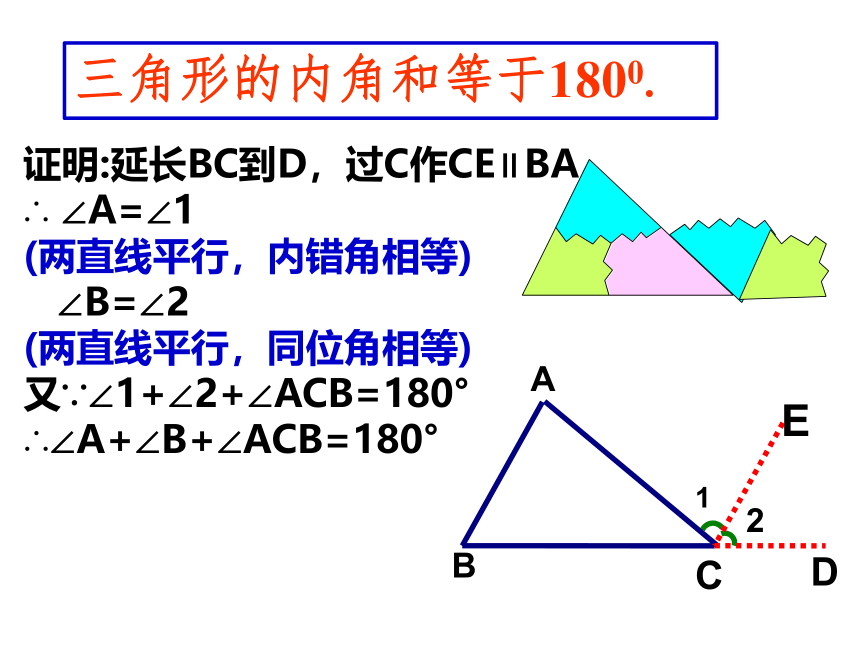
证明:延长BC到D,过C作CE∥BA,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
证明:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
C
B
E
A
三角形的内角和等于1800.
思路总结
为了证明三个角的和为180°,利用逆向思考的方法,把问题转化为一个平角,同旁内角互补,或者两个直角之和,或者其它方法.这种转化思想是数学中的常用方法.
例1:在△ABC中,∠A=80°,∠B=∠C
,
求∠C的度数。
解:∵在△ABC中,∠A=80°
∠A+∠B+∠C=180°,
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
A
B
C
例2:已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
由三角形内角和为180°得
x+3x+5x=180°
解得
x=20°
所以三个内角度数分别为20°,60°,100°。
x+3x+5x=180°
解得
x=20°
解:设三个内角度数分别为:
x、3x、5x,
例3:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
北
.
A
D
北
.
C
B
.
东
E
50°
40°
80°
(1)在△ABC中,∠A=35°,∠B=43°
则∠C=
.
(2)在△ABC中,∠A
:∠B:∠C=2:3:4,
则∠A
=
,∠B=
,
∠C=
.
(3)在△ABC中,∠A=55°,
∠B=43
°,则∠ACB=
∠ACD=
102°
80°
60°
40°
新知应用
B
A
C
D
82°
98°
________
________
(1)一个三角形中最多有
个直角?
为什么?
(2)一个三角形中最多有
个钝角?
为什么?
(3)一个三角形中至少有
个锐角?
为什么?
(4)任意一个三角形中,最大的一个角
的度数至少为
.
60°
2
1
1
讨论
1
三角形中最大的角是锐角,那么这个三角形是锐角三角形。(
)
2
一个三角形中最多只有一个钝角或直角(
)
3
一个等腰三角形一定是锐角三角形(
)
判断正误
√
√
×
4.如图,
在△ABC中,
BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
5.如图,
在△ABC中,
延长BC至D,
BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E
与∠A的关系,并说明理由.
这节课你有那些收获?
今天作业:
习题11.2
第1、3、4题
(1)AD⊥BC,垂足为D,则AD是________的高,∠_______=∠_______=90°.
(2)AE平分∠BAC,交BC于E点,则AE叫做△ABC的______,∠_____=∠_____=______.
(3)若AF=FC,则△ABC的中线是________,S△ABF=________.
(4)若BG=GH=HF,则AG是________的中线,AH是________的中线.
BC
ADB
ADC
角平分线
BAE
CAE
∠BAC
BF
S△BCF
BH
GF
1、(1)如右图,两直线平行,图中这8个角之间存在怎样的关系?
(2)复行线的性质是什么?
2、(1)直角=_____°;(2)平角=_____°;
(3)周角=________°.
①两直线平行,内错角相等;
②两直线平行,同位角相等;
③两直线平行,同旁内角互补.
90
180
360
3、怎么理解:互余和互补?
11.2.1
三角形的内角
学习目标
1.
掌握三角形内角和定理。
2.会灵活运用三角形内角和定理进行计算和证明。
自学指导
看课本P.11-12的内容,要求:
尝试证明:
证明:三角形内角和等于180°
想一想
三角形的三个内角和是多少?
把三个角拼在一起试试看?
你有什么办法可以验证呢?
180°
三角形的三个内角和是180°
从刚才拼角的过程你能想出证明的办法吗?
证明:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
三角形的内角和等于1800.
证明:延长BC到D,过C作CE∥BA,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
证明:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
C
B
E
A
三角形的内角和等于1800.
思路总结
为了证明三个角的和为180°,利用逆向思考的方法,把问题转化为一个平角,同旁内角互补,或者两个直角之和,或者其它方法.这种转化思想是数学中的常用方法.
例1:在△ABC中,∠A=80°,∠B=∠C
,
求∠C的度数。
解:∵在△ABC中,∠A=80°
∠A+∠B+∠C=180°,
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
A
B
C
例2:已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
由三角形内角和为180°得
x+3x+5x=180°
解得
x=20°
所以三个内角度数分别为20°,60°,100°。
x+3x+5x=180°
解得
x=20°
解:设三个内角度数分别为:
x、3x、5x,
例3:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
北
.
A
D
北
.
C
B
.
东
E
50°
40°
80°
(1)在△ABC中,∠A=35°,∠B=43°
则∠C=
.
(2)在△ABC中,∠A
:∠B:∠C=2:3:4,
则∠A
=
,∠B=
,
∠C=
.
(3)在△ABC中,∠A=55°,
∠B=43
°,则∠ACB=
∠ACD=
102°
80°
60°
40°
新知应用
B
A
C
D
82°
98°
________
________
(1)一个三角形中最多有
个直角?
为什么?
(2)一个三角形中最多有
个钝角?
为什么?
(3)一个三角形中至少有
个锐角?
为什么?
(4)任意一个三角形中,最大的一个角
的度数至少为
.
60°
2
1
1
讨论
1
三角形中最大的角是锐角,那么这个三角形是锐角三角形。(
)
2
一个三角形中最多只有一个钝角或直角(
)
3
一个等腰三角形一定是锐角三角形(
)
判断正误
√
√
×
4.如图,
在△ABC中,
BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
5.如图,
在△ABC中,
延长BC至D,
BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E
与∠A的关系,并说明理由.
这节课你有那些收获?
今天作业:
习题11.2
第1、3、4题
