北师大版九年级数学下册 1.1锐角三角函数课件(共20张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 1.1锐角三角函数课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 657.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览






文档简介
九下第一章
《直角三角形的边角关系》
1.1.1锐角三角函数
比较:
两个梯子哪个更陡?
引入新课
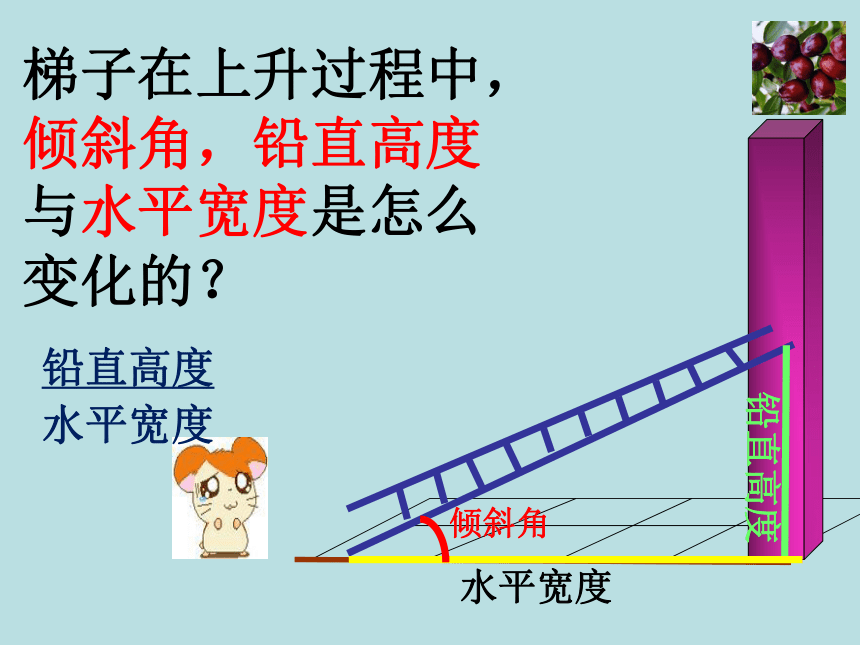
梯子在上升过程中,倾斜角,铅直高度与水平宽度是怎么变化的?
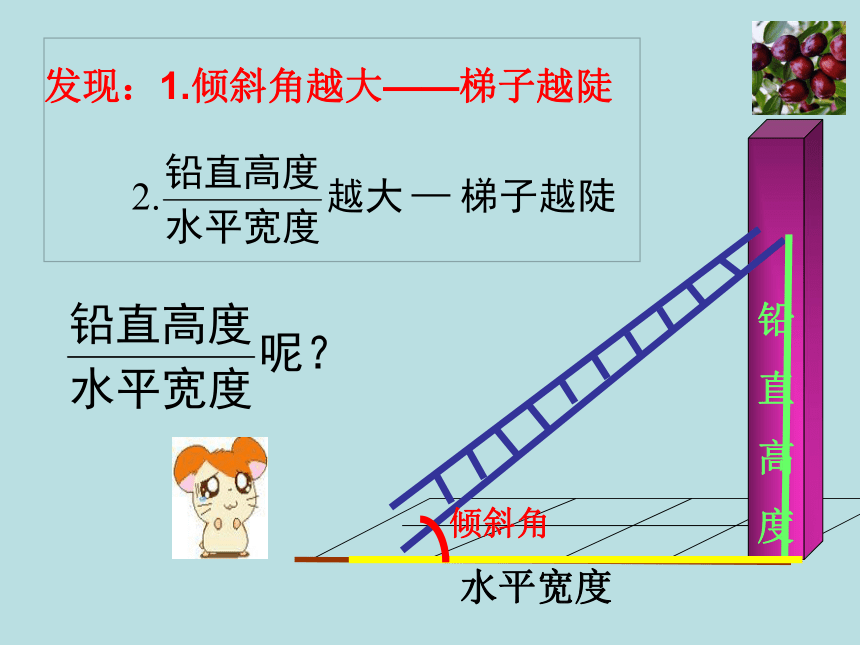
水平宽度
倾斜角
铅直高度
水平宽度
铅直高度
水平宽度
倾斜角
铅
直
高
度
发现:1.倾斜角越大——梯子越陡
A
B
C
∠A的邻边
正切的定义
在Rt△ABC中如果,锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.
记作:tanA
读?
∠A的对边
是个比值,
没有单位
A
B
C
∠A的邻边
正切的定义
∠A的对边
结论:角度越大,
tanA的值越大,
梯子越陡.
C
A
B
tanA的值会变吗?
正切除了表示梯子的倾斜程度外,还经常用来表示坡度
坡角
:坡面与水平面的夹角,记作 α .
2. 坡度 (或坡比)
坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),
记作i, 即 i = h : l .
α
l
h
i= h : l
坡面
水平面
概念类比
结论:坡比越大,i 的值越大,坡面越陡.
1.如图,在Rt△ABC中,∠C=90°.
(1)斜边= ;
(2)∠B的对边= ;
(3)∠B的邻边= ;
(4)
c
b
a
2. 在Rt△ABC中,AC=2,BC=1,则tan A= .
基础巩固练习
直角三角形中,锐角大小确定后,对应的对边和邻边的比值也就确定了
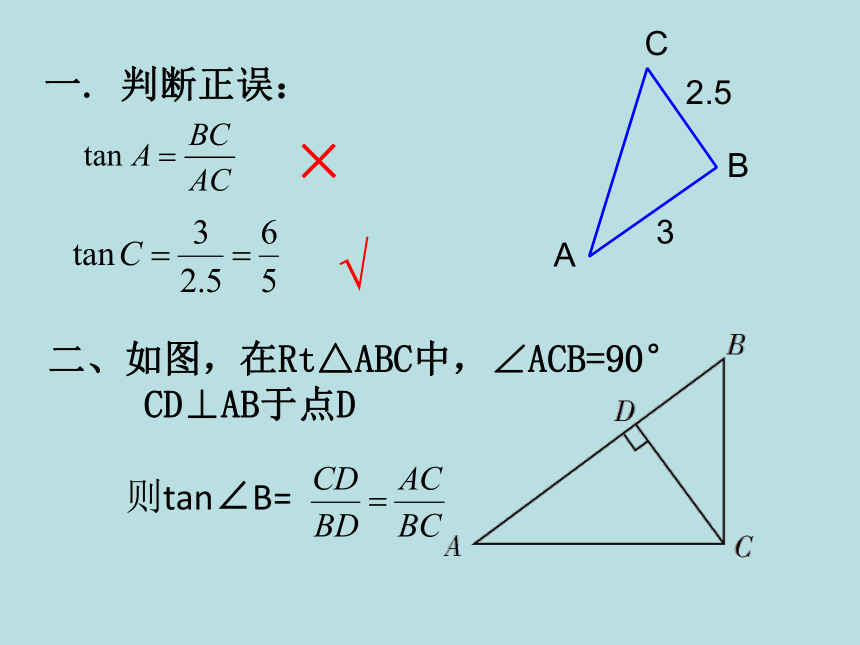
一. 判断正误:
A
C
B
2.5
3
√
×
二、如图,在Rt△ABC中,∠ACB=90°
CD⊥AB于点D
则tan∠B=
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比
(注意顺序: ).
定义的几点说明:
1. (1)在Rt△ABC中,∠A=90°,AC=5,BC=13,则tan∠ABC= .
(2)若菱形ABCD的对角线AC=6,BD=8,则
tan∠ABD= .
练习
(3)如图,在Rt△ABC中,锐角A的对边和邻边同时扩大25倍,tanA的值( )
A.扩大25倍 B.缩小25倍
C.不变 D.不能确定
A
C
B
2. 如图,梯子(长度不变)和地面所成的锐角为∠α . 关于∠α的正切值与梯子的倾斜程度的关系,下列叙述正确的是( )
A. tan α的值越大,梯子越缓
B. tan α的值越小,梯子越陡
C. tan α的值越大,梯子越陡
D. 梯子的倾斜程度与∠α的正切值无关
C
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
B
C
A
3
6
3.在Rt△ABC中,∠C=90°,
(1)如图,AC=3,B=6,求tanA和tanB;
变式: 在Rt△ABC中,∠C=90°,
(2)如图,BC=3,tanA= ,求AC和AB.
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
A
C
B
3
4. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
D
如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A的值为( )
A. B. C. D.
B
类 比 精 练
5. 如图,在△ABC中,AB=AC=5, BC=8. 若∠BPC= ∠BAC,则tan∠BPC=______.
6. 如图所示,某公园入口处原有三级台阶,每级台阶高为18 cm,宽为30 cm. 为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C. 现设计斜坡BC的坡度为1∶5,则AC的长度是 cm.
210
回顾,反思,深化
小结 拓展
1.正切的定义:
Rt△ABC中,锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即
cotA=
A
B
C
∠A
的
对
边
∠A的邻边
┌
Rt△ABC中,锐角A的对边与邻边的比叫做
∠A的正切,记作tanA,即
tanA=
2.余切的定义:正切的倒数叫做∠A的余切,即
请大家谈一谈收获
再见
《直角三角形的边角关系》
1.1.1锐角三角函数
比较:
两个梯子哪个更陡?
引入新课
梯子在上升过程中,倾斜角,铅直高度与水平宽度是怎么变化的?
水平宽度
倾斜角
铅直高度
水平宽度
铅直高度
水平宽度
倾斜角
铅
直
高
度
发现:1.倾斜角越大——梯子越陡
A
B
C
∠A的邻边
正切的定义
在Rt△ABC中如果,锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.
记作:tanA
读?
∠A的对边
是个比值,
没有单位
A
B
C
∠A的邻边
正切的定义
∠A的对边
结论:角度越大,
tanA的值越大,
梯子越陡.
C
A
B
tanA的值会变吗?
正切除了表示梯子的倾斜程度外,还经常用来表示坡度
坡角
:坡面与水平面的夹角,记作 α .
2. 坡度 (或坡比)
坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),
记作i, 即 i = h : l .
α
l
h
i= h : l
坡面
水平面
概念类比
结论:坡比越大,i 的值越大,坡面越陡.
1.如图,在Rt△ABC中,∠C=90°.
(1)斜边= ;
(2)∠B的对边= ;
(3)∠B的邻边= ;
(4)
c
b
a
2. 在Rt△ABC中,AC=2,BC=1,则tan A= .
基础巩固练习
直角三角形中,锐角大小确定后,对应的对边和邻边的比值也就确定了
一. 判断正误:
A
C
B
2.5
3
√
×
二、如图,在Rt△ABC中,∠ACB=90°
CD⊥AB于点D
则tan∠B=
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比
(注意顺序: ).
定义的几点说明:
1. (1)在Rt△ABC中,∠A=90°,AC=5,BC=13,则tan∠ABC= .
(2)若菱形ABCD的对角线AC=6,BD=8,则
tan∠ABD= .
练习
(3)如图,在Rt△ABC中,锐角A的对边和邻边同时扩大25倍,tanA的值( )
A.扩大25倍 B.缩小25倍
C.不变 D.不能确定
A
C
B
2. 如图,梯子(长度不变)和地面所成的锐角为∠α . 关于∠α的正切值与梯子的倾斜程度的关系,下列叙述正确的是( )
A. tan α的值越大,梯子越缓
B. tan α的值越小,梯子越陡
C. tan α的值越大,梯子越陡
D. 梯子的倾斜程度与∠α的正切值无关
C
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
B
C
A
3
6
3.在Rt△ABC中,∠C=90°,
(1)如图,AC=3,B=6,求tanA和tanB;
变式: 在Rt△ABC中,∠C=90°,
(2)如图,BC=3,tanA= ,求AC和AB.
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
A
C
B
3
4. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
D
如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A的值为( )
A. B. C. D.
B
类 比 精 练
5. 如图,在△ABC中,AB=AC=5, BC=8. 若∠BPC= ∠BAC,则tan∠BPC=______.
6. 如图所示,某公园入口处原有三级台阶,每级台阶高为18 cm,宽为30 cm. 为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C. 现设计斜坡BC的坡度为1∶5,则AC的长度是 cm.
210
回顾,反思,深化
小结 拓展
1.正切的定义:
Rt△ABC中,锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即
cotA=
A
B
C
∠A
的
对
边
∠A的邻边
┌
Rt△ABC中,锐角A的对边与邻边的比叫做
∠A的正切,记作tanA,即
tanA=
2.余切的定义:正切的倒数叫做∠A的余切,即
请大家谈一谈收获
再见
