北师大版九年级数学下册第1章第2节特殊角的三角函数值(共24张PPT)
文档属性
| 名称 | 北师大版九年级数学下册第1章第2节特殊角的三角函数值(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 928.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 13:48:18 | ||
图片预览




文档简介
特殊角三角函数值
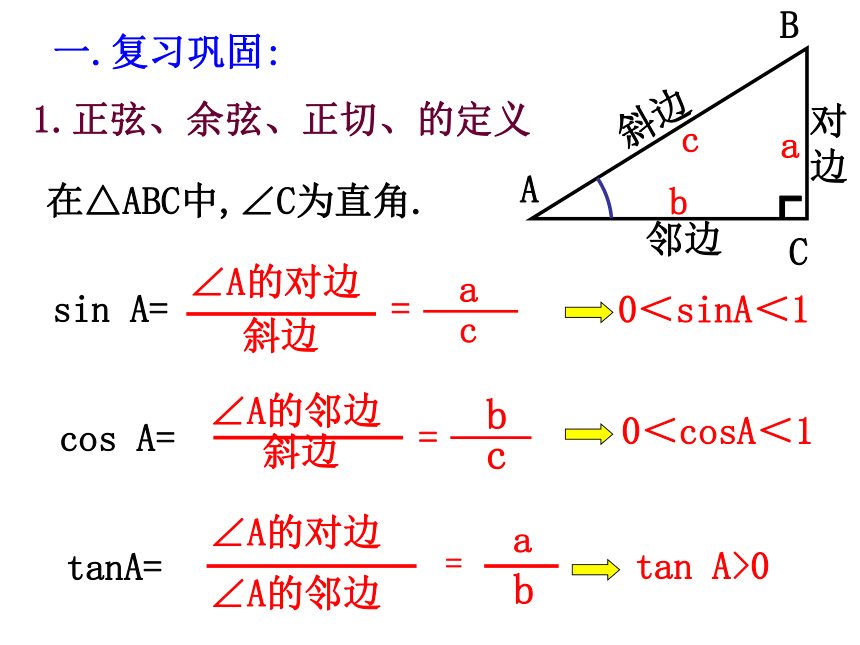
cos A=
1.正弦、余弦、正切、的定义
A
c
b
a
C
B
对边
邻边
斜边
┓
在△ABC中,∠C为直角.
∠A的对边
斜边
a
c
∠A的邻边
斜边
b
c
0<sinA<1
0<cosA<1
sin A=
tanA=
∠A的对边
∠A的邻边
=
a
b
=
=
tan A>0
一.复习巩固:
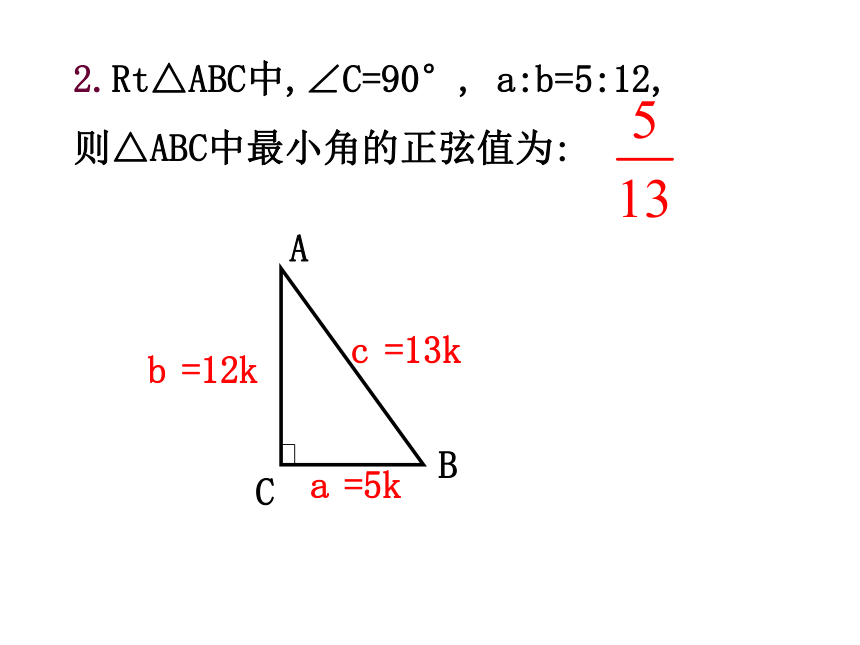
2.Rt△ABC中,∠C=90°, a:b=5:12,
则△ABC中最小角的正弦值为:
A
B
C
a
=5k
c
=13k
b
=12k
3.判断
(1)锐角β的正弦、余弦的值都不小于1.( )
(2)在△ABC中,∠C=90°,若各边长都扩大10倍,则锐角A的正弦值也扩大10倍. ( )
×
×
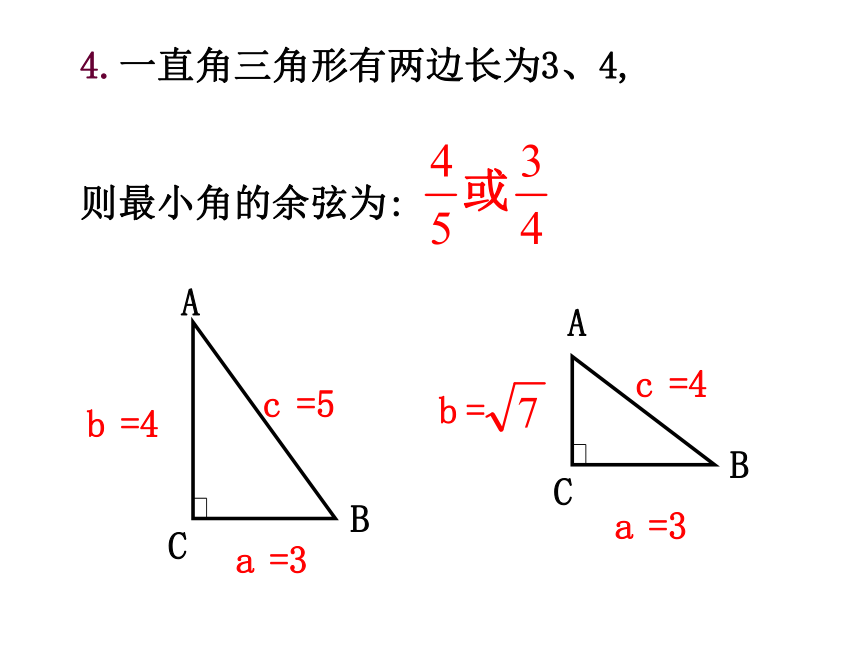
4.一直角三角形有两边长为3、4,
则最小角的余弦为:
A
B
C
a
=3
c
=5
b
=4
A
B
C
a
=3
c
=4
=
b
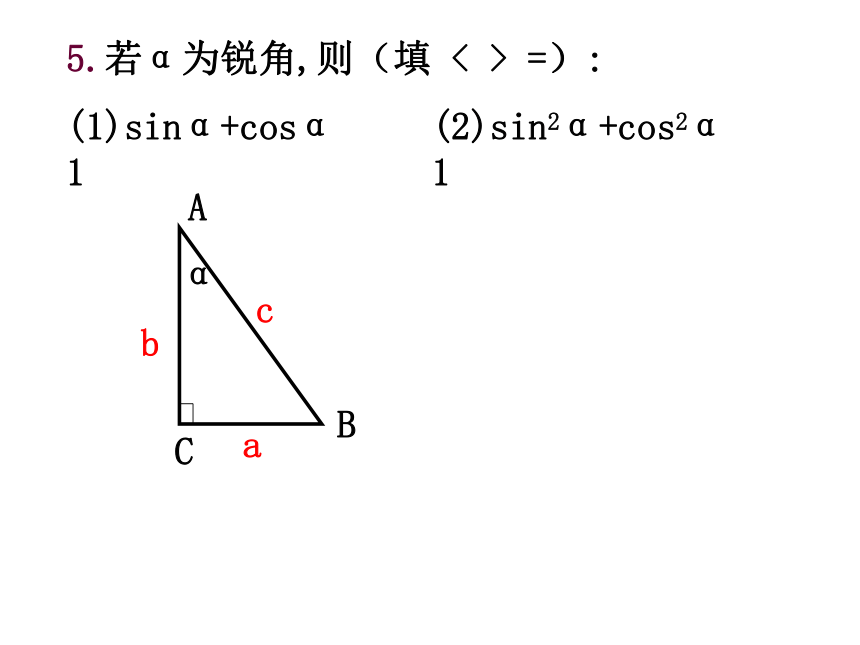
5.若α为锐角,则(填 < > =):
(1)sinα+cosα 1
(2)sin2α+cos2α 1
A
B
C
a
c
b
α
探索与发现
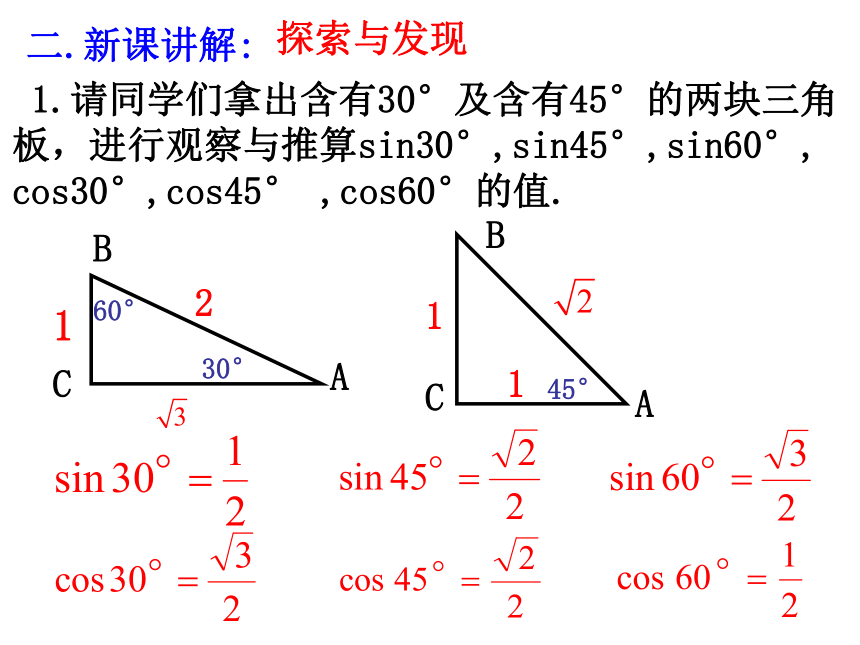
1.请同学们拿出含有30°及含有45°的两块三角板,进行观察与推算sin30°,sin45°,sin60°, cos30°,cos45° ,cos60°的值.
45°
30°
C
C
B
B
A
A
1
1
2
1
60°
二.新课讲解:
探索与发现
45°
30°
C
C
B
B
A
A
k
k
2k
k
60°
二.新课讲解:
1.请同学们拿出含有30°及含有45°的两块三角板,进行观察与推算sin30°,sin45°,sin60°, cos30°,cos45° ,cos60°的值.
2.填表:
α
30°
45°
60°
sinα
cosα
由上表可知:当为锐角时,正弦值随着角度的增大而 (填“增大”或“减小”);
余弦值随着角度的增大而 (填“增大”或“减小”).
增大
减小
A
B
C
A
B
C
30°
60°
45°
k
2k
k
k
tan 30°=
tan 45°=
tan 60°=
1
同理:
α
30°
45°
60°
sinα
cosα
tanα
1
三角函数
三角函数值
3.特殊角三角函数值表
求下列各式的值:
2sin30°-cos45°
(2) sin60°tan30°
(3) sin230°+ cos230°
sin230°=(sin30°)2
=
-
=
=
=
=
=
1
三.巩固与提高
1.计算:
(1)sin30°+cos30°
(2) sin45°- cos60°+ sin260°
(3)2cos60°+ sin60°+2sin45°cos45°
sin30°+cos30°
2sin60°+ cos45°
(4)
2.下面给出五个式子:
①sin30°+sin60°=2sin45°
②sin60°+cos60°=2(sin30°+cos30°)
③sin60°-sin30°=sin(60°-30°)
④(sin60°+sin30°)(sin60°-sin30°)
=sin260°-sin230°;
⑤sin60°=2sin30°
其中正确的式子的个数是( )
A、1个 B、2个 C、3个 D、4个
A
×
×
×
×
√
3.当锐角A=40°时 ,cosA的值 ( )
A.
B.
C.
D.
B
求满足下列条件的锐角α:
2sinα- =0
(2) tanα- 1=0
α=45°
α=30°
1.填空:
(1) sinA=1,则锐角A= ;
若 sin(β-15°)= ,锐角β= ,
此时cosβ= .
(2)在Rt△ABC中,sinB= ,则cos = .
45°
45°
三.巩固与提高
2.若α为锐角,
(1)若 4cos2α-3=0,求α;
α=30°
(3)△ABC中,若
则∠C= .
60°
四.小结
α
30°
45°
60°
sinα
cosα
tanα
1
三角函数
三角函数值
3.特殊角三角函数值表
课堂检测 47页 1,2
作 业
课本:第48页第1,2,3题
结束寄语
在数学领域中,提出问题的艺术比解答的艺术更为重要.
——康托尔
下课了!
cos A=
1.正弦、余弦、正切、的定义
A
c
b
a
C
B
对边
邻边
斜边
┓
在△ABC中,∠C为直角.
∠A的对边
斜边
a
c
∠A的邻边
斜边
b
c
0<sinA<1
0<cosA<1
sin A=
tanA=
∠A的对边
∠A的邻边
=
a
b
=
=
tan A>0
一.复习巩固:
2.Rt△ABC中,∠C=90°, a:b=5:12,
则△ABC中最小角的正弦值为:
A
B
C
a
=5k
c
=13k
b
=12k
3.判断
(1)锐角β的正弦、余弦的值都不小于1.( )
(2)在△ABC中,∠C=90°,若各边长都扩大10倍,则锐角A的正弦值也扩大10倍. ( )
×
×
4.一直角三角形有两边长为3、4,
则最小角的余弦为:
A
B
C
a
=3
c
=5
b
=4
A
B
C
a
=3
c
=4
=
b
5.若α为锐角,则(填 < > =):
(1)sinα+cosα 1
(2)sin2α+cos2α 1
A
B
C
a
c
b
α
探索与发现
1.请同学们拿出含有30°及含有45°的两块三角板,进行观察与推算sin30°,sin45°,sin60°, cos30°,cos45° ,cos60°的值.
45°
30°
C
C
B
B
A
A
1
1
2
1
60°
二.新课讲解:
探索与发现
45°
30°
C
C
B
B
A
A
k
k
2k
k
60°
二.新课讲解:
1.请同学们拿出含有30°及含有45°的两块三角板,进行观察与推算sin30°,sin45°,sin60°, cos30°,cos45° ,cos60°的值.
2.填表:
α
30°
45°
60°
sinα
cosα
由上表可知:当为锐角时,正弦值随着角度的增大而 (填“增大”或“减小”);
余弦值随着角度的增大而 (填“增大”或“减小”).
增大
减小
A
B
C
A
B
C
30°
60°
45°
k
2k
k
k
tan 30°=
tan 45°=
tan 60°=
1
同理:
α
30°
45°
60°
sinα
cosα
tanα
1
三角函数
三角函数值
3.特殊角三角函数值表
求下列各式的值:
2sin30°-cos45°
(2) sin60°tan30°
(3) sin230°+ cos230°
sin230°=(sin30°)2
=
-
=
=
=
=
=
1
三.巩固与提高
1.计算:
(1)sin30°+cos30°
(2) sin45°- cos60°+ sin260°
(3)2cos60°+ sin60°+2sin45°cos45°
sin30°+cos30°
2sin60°+ cos45°
(4)
2.下面给出五个式子:
①sin30°+sin60°=2sin45°
②sin60°+cos60°=2(sin30°+cos30°)
③sin60°-sin30°=sin(60°-30°)
④(sin60°+sin30°)(sin60°-sin30°)
=sin260°-sin230°;
⑤sin60°=2sin30°
其中正确的式子的个数是( )
A、1个 B、2个 C、3个 D、4个
A
×
×
×
×
√
3.当锐角A=40°时 ,cosA的值 ( )
A.
B.
C.
D.
B
求满足下列条件的锐角α:
2sinα- =0
(2) tanα- 1=0
α=45°
α=30°
1.填空:
(1) sinA=1,则锐角A= ;
若 sin(β-15°)= ,锐角β= ,
此时cosβ= .
(2)在Rt△ABC中,sinB= ,则cos = .
45°
45°
三.巩固与提高
2.若α为锐角,
(1)若 4cos2α-3=0,求α;
α=30°
(3)△ABC中,若
则∠C= .
60°
四.小结
α
30°
45°
60°
sinα
cosα
tanα
1
三角函数
三角函数值
3.特殊角三角函数值表
课堂检测 47页 1,2
作 业
课本:第48页第1,2,3题
结束寄语
在数学领域中,提出问题的艺术比解答的艺术更为重要.
——康托尔
下课了!
