第23章 第6课时 23.3.2 相似三角形的判定(二)-华东师大版九年级数学上册课件(16张)
文档属性
| 名称 | 第23章 第6课时 23.3.2 相似三角形的判定(二)-华东师大版九年级数学上册课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1008.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 00:00:00 | ||
图片预览






文档简介
第23章第6课时
23.3.2 相似三角形的判定(二)
一、课前导学【课前热身】
已知:如图,△ABC 的高AD、BE交于点F.
求证:
.
解:∵????????⊥????????,??????????⊥????????
∴∠????????????=∠????????????=????????。
∵在△????????????和 △AFE中
∠????????????=∠AFE
∴ △????????????? △AFE
∴????????????????=????????????????
?
一、课前导学【自主学习】
阅读教材第67-69页,并完成下列各题
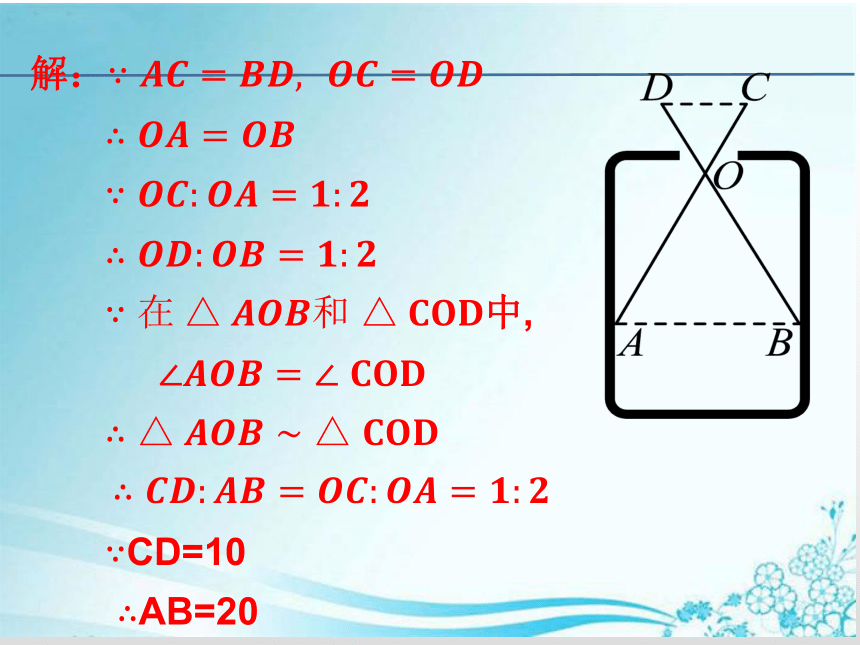
如图,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量内孔直径AB.已知OC∶OA=1∶2,如果量得CD=10,那么AB=2×10=20.你知道这是为什么吗?
解:∵????????=????????,??????????=????????
∴????????=?????????
∵????????:????????=????:????
∴????????:????????=????:????
∵在△????????????和 △????????????中,
∠????????????=∠ ????????????
∴ △????????????? △ ????????????
????????∴????????:????????=????????:????????=????:????
∵CD=10
?????????∴AB=20
?
二、探究与合作
探究点:相似三角形的判定定理2:
1.如图,如果有一点E在边AC上移动,那么点E在什么位置时能使△ADE与△ABC相似呢?
如图所示
二、探究与合作
探究点:相似三角形的判定定理2:
2.图中△ADE与△ABC的一组对应边AD与AB的长度的比值为 ???????? ,将点E由点A开始在AC上移动,可以发现当AE= ???????? AC时,△ADE与△ABC似乎相似,此时???????????????? = 。
?
????????
?
二、探究与合作
3. 猜想:
如果 ,那么这两个三角形相似。
4.已知:如图,在△ABC和△????′????′????′中,∠A=∠A1,
????????????′????′=????????????′????′;
求证:△ABC∽△????′????′????′ ;
?
两个三角形两边成比例且夹角相等
解:在△????????????的边????????上截取????????=????′????′,????????上截取????????=????′????′,连接????????
∵在△????????????和△?????′????′????′中
∠????=∠????′????????=????′????′????????=????′????′
∴ △????????????? △ ????′????′????′??(????????????)
∵????????????′????′=????????????′????′
∴????????????????=????????????????
∴????????∥????????
∴ △?????????????△ ???????????????????∴ △?????????????△ ????′????′????′
?
二、探究与合作
相似三角形的判定定理2:
.
几何语言:∵在△ABC和△A′B′C′中,
.
∴ .
两边对应成比例且夹角相等的两个三角形相似
????????????′????′=????????????′????′,∠????=∠????′
?
△?????????????△ ????′????′????′
?
二、探究与合作
5.如果△ABC与△A′B′C′的两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
解:不一定,如图
结论:要证两个三角形相似,两边对应成比例后,必须是这两边的夹角相等才能证得相似,不是夹角则不一定相似
????
?
????
?
三、例题导析
1.已知:如图,P为△ABC的中线AD上的一点,且BD2=PD·AD. 求证:△ADC∽△CDP.
解:∵????????为△????????????的中线
?????????∴????????=????????
?????????∵?BD2=PD·AD
?????????∴CD2=PD·AD 即????????????????=????????????????
?????????∵∠????????????=∠ ????????????
?????????∴ △ADC∽△CDP
?
三、例题导析
2.如图所示,△ABD∽△ACE,求证:△ABC∽△ADE.
解:?????∵△????????????∽△????????????
????????∴????????????????=????????????????,∠????????????=∠?????????????
∴????????????????=????????????????,∠????????????=∠?????????????
?????????????∴?△ABC∽△ADE
?
三、例题导析
3.如图,已知BD,CE分别为△ABC的高,试说明
△ADE与△ABC相似.
解:∵????????⊥????????,??????????⊥????????
∴∠????????????=∠????????????=????????。
∵在△????????????和 △ ????????????中
∠????=∠A
∴ △????????????? △ ???????????? ????????∴????????????????=????????????????
???????????
?
∴????????????????=?????????????????
∵∠????=∠A
∴ △????????????? △ ????????????
?
及时反馈
1. 如图,在△ABC中,AB=8cm,BC=16 cm,点P从点A开始沿AB边向B点以2 cm/s的速度移动,点Q从点B开始沿BC边向点C以4 cm/s的速度移动,如果P、Q分别从A、B同时出发,多少秒后△PBQ与△ABC相似?
解:设t秒后△PBQ与△ABC相似,则PB=(8-2t)cm,BQ=4t cm
△ABC∽△PBQ时
????????????????=????????????????
∴ ?????????????????=????????????????????????????∴????=????
2.△ABC∽△QBP时
????????????????=????????????????
????????????????????????????????∴ ????????????=????????????????????????????????∴????=????
?
及时反馈
2.某老师讲完“相似三角形的判定”后,出了如下一道思考题:如图,梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,试问:△AOB和△DOC相似吗?
某学生对上题作如下解答:
解:△AOB∽△DOC. 理由如下:
∵AD∥BC,
∴????????????????= ????????????????
又∵∠AOB=∠DOC,
∴△AOB∽△DOC.
请你回答,该学生的解答是否正确?
如果正确,请在每一步后面写出根据;
如果不正确,请简要说明理由.
?
不正确, ????????????????= ????????????????不是△AOB和△DOC的对应边
?
若△AOB∽△DOC
则????????????????= ????????????????
而不是????????????????= ????????????????
23.3.2 相似三角形的判定(二)
一、课前导学【课前热身】
已知:如图,△ABC 的高AD、BE交于点F.
求证:
.
解:∵????????⊥????????,??????????⊥????????
∴∠????????????=∠????????????=????????。
∵在△????????????和 △AFE中
∠????????????=∠AFE
∴ △????????????? △AFE
∴????????????????=????????????????
?
一、课前导学【自主学习】
阅读教材第67-69页,并完成下列各题
如图,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量内孔直径AB.已知OC∶OA=1∶2,如果量得CD=10,那么AB=2×10=20.你知道这是为什么吗?
解:∵????????=????????,??????????=????????
∴????????=?????????
∵????????:????????=????:????
∴????????:????????=????:????
∵在△????????????和 △????????????中,
∠????????????=∠ ????????????
∴ △????????????? △ ????????????
????????∴????????:????????=????????:????????=????:????
∵CD=10
?????????∴AB=20
?
二、探究与合作
探究点:相似三角形的判定定理2:
1.如图,如果有一点E在边AC上移动,那么点E在什么位置时能使△ADE与△ABC相似呢?
如图所示
二、探究与合作
探究点:相似三角形的判定定理2:
2.图中△ADE与△ABC的一组对应边AD与AB的长度的比值为 ???????? ,将点E由点A开始在AC上移动,可以发现当AE= ???????? AC时,△ADE与△ABC似乎相似,此时???????????????? = 。
?
????????
?
二、探究与合作
3. 猜想:
如果 ,那么这两个三角形相似。
4.已知:如图,在△ABC和△????′????′????′中,∠A=∠A1,
????????????′????′=????????????′????′;
求证:△ABC∽△????′????′????′ ;
?
两个三角形两边成比例且夹角相等
解:在△????????????的边????????上截取????????=????′????′,????????上截取????????=????′????′,连接????????
∵在△????????????和△?????′????′????′中
∠????=∠????′????????=????′????′????????=????′????′
∴ △????????????? △ ????′????′????′??(????????????)
∵????????????′????′=????????????′????′
∴????????????????=????????????????
∴????????∥????????
∴ △?????????????△ ???????????????????∴ △?????????????△ ????′????′????′
?
二、探究与合作
相似三角形的判定定理2:
.
几何语言:∵在△ABC和△A′B′C′中,
.
∴ .
两边对应成比例且夹角相等的两个三角形相似
????????????′????′=????????????′????′,∠????=∠????′
?
△?????????????△ ????′????′????′
?
二、探究与合作
5.如果△ABC与△A′B′C′的两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
解:不一定,如图
结论:要证两个三角形相似,两边对应成比例后,必须是这两边的夹角相等才能证得相似,不是夹角则不一定相似
????
?
????
?
三、例题导析
1.已知:如图,P为△ABC的中线AD上的一点,且BD2=PD·AD. 求证:△ADC∽△CDP.
解:∵????????为△????????????的中线
?????????∴????????=????????
?????????∵?BD2=PD·AD
?????????∴CD2=PD·AD 即????????????????=????????????????
?????????∵∠????????????=∠ ????????????
?????????∴ △ADC∽△CDP
?
三、例题导析
2.如图所示,△ABD∽△ACE,求证:△ABC∽△ADE.
解:?????∵△????????????∽△????????????
????????∴????????????????=????????????????,∠????????????=∠?????????????
∴????????????????=????????????????,∠????????????=∠?????????????
?????????????∴?△ABC∽△ADE
?
三、例题导析
3.如图,已知BD,CE分别为△ABC的高,试说明
△ADE与△ABC相似.
解:∵????????⊥????????,??????????⊥????????
∴∠????????????=∠????????????=????????。
∵在△????????????和 △ ????????????中
∠????=∠A
∴ △????????????? △ ???????????? ????????∴????????????????=????????????????
???????????
?
∴????????????????=?????????????????
∵∠????=∠A
∴ △????????????? △ ????????????
?
及时反馈
1. 如图,在△ABC中,AB=8cm,BC=16 cm,点P从点A开始沿AB边向B点以2 cm/s的速度移动,点Q从点B开始沿BC边向点C以4 cm/s的速度移动,如果P、Q分别从A、B同时出发,多少秒后△PBQ与△ABC相似?
解:设t秒后△PBQ与△ABC相似,则PB=(8-2t)cm,BQ=4t cm
△ABC∽△PBQ时
????????????????=????????????????
∴ ?????????????????=????????????????????????????∴????=????
2.△ABC∽△QBP时
????????????????=????????????????
????????????????????????????????∴ ????????????=????????????????????????????????∴????=????
?
及时反馈
2.某老师讲完“相似三角形的判定”后,出了如下一道思考题:如图,梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,试问:△AOB和△DOC相似吗?
某学生对上题作如下解答:
解:△AOB∽△DOC. 理由如下:
∵AD∥BC,
∴????????????????= ????????????????
又∵∠AOB=∠DOC,
∴△AOB∽△DOC.
请你回答,该学生的解答是否正确?
如果正确,请在每一步后面写出根据;
如果不正确,请简要说明理由.
?
不正确, ????????????????= ????????????????不是△AOB和△DOC的对应边
?
若△AOB∽△DOC
则????????????????= ????????????????
而不是????????????????= ????????????????
