第24章 第2课时 24.2直角三角形的性质-华东师大版九年级数学上册课件(16张)
文档属性
| 名称 | 第24章 第2课时 24.2直角三角形的性质-华东师大版九年级数学上册课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 549.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 17:22:59 | ||
图片预览





文档简介
第24章 第2课时
24.2直角三角形的性质
一、课前导学
热身训练:
1.在平行四边形ABCD中,如果∠A=90°,那么四边形ABCD是_________.
2.在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AC=10,则AB=_________.
矩形
一、课前导学
自主预习
阅读教材第102—104页,并完成下列各题
1.直角三角形的两个锐角 ,
2.直角三角形两直角边的平方和等于
(勾股定理).
3.直角三角形斜边上的 等于 的一半.
4.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 。
互余
斜边的平方
中线
斜边
一半
一、课前导学
自主预习
阅读教材第102页至第104页,并完成下列各题.
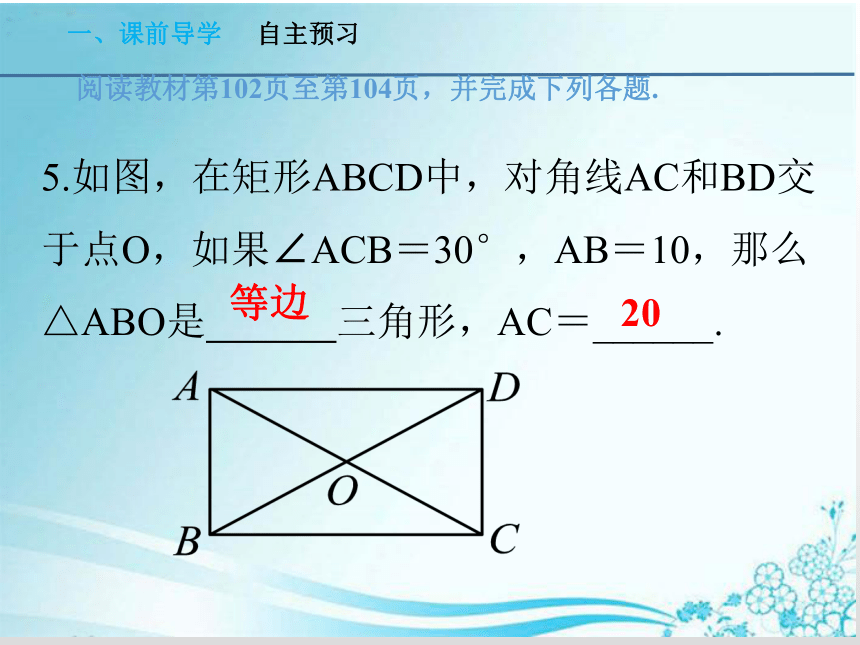
5.如图,在矩形ABCD中,对角线AC和BD交于点O,如果∠ACB=30°,AB=10,那么△ABO是 三角形,AC=______.
等边
20
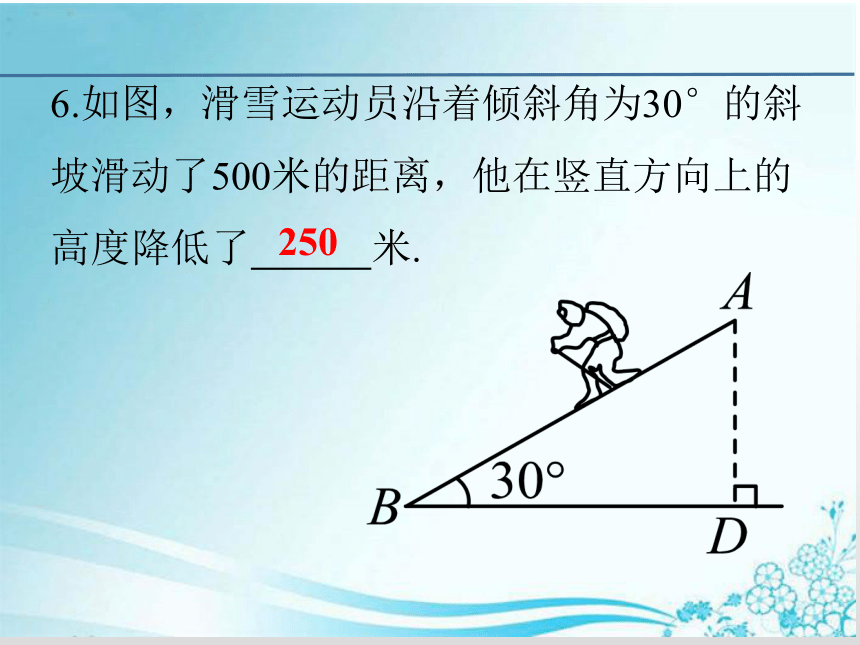
6.如图,滑雪运动员沿着倾斜角为30°的斜坡滑动了500米的距离,他在竖直方向上的高度降低了 米.
250
二、探究与合作
探究点1:直角三角形斜边的中线与斜边的数量关系
如图中②是图①中矩形ABCD的一部分,你知道OB与AC的长度之间的关系吗?
(1)△ABC是 三角形;OB是△ABC的 线.
(2)量一量OB和AC的长度,猜想OB与AC的数量关系.
直角
OB = AC
?
A
B
C
∟
D
【证明】
思路引导:
中线辅助线作法:将中线延长一倍.
延长CD到点E,使DE=CD,连结AE、BE.
E
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90?,
∴ 四边形ACBE是矩形,
∴ CE=AB.
知识探索
归纳:
直角三角形斜边上的中线等于斜边的一半.
符号语言
A
C
B
∟
O
∵在Rt?ABC中,
CD是斜边AB的中线,
及时反馈
1如图,在△ABC中,BC=18,BD⊥AC于点D,CE⊥AB于点E,F,G分别为BC,DE的中点,若ED=10,则FG的长为( )
A. B.9 C.10 D.无法确定
二、探究与合作
2.如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=2,求CD的长.
探究点2:直角三角形30°角所对的直角边与斜边的数量关系
如图,在直角三角形ABC中,∠ABC=90°,∠A=60°,OA=OB.
(1)∠C的度数为 ;
(2)△ABO是 三角形;
(3)OB与OC相等吗?
(4)AB与AC有什么数量关系?
等边
60°
OB与OC
直角三角形30°角所对的直角边与斜边的数量关系
归纳:
∵在Rt△ABC中,∠C=30°
几何语言:
及时反馈二
1.如果一个三角形的三个内角的度数之比为1∶2∶3,那么它的最短边与最长边之比为
( )
A.1∶2 B.1∶3 C.2∶3 D.2∶5
2.已知:如图,在Rt△ABC中,∠C=90°,∠A=30°,E是边BC的中点,BF∥AC,EF∥AB,EF=4 cm.
求:(1)∠F的度数;(2)AB的长.
三、当堂检测
1.如图,在A岛周围20海里水域有暗礁,一艘轮船由西向东航行到点O处时,发现A岛在北偏东60°的方向,且与轮船相距30 海里.该船如果不改变航向,有触暗礁的危险吗?
三、当堂检测
2.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连结AM.
(1)求证:EF= AC;
(2)若∠BAC=45°,求线段AM,DM,BC之间的数量关系.
24.2直角三角形的性质
一、课前导学
热身训练:
1.在平行四边形ABCD中,如果∠A=90°,那么四边形ABCD是_________.
2.在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AC=10,则AB=_________.
矩形
一、课前导学
自主预习
阅读教材第102—104页,并完成下列各题
1.直角三角形的两个锐角 ,
2.直角三角形两直角边的平方和等于
(勾股定理).
3.直角三角形斜边上的 等于 的一半.
4.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 。
互余
斜边的平方
中线
斜边
一半
一、课前导学
自主预习
阅读教材第102页至第104页,并完成下列各题.
5.如图,在矩形ABCD中,对角线AC和BD交于点O,如果∠ACB=30°,AB=10,那么△ABO是 三角形,AC=______.
等边
20
6.如图,滑雪运动员沿着倾斜角为30°的斜坡滑动了500米的距离,他在竖直方向上的高度降低了 米.
250
二、探究与合作
探究点1:直角三角形斜边的中线与斜边的数量关系
如图中②是图①中矩形ABCD的一部分,你知道OB与AC的长度之间的关系吗?
(1)△ABC是 三角形;OB是△ABC的 线.
(2)量一量OB和AC的长度,猜想OB与AC的数量关系.
直角
OB = AC
?
A
B
C
∟
D
【证明】
思路引导:
中线辅助线作法:将中线延长一倍.
延长CD到点E,使DE=CD,连结AE、BE.
E
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90?,
∴ 四边形ACBE是矩形,
∴ CE=AB.
知识探索
归纳:
直角三角形斜边上的中线等于斜边的一半.
符号语言
A
C
B
∟
O
∵在Rt?ABC中,
CD是斜边AB的中线,
及时反馈
1如图,在△ABC中,BC=18,BD⊥AC于点D,CE⊥AB于点E,F,G分别为BC,DE的中点,若ED=10,则FG的长为( )
A. B.9 C.10 D.无法确定
二、探究与合作
2.如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=2,求CD的长.
探究点2:直角三角形30°角所对的直角边与斜边的数量关系
如图,在直角三角形ABC中,∠ABC=90°,∠A=60°,OA=OB.
(1)∠C的度数为 ;
(2)△ABO是 三角形;
(3)OB与OC相等吗?
(4)AB与AC有什么数量关系?
等边
60°
OB与OC
直角三角形30°角所对的直角边与斜边的数量关系
归纳:
∵在Rt△ABC中,∠C=30°
几何语言:
及时反馈二
1.如果一个三角形的三个内角的度数之比为1∶2∶3,那么它的最短边与最长边之比为
( )
A.1∶2 B.1∶3 C.2∶3 D.2∶5
2.已知:如图,在Rt△ABC中,∠C=90°,∠A=30°,E是边BC的中点,BF∥AC,EF∥AB,EF=4 cm.
求:(1)∠F的度数;(2)AB的长.
三、当堂检测
1.如图,在A岛周围20海里水域有暗礁,一艘轮船由西向东航行到点O处时,发现A岛在北偏东60°的方向,且与轮船相距30 海里.该船如果不改变航向,有触暗礁的危险吗?
三、当堂检测
2.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连结AM.
(1)求证:EF= AC;
(2)若∠BAC=45°,求线段AM,DM,BC之间的数量关系.
