第24章 第3课时 24.3.1锐角三角函数的定义及关系的应用-华东师大版九年级数学上册课件(18张)
文档属性
| 名称 | 第24章 第3课时 24.3.1锐角三角函数的定义及关系的应用-华东师大版九年级数学上册课件(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 770.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 17:22:30 | ||
图片预览



文档简介
第24章第3课时
24.3.1锐角三角函数的定义及关系的应用
一、课前导学【课前热身】
1.直角三角形的两锐角 .
2.直角三角形斜边上的中线等于斜边的 .
3.如果直角三角形的两直角边分别为a,b,斜边为c,则有 .
.
????????+????????=????????
?
之和等于????????°
?
一半
?
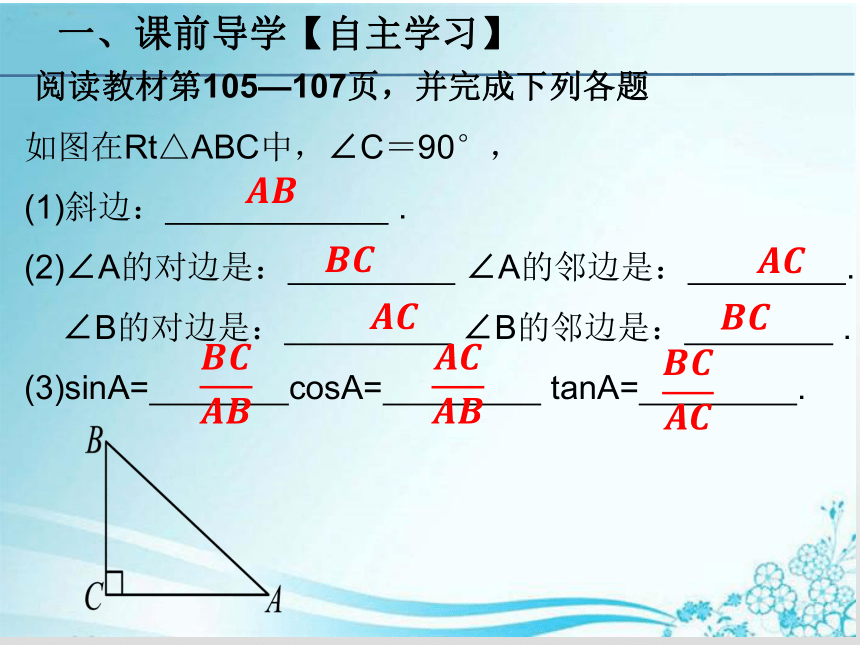
一、课前导学【自主学习】
如图在Rt△ABC中,∠C=90°,
(1)斜边: .
(2)∠A的对边是: ∠A的邻边是: .
∠B的对边是: ∠B的邻边是: .
(3)sinA= cosA= tanA= .
阅读教材第105—107页,并完成下列各题
????????
?
????????
?
????????
?
????????
?
????????
?
????????????????
?
????????????????
?
????????????????
?
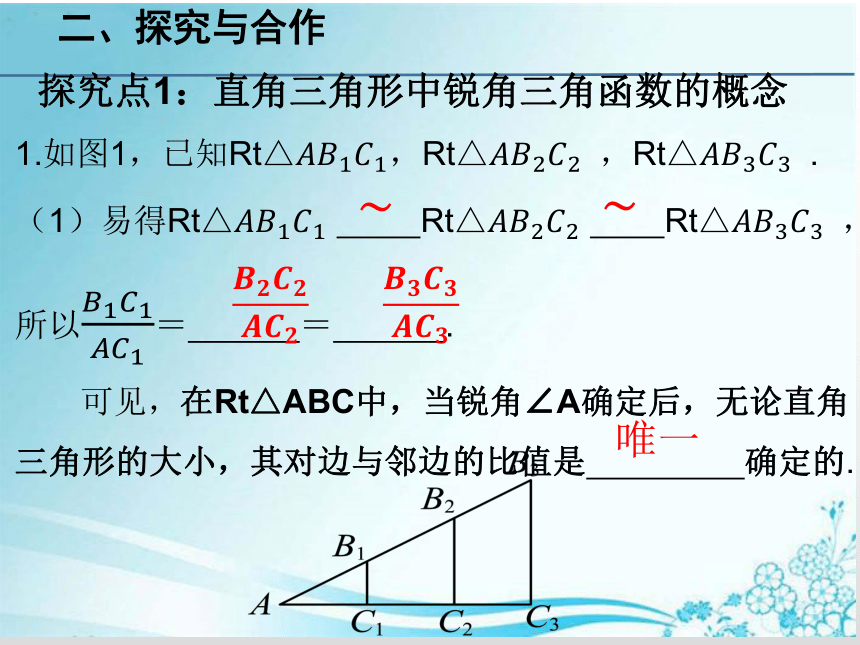
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
1.如图1,已知Rt△????????1????1,Rt△ ????????2????2?,Rt△ ????????3????3?.
(1)易得Rt△ ????????1????1 Rt△ ????????2????2 Rt△ ????????3????3?,所以????1????1????????1= = .
可见,在Rt△ABC中,当锐角∠A确定后,无论直角三角形的大小,其对边与邻边的比值是 确定的.
?
~
?
~
?
????????????????????????????
?
????????????????????????????
?
唯一
?
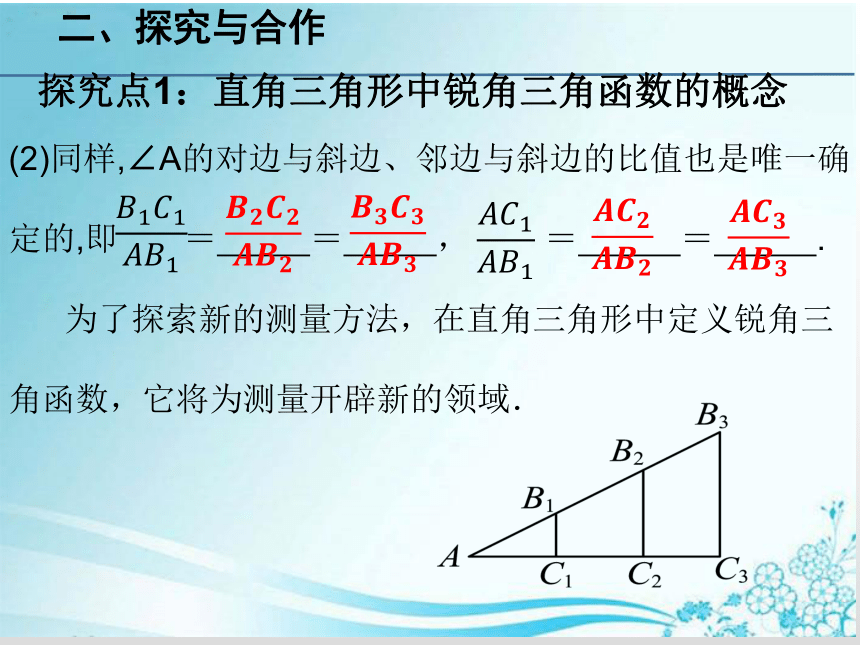
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
(2)同样,∠A的对边与斜边、邻边与斜边的比值也是唯一确定的,即 = = , = = .
为了探索新的测量方法,在直角三角形中定义锐角三角函数,它将为测量开辟新的领域.
????????????????????????????
?
????1????1????????1?
?
????????????????????????????
?
????????1????????1?
?
?????????????????????????
?
?????????????????????????
?
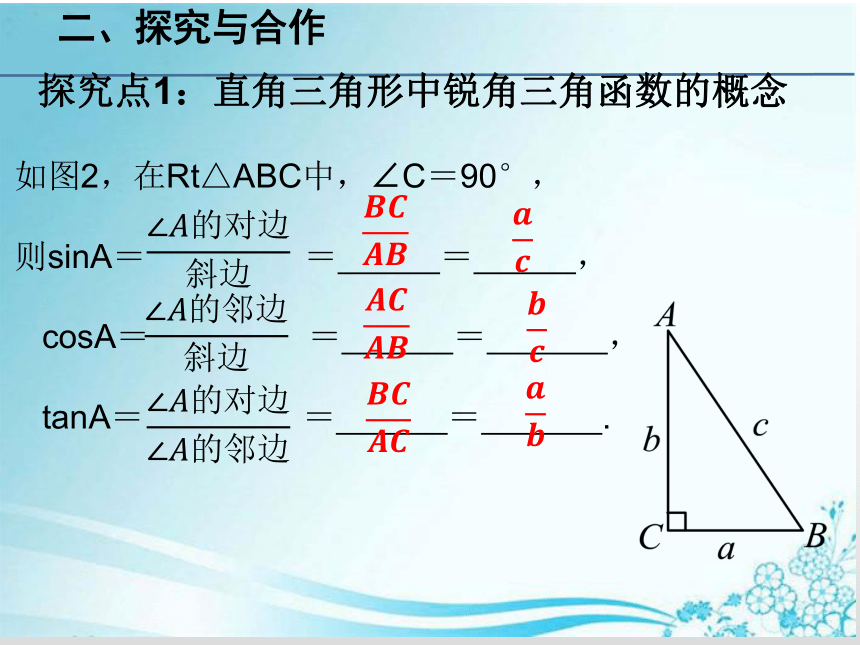
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
如图2,在Rt△ABC中,∠C=90°,
则sinA= = = ,
cosA= = = ,
tanA= = = .
∠????的对边斜边?
?
?????????????????
?
?????????????????
?
?????????????????
?
?????????
?
?????????
?
?????????
?
∠????的邻边斜边?
?
∠????的对边∠????的邻边?
?
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
2.注意:
(1) 弄清“对边” “邻边” “斜边”的含义,在Rt△ABC中,∠C=90°,对∠A来说, 是对边、 是邻边;而对∠B来说,__ __是邻边、__ __是对边,无论怎样,“边”一定要分清.
为了记忆方便,可以用口诀进行记忆,即“正弦等
于 ,余弦等于__ __,正切等于_ _ ”.
????????
?
????????
?
????????
?
????????
?
对比斜
?
邻比斜
?
对比邻
?
二、探究与合作
(3)从定义可以看出,锐角三角函数的三个比值是随着 的变化而变化的,当角度固定不变时,无论边怎样变,它的三个三角函数值是__ __的.
(4)三角函数的符号是一个整体数学符号,如sinA不能看成是sin和A相乘的关系,而是“∠A的正弦”,它的整体表示__ 的比.
(5)会求锐角三角函数的值,在直角三角形中,知道两边,利用勾股定理求 ,再用三角函数的定义求出 .
角度
?
唯一确定
?
对边与斜边
?
第三边
?
锐角三角函数的值
?
二、探究与合作
3.(1)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么sinA= ,cosA= ,tanB= .
(2)在Rt△ABC中,∠C=90°,若cosA= ,则tanB= .
(3)在Rt△ABC中,∠C=90°,若sinA= ,则cosB的值是 .
?????????
?
?????????
?
?????????
?
?????????
?
?????????
?
及时反馈一
1.如图所示,△ABC的顶点是正方形网格的格点,则sinC的值为( )
A. B. C. D.
?????
?
12?
?
55?
?
1010?
?
255?
?
及时反馈一
2.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE= ,求tan∠EBC的值.
13?
?
(1)证明:∵因为四边形ABCD为矩形
∴∠BFE=∠C=90°
?
∵ △BCE沿BE折叠为△BFE
∴∠AFB+∠DFB =180°?∠BFE=90°
?
∵∠AFB+∠ABF =90°
?
∴∠DFE =∠ABF
∴△ABF∽△ DFE
∴∠A=∠D=∠C=90°
?
(2) 在Rt△ABC中, sin∠DFE= ????????????????=????????
?
∴tan∠EBC= tan∠EBF=22
?
∴???????????????? = ?????????????????=22????4?????=2
?
设DE=????,则????????=3????,????????=22????,
????????=????????=3????, ????????=????????=4????
?
?
?
∵△ABF∽△ DFE
二、探究与合作
探究点2:三角函数的取值范围及相关关系
1.在Rt△ABC中,∠C=90°已知锐角a,判断下列结论是否正确。
(1)sin a的值比0大,但比1小;
(2)tan a的值是正值;
(3)0<cos a<1;
(4)?????????????2a+ ????????????2 a=1.
?
√
?
√
?
√
?
√
?
二、探究与合作
探究点2:三角函数的取值范围及相关关系
【归纳总结】
(1)sin a的取值范围为 ;
cos a的取值范围为 ;
tan a的取值范围为 ;
(2)sin a+cos a= ;
(3) = .
0<cos a<1
0<sin a<1
tan a??>0
?
tan a
sin?acos?a?
?
?????
?
二、探究与合作
2.已知sinA·cosA= ,求 ?????????????????????????????????的值.
3.若cosA= ,则3?????????????????????????????????4????????????????+2?????????????????=( )
A. B. C. D.0
?
18?
?
解:?????????????????????????????????????=????????????????????+???????????????????????????????????????????·????????????????
=1—2×????????
=?????????
∴ ?????????????????????????????????=?????????????????????????????????????=????????=????????
?
13?
?
?????
?
47?
?
15?
?
12?
?
及时反馈二
1.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)用签字笔画AD∥BC(D为格点),连结CD;
(2)线段CD的长为________;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是_____,则它所对应的正弦函数值是__ __;
(4)若E为BC中点,则tan∠CAE的值是________.
及时反馈二
2.已知a、b、c分别为△ABC中∠A、∠B、∠C
的对边,若关于x的方程(b+c)????2-2ax+c-b=0有两个相等的实数根,且sinB·cosA-cosB·sinA=0,则△ABC的形状为( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
3.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,△ABC中最小的角为∠A,那么tanA的值为________.
?
?????
?
????????或????????
24.3.1锐角三角函数的定义及关系的应用
一、课前导学【课前热身】
1.直角三角形的两锐角 .
2.直角三角形斜边上的中线等于斜边的 .
3.如果直角三角形的两直角边分别为a,b,斜边为c,则有 .
.
????????+????????=????????
?
之和等于????????°
?
一半
?
一、课前导学【自主学习】
如图在Rt△ABC中,∠C=90°,
(1)斜边: .
(2)∠A的对边是: ∠A的邻边是: .
∠B的对边是: ∠B的邻边是: .
(3)sinA= cosA= tanA= .
阅读教材第105—107页,并完成下列各题
????????
?
????????
?
????????
?
????????
?
????????
?
????????????????
?
????????????????
?
????????????????
?
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
1.如图1,已知Rt△????????1????1,Rt△ ????????2????2?,Rt△ ????????3????3?.
(1)易得Rt△ ????????1????1 Rt△ ????????2????2 Rt△ ????????3????3?,所以????1????1????????1= = .
可见,在Rt△ABC中,当锐角∠A确定后,无论直角三角形的大小,其对边与邻边的比值是 确定的.
?
~
?
~
?
????????????????????????????
?
????????????????????????????
?
唯一
?
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
(2)同样,∠A的对边与斜边、邻边与斜边的比值也是唯一确定的,即 = = , = = .
为了探索新的测量方法,在直角三角形中定义锐角三角函数,它将为测量开辟新的领域.
????????????????????????????
?
????1????1????????1?
?
????????????????????????????
?
????????1????????1?
?
?????????????????????????
?
?????????????????????????
?
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
如图2,在Rt△ABC中,∠C=90°,
则sinA= = = ,
cosA= = = ,
tanA= = = .
∠????的对边斜边?
?
?????????????????
?
?????????????????
?
?????????????????
?
?????????
?
?????????
?
?????????
?
∠????的邻边斜边?
?
∠????的对边∠????的邻边?
?
二、探究与合作
探究点1:直角三角形中锐角三角函数的概念
2.注意:
(1) 弄清“对边” “邻边” “斜边”的含义,在Rt△ABC中,∠C=90°,对∠A来说, 是对边、 是邻边;而对∠B来说,__ __是邻边、__ __是对边,无论怎样,“边”一定要分清.
为了记忆方便,可以用口诀进行记忆,即“正弦等
于 ,余弦等于__ __,正切等于_ _ ”.
????????
?
????????
?
????????
?
????????
?
对比斜
?
邻比斜
?
对比邻
?
二、探究与合作
(3)从定义可以看出,锐角三角函数的三个比值是随着 的变化而变化的,当角度固定不变时,无论边怎样变,它的三个三角函数值是__ __的.
(4)三角函数的符号是一个整体数学符号,如sinA不能看成是sin和A相乘的关系,而是“∠A的正弦”,它的整体表示__ 的比.
(5)会求锐角三角函数的值,在直角三角形中,知道两边,利用勾股定理求 ,再用三角函数的定义求出 .
角度
?
唯一确定
?
对边与斜边
?
第三边
?
锐角三角函数的值
?
二、探究与合作
3.(1)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么sinA= ,cosA= ,tanB= .
(2)在Rt△ABC中,∠C=90°,若cosA= ,则tanB= .
(3)在Rt△ABC中,∠C=90°,若sinA= ,则cosB的值是 .
?????????
?
?????????
?
?????????
?
?????????
?
?????????
?
及时反馈一
1.如图所示,△ABC的顶点是正方形网格的格点,则sinC的值为( )
A. B. C. D.
?????
?
12?
?
55?
?
1010?
?
255?
?
及时反馈一
2.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE= ,求tan∠EBC的值.
13?
?
(1)证明:∵因为四边形ABCD为矩形
∴∠BFE=∠C=90°
?
∵ △BCE沿BE折叠为△BFE
∴∠AFB+∠DFB =180°?∠BFE=90°
?
∵∠AFB+∠ABF =90°
?
∴∠DFE =∠ABF
∴△ABF∽△ DFE
∴∠A=∠D=∠C=90°
?
(2) 在Rt△ABC中, sin∠DFE= ????????????????=????????
?
∴tan∠EBC= tan∠EBF=22
?
∴???????????????? = ?????????????????=22????4?????=2
?
设DE=????,则????????=3????,????????=22????,
????????=????????=3????, ????????=????????=4????
?
?
?
∵△ABF∽△ DFE
二、探究与合作
探究点2:三角函数的取值范围及相关关系
1.在Rt△ABC中,∠C=90°已知锐角a,判断下列结论是否正确。
(1)sin a的值比0大,但比1小;
(2)tan a的值是正值;
(3)0<cos a<1;
(4)?????????????2a+ ????????????2 a=1.
?
√
?
√
?
√
?
√
?
二、探究与合作
探究点2:三角函数的取值范围及相关关系
【归纳总结】
(1)sin a的取值范围为 ;
cos a的取值范围为 ;
tan a的取值范围为 ;
(2)sin a+cos a= ;
(3) = .
0<cos a<1
0<sin a<1
tan a??>0
?
tan a
sin?acos?a?
?
?????
?
二、探究与合作
2.已知sinA·cosA= ,求 ?????????????????????????????????的值.
3.若cosA= ,则3?????????????????????????????????4????????????????+2?????????????????=( )
A. B. C. D.0
?
18?
?
解:?????????????????????????????????????=????????????????????+???????????????????????????????????????????·????????????????
=1—2×????????
=?????????
∴ ?????????????????????????????????=?????????????????????????????????????=????????=????????
?
13?
?
?????
?
47?
?
15?
?
12?
?
及时反馈二
1.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)用签字笔画AD∥BC(D为格点),连结CD;
(2)线段CD的长为________;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是_____,则它所对应的正弦函数值是__ __;
(4)若E为BC中点,则tan∠CAE的值是________.
及时反馈二
2.已知a、b、c分别为△ABC中∠A、∠B、∠C
的对边,若关于x的方程(b+c)????2-2ax+c-b=0有两个相等的实数根,且sinB·cosA-cosB·sinA=0,则△ABC的形状为( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
3.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,△ABC中最小的角为∠A,那么tanA的值为________.
?
?????
?
????????或????????
