华东师大版九年级数学上册课件:24.4.2解直角三角形的应用(方向角、俯角、仰角)(20张PPT)
文档属性
| 名称 | 华东师大版九年级数学上册课件:24.4.2解直角三角形的应用(方向角、俯角、仰角)(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 819.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 18:17:10 | ||
图片预览







文档简介
第24章 第6课时
24.4.2 解直角三角形的应用
(方向角、俯角、仰角)
一、课前导学
【热身训练】
1.解直角三角形的主要依据是什么?
2.解直角三角形主要有哪两个类型?
主要依据是:
勾股定理和直角三角形的两个锐角互余
①已知一边和一个角
②已知两条边
【自主学习】阅读教材第113—114页,并完成下列各题
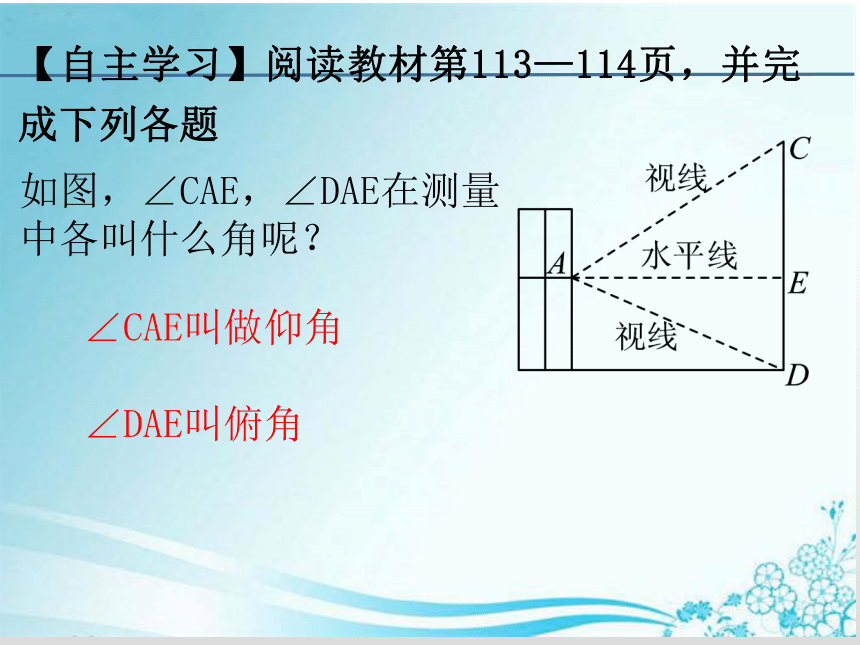
1.肖颖的教室在教学楼的二楼,一天,他站在教室的窗台前看操场上的旗杆,心想:“站在二楼可以利用解直角三角形测得旗杆的高度吗?”他望着旗杆顶端和旗杆底部,可以测得视线与水平线之间的夹角各一个,但是,这两个角怎样命名区别呢?
【自主学习】阅读教材第113—114页,并完成下列各题
如图,∠CAE,∠DAE在测量中各叫什么角呢?
∠CAE叫做仰角
∠DAE叫俯角
2.仰角是指什么角?
(视线在水平线的 ,视线与水平线的夹角)
3.俯角是指什么角?
(视线在水平线的 ,视线与水平线的夹角)
4.方向角是指什么角?
指南或指北的方向线与目标方向线构成的小于 ______ 的角
上方
下方
90°
二、探究与合作
探究点1:与仰角、俯角有关的计算
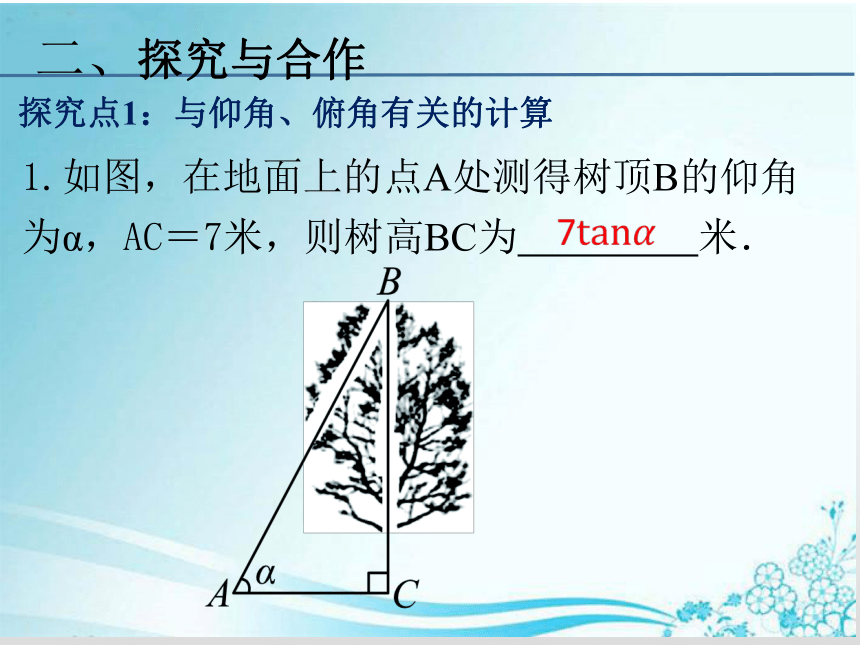
1.如图,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为 米.
7tan????
?
2.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5 m,则大树的高度为 _m(结果保留根号).
53+5
?
及时反馈一
1.如图,为了测量顶部不能到达的建筑物AB的高度,先在地平面上取一点C,用测量仪测得点A的仰角为45°,再向后退20米取一点D,使点D在BC的延长线上,此时测得点A的仰角为30°,已知测量仪的高为1.5米,求建筑物AB的高度.
解:
?????????????????????中,????????=????????tan45°=????????
?
?????????????????????中,????????=????????tan30°=3????????
?
∴????????=?????????????????
?
=3?1????????=20
?
∴AG=103+10
?
∵????????=1.5
?
∴AB=????????+????????=(103+232) 米
?
2. 如图,小强同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小明同学,发现自己的位置与风筝C处和旗杆PQ的顶点P在同一直线上.
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离(结果保留根号);
解:
?????????????????????中,AQ=????????tan45°=10
?
?????????????????????中,BQ=????????tan30°=103
?
∴AB=????????+????????=(103+10) 米
?
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,求A、C两点间的距离(结果保留根号).
E
解:如图,过A作 AE⊥BC于E
?????????????????????中,∠B=30°
?
且AB=103+10
?
∴????????=sin30°×????????=12103+10=53+5
?
∵∠????????????=75°, ∠B=30°
?
∴∠????=45°
?
E
?????????????????????中,AC=????????sin45°=53+522=56+52米
?
探究点2:与方位角有关的计算
1.王英同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时王英同学距离A地( )
A.503 m B.100 m
C.150 m D.1003 m
?
D
2. 如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(3??+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
?
解:如图,过M作 MN⊥AB于N,设MN=x m
N
?????????????????????中,
?
∵∠ANM=90°,∠MAN=30°
?
∴????????=2MN=2????
?
????N=3MN=3????
?
?????????????????????中,
?
∵∠BNM=90°,∠MBN=45°
?
∴BN=MN=????,
?
BM=2MN=2????
?
∵AN+BN=AB
?
∴3????+????=300(√3???+1)
?
∴????=300
?
∴????????=2????=600
?
∴????????=2????=3002
?
及时反馈二
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距 ?????????????????海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)求出A与C 之间的距离AC.
E
解:如图,过C作 CE⊥AB于E,设AE=x m
?????????????????????中,
?
∵∠AEC=90°,∠CAE=60°
?
∴????C=2AE=2????
?
CE=3AE=3????
?
?????????????????????中,
?
∵∠BEC=90°,∠EBC=45°
?
∴B????=CE=3????,
?
∵AE+BE=AB
?
∴3????+????=50(√3???+1)
?
∴????=50
?
∴????????=2????=100
?
∴????与?????之间的距离为100海里
?
(2)已知距观测点D处50海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?
(参考数据: ???≈1.41, ?????≈1.73)
解:如图,过D作 DF⊥AC于F,设AF=x m
F
?????????????????????中,
?
∵∠AFD=90°,∠DAF=60°
?
∴DF=3AF=3x
?
?????????????????????中,
?
∵∠CFD=90°,∠C????????=45°
?
∴DF=CF=3????,
?
∵AF+CF=AC
?
∴3????+????=100
?
∴????=503-50
?
F
∴DF=3????=1503-50 3
?
≈63.2??海里
?
∵63.2>50
?
∴巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险
24.4.2 解直角三角形的应用
(方向角、俯角、仰角)
一、课前导学
【热身训练】
1.解直角三角形的主要依据是什么?
2.解直角三角形主要有哪两个类型?
主要依据是:
勾股定理和直角三角形的两个锐角互余
①已知一边和一个角
②已知两条边
【自主学习】阅读教材第113—114页,并完成下列各题
1.肖颖的教室在教学楼的二楼,一天,他站在教室的窗台前看操场上的旗杆,心想:“站在二楼可以利用解直角三角形测得旗杆的高度吗?”他望着旗杆顶端和旗杆底部,可以测得视线与水平线之间的夹角各一个,但是,这两个角怎样命名区别呢?
【自主学习】阅读教材第113—114页,并完成下列各题
如图,∠CAE,∠DAE在测量中各叫什么角呢?
∠CAE叫做仰角
∠DAE叫俯角
2.仰角是指什么角?
(视线在水平线的 ,视线与水平线的夹角)
3.俯角是指什么角?
(视线在水平线的 ,视线与水平线的夹角)
4.方向角是指什么角?
指南或指北的方向线与目标方向线构成的小于 ______ 的角
上方
下方
90°
二、探究与合作
探究点1:与仰角、俯角有关的计算
1.如图,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为 米.
7tan????
?
2.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5 m,则大树的高度为 _m(结果保留根号).
53+5
?
及时反馈一
1.如图,为了测量顶部不能到达的建筑物AB的高度,先在地平面上取一点C,用测量仪测得点A的仰角为45°,再向后退20米取一点D,使点D在BC的延长线上,此时测得点A的仰角为30°,已知测量仪的高为1.5米,求建筑物AB的高度.
解:
?????????????????????中,????????=????????tan45°=????????
?
?????????????????????中,????????=????????tan30°=3????????
?
∴????????=?????????????????
?
=3?1????????=20
?
∴AG=103+10
?
∵????????=1.5
?
∴AB=????????+????????=(103+232) 米
?
2. 如图,小强同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小明同学,发现自己的位置与风筝C处和旗杆PQ的顶点P在同一直线上.
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离(结果保留根号);
解:
?????????????????????中,AQ=????????tan45°=10
?
?????????????????????中,BQ=????????tan30°=103
?
∴AB=????????+????????=(103+10) 米
?
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,求A、C两点间的距离(结果保留根号).
E
解:如图,过A作 AE⊥BC于E
?????????????????????中,∠B=30°
?
且AB=103+10
?
∴????????=sin30°×????????=12103+10=53+5
?
∵∠????????????=75°, ∠B=30°
?
∴∠????=45°
?
E
?????????????????????中,AC=????????sin45°=53+522=56+52米
?
探究点2:与方位角有关的计算
1.王英同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时王英同学距离A地( )
A.503 m B.100 m
C.150 m D.1003 m
?
D
2. 如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(3??+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
?
解:如图,过M作 MN⊥AB于N,设MN=x m
N
?????????????????????中,
?
∵∠ANM=90°,∠MAN=30°
?
∴????????=2MN=2????
?
????N=3MN=3????
?
?????????????????????中,
?
∵∠BNM=90°,∠MBN=45°
?
∴BN=MN=????,
?
BM=2MN=2????
?
∵AN+BN=AB
?
∴3????+????=300(√3???+1)
?
∴????=300
?
∴????????=2????=600
?
∴????????=2????=3002
?
及时反馈二
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距 ?????????????????海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)求出A与C 之间的距离AC.
E
解:如图,过C作 CE⊥AB于E,设AE=x m
?????????????????????中,
?
∵∠AEC=90°,∠CAE=60°
?
∴????C=2AE=2????
?
CE=3AE=3????
?
?????????????????????中,
?
∵∠BEC=90°,∠EBC=45°
?
∴B????=CE=3????,
?
∵AE+BE=AB
?
∴3????+????=50(√3???+1)
?
∴????=50
?
∴????????=2????=100
?
∴????与?????之间的距离为100海里
?
(2)已知距观测点D处50海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?
(参考数据: ???≈1.41, ?????≈1.73)
解:如图,过D作 DF⊥AC于F,设AF=x m
F
?????????????????????中,
?
∵∠AFD=90°,∠DAF=60°
?
∴DF=3AF=3x
?
?????????????????????中,
?
∵∠CFD=90°,∠C????????=45°
?
∴DF=CF=3????,
?
∵AF+CF=AC
?
∴3????+????=100
?
∴????=503-50
?
F
∴DF=3????=1503-50 3
?
≈63.2??海里
?
∵63.2>50
?
∴巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险
