沪教版(上海)数学七年级下册-12.7 分数指数幂(2) 课件(24张)
文档属性
| 名称 | 沪教版(上海)数学七年级下册-12.7 分数指数幂(2) 课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 23:30:50 | ||
图片预览






文档简介
§12.7分数指数幂(2)
教学目标
1、理解分数指数幂的意义:能将方根与指数幂互化,体会转化思想。(重点)
2、能在简单的运算中运用有理数指数幂的性质进行计算。(难点)
复习(问1)
1 整数指数幂的运算法则:
2 负整数指数幂的运算法则:
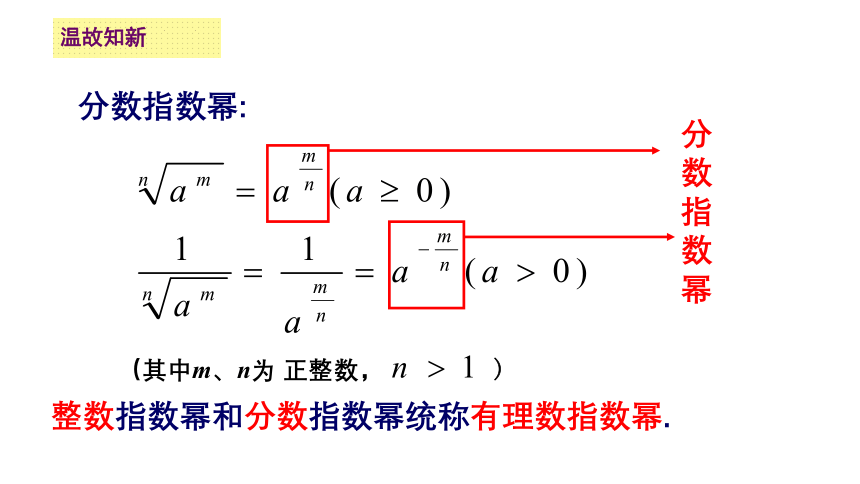
温故知新
分数指数幂:
(其中m、n为 正整数, )
分
数
指
数
幂
整数指数幂和分数指数幂统称有理数指数幂.
整数指数幂和分数指数幂统称有理数指数幂?.
有理数指数幂
有理数指数幂的运算性质:
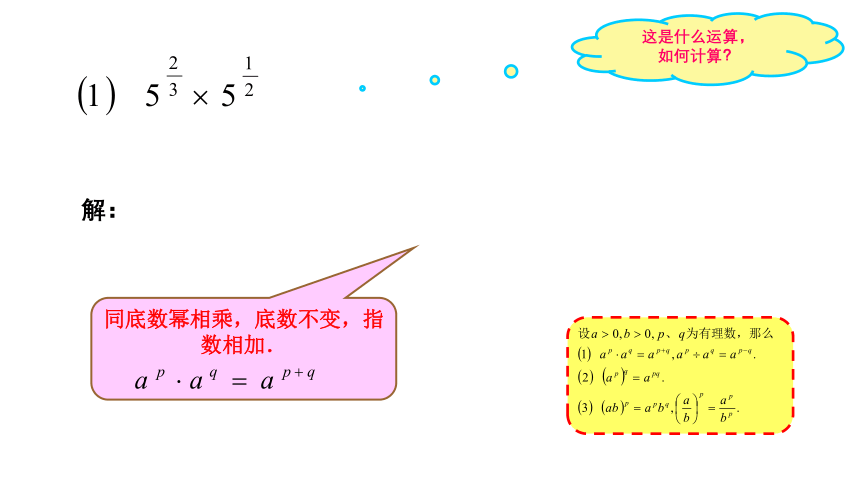
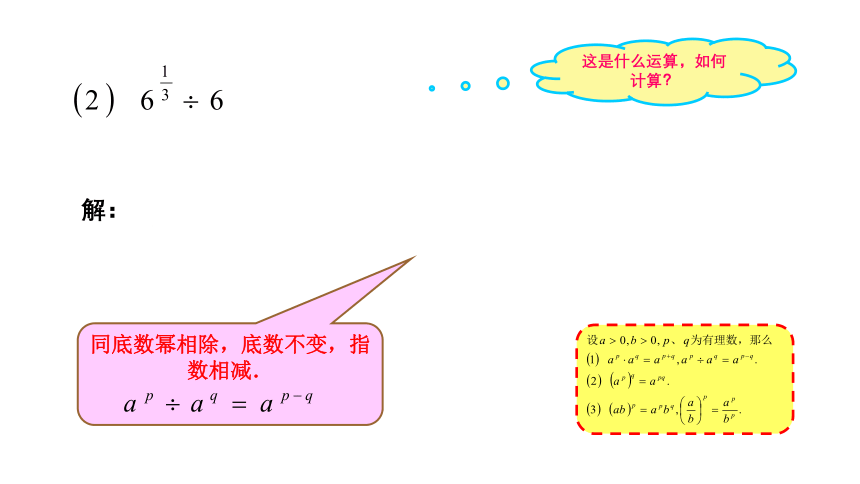
设 , , 、 为有理数,那么
,
(ⅰ) ,
(ⅱ)
(ⅲ) ,
,
例1 计算(结果用幂的形式表示):
(1) ; (2) ;
学习新课
(3) ; (4) .
解:
这是什么运算,
如何计算?
同底数幂相乘,底数不变,指数相加.
解:
这是什么运算,如何计算?
同底数幂相除,底数不变,指数相减.
解:
这是什么运算,如何计算?
幂的乘方,底数不变,指数相乘.
如何计算?
可以先运用积的乘方的逆运算化为 ,再进行计算.
解:
判断是什么运算
运用法则计算
分数指数幂计算的
一般步骤:
小试牛刀:计算(结果用幂的形式表示):
这是什么运算,
法则?
例2 计算:
(1) ;(2) ;
(3) ;(4) .
学习新课
解:
(1)
如何计算?
=
=
=
6
可以先运用积的乘方
进行计算.
解:
(2)
如何计算?
=
=
=
4
可以先运用积的乘方的逆运算 ,化
为 再进行计算.
(3)
如何计算?
解:
=
=
=
=
可以先运用积的乘方
进行计算.
(4)
如何计算?
解:
=
=
=
=
=
=
1
转化为底数相同的形式.
可以先运用积的乘方
进行计算.
通过今天的学习你有什么
收获?
我的感悟我的收获
乘方
幂
开方
根式
正分数指数幂
正整数指数幂
零指数幂与负整数指数幂
负分数指数幂
整数指数幂
分数指数幂
有理数指数幂
小结:
指数加减底不变,同底数幂相乘除.
指数相乘底不变,幂的乘方要清楚.
积商乘方原指数,换底乘方再乘除.
非零数的零次幂,常值为 1不糊涂.
负整数的指数幂,指数转正求倒数.
看到分数指数幂,想到底数必非负.
乘方指数是分子,根指数要当分母.
判断是什么运算
运用法则计算
分数指数幂计算的一般步骤:
在合作中成长
在创新中发展
教学目标
1、理解分数指数幂的意义:能将方根与指数幂互化,体会转化思想。(重点)
2、能在简单的运算中运用有理数指数幂的性质进行计算。(难点)
复习(问1)
1 整数指数幂的运算法则:
2 负整数指数幂的运算法则:
温故知新
分数指数幂:
(其中m、n为 正整数, )
分
数
指
数
幂
整数指数幂和分数指数幂统称有理数指数幂.
整数指数幂和分数指数幂统称有理数指数幂?.
有理数指数幂
有理数指数幂的运算性质:
设 , , 、 为有理数,那么
,
(ⅰ) ,
(ⅱ)
(ⅲ) ,
,
例1 计算(结果用幂的形式表示):
(1) ; (2) ;
学习新课
(3) ; (4) .
解:
这是什么运算,
如何计算?
同底数幂相乘,底数不变,指数相加.
解:
这是什么运算,如何计算?
同底数幂相除,底数不变,指数相减.
解:
这是什么运算,如何计算?
幂的乘方,底数不变,指数相乘.
如何计算?
可以先运用积的乘方的逆运算化为 ,再进行计算.
解:
判断是什么运算
运用法则计算
分数指数幂计算的
一般步骤:
小试牛刀:计算(结果用幂的形式表示):
这是什么运算,
法则?
例2 计算:
(1) ;(2) ;
(3) ;(4) .
学习新课
解:
(1)
如何计算?
=
=
=
6
可以先运用积的乘方
进行计算.
解:
(2)
如何计算?
=
=
=
4
可以先运用积的乘方的逆运算 ,化
为 再进行计算.
(3)
如何计算?
解:
=
=
=
=
可以先运用积的乘方
进行计算.
(4)
如何计算?
解:
=
=
=
=
=
=
1
转化为底数相同的形式.
可以先运用积的乘方
进行计算.
通过今天的学习你有什么
收获?
我的感悟我的收获
乘方
幂
开方
根式
正分数指数幂
正整数指数幂
零指数幂与负整数指数幂
负分数指数幂
整数指数幂
分数指数幂
有理数指数幂
小结:
指数加减底不变,同底数幂相乘除.
指数相乘底不变,幂的乘方要清楚.
积商乘方原指数,换底乘方再乘除.
非零数的零次幂,常值为 1不糊涂.
负整数的指数幂,指数转正求倒数.
看到分数指数幂,想到底数必非负.
乘方指数是分子,根指数要当分母.
判断是什么运算
运用法则计算
分数指数幂计算的一般步骤:
在合作中成长
在创新中发展
