华东师大版 七年级数学下10.1.2 轴对称的再认识教学课件 (22张PPT)
文档属性
| 名称 | 华东师大版 七年级数学下10.1.2 轴对称的再认识教学课件 (22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览





文档简介
10.1.2轴对称的再认识
华师大版七年级数学下册
学习目标
1.能识别常见几何图形中的轴对称图形;
2.画出轴对称图形的对称轴。
3.运用轴对称的特征性质解题
如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形。
这条直线叫这个图形的对称轴。
一、回顾旧知
1、什么是轴对称图形?
A
B
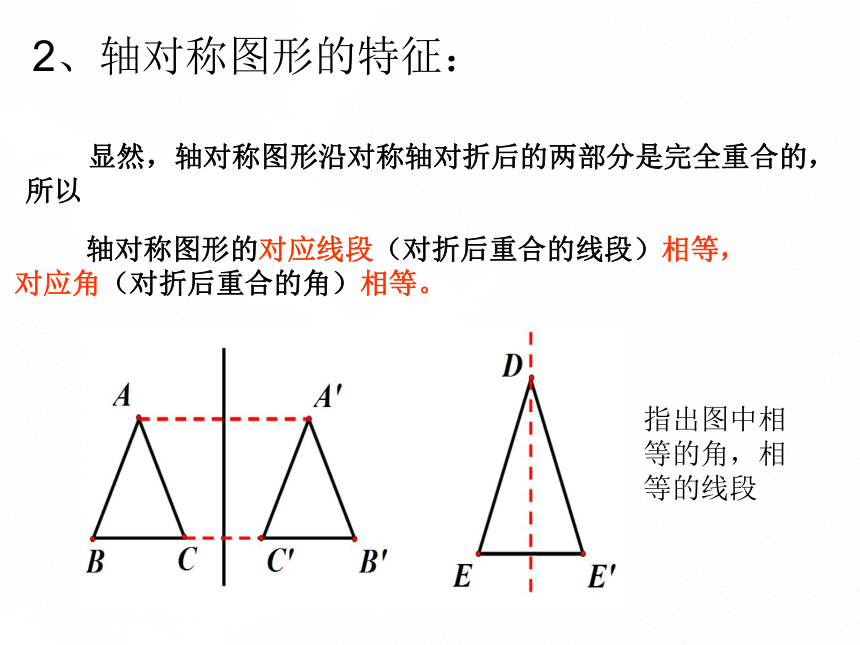
显然,轴对称图形沿对称轴对折后的两部分是完全重合的,所以
轴对称图形的对应线段(对折后重合的线段)相等,
对应角(对折后重合的角)相等。
2、轴对称图形的特征:
指出图中相等的角,相等的线段
做一做:在半透明纸上画出线段AB和它的中点O,再过O点画与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合?
二、新知探究:
1、线段是轴对称图形吗?
结论:线段是轴对称图形
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,简称为中垂线.
注: 线段的垂直平分线是一条直线.
垂直平分线的定义:
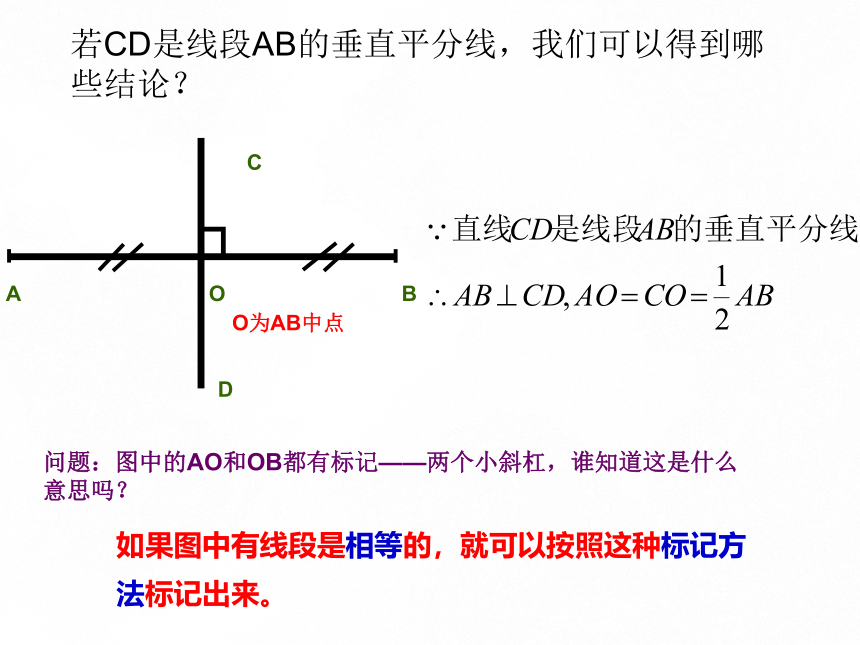
问题:图中的AO和OB都有标记——两个小斜杠,谁知道这是什么意思吗?
如果图中有线段是相等的,就可以按照这种标记方法标记出来。
C
B
A
O
D
O为AB中点
若CD是线段AB的垂直平分线,我们可以得到哪些结论?
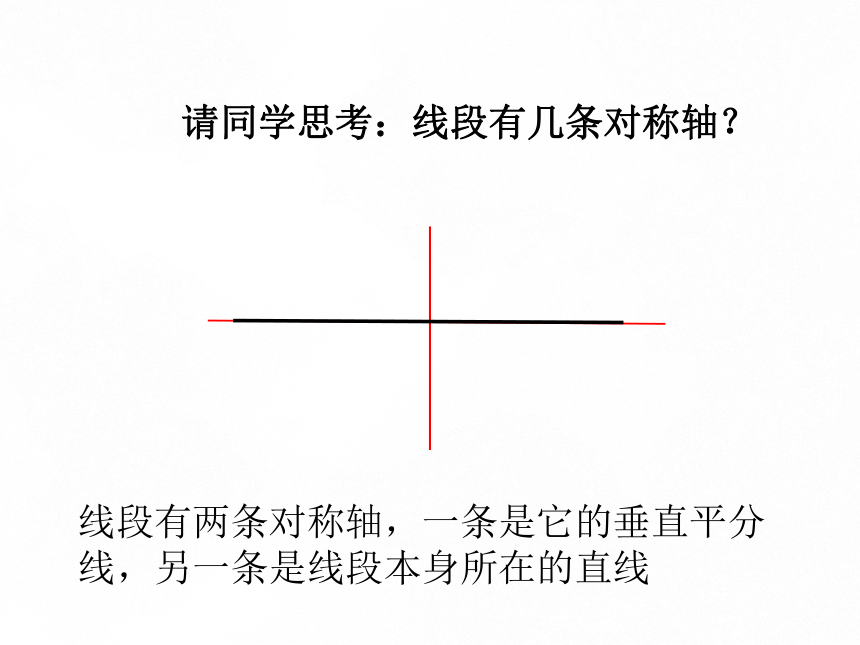
请同学思考:线段有几条对称轴?
线段有两条对称轴,一条是它的垂直平分线,另一条是线段本身所在的直线
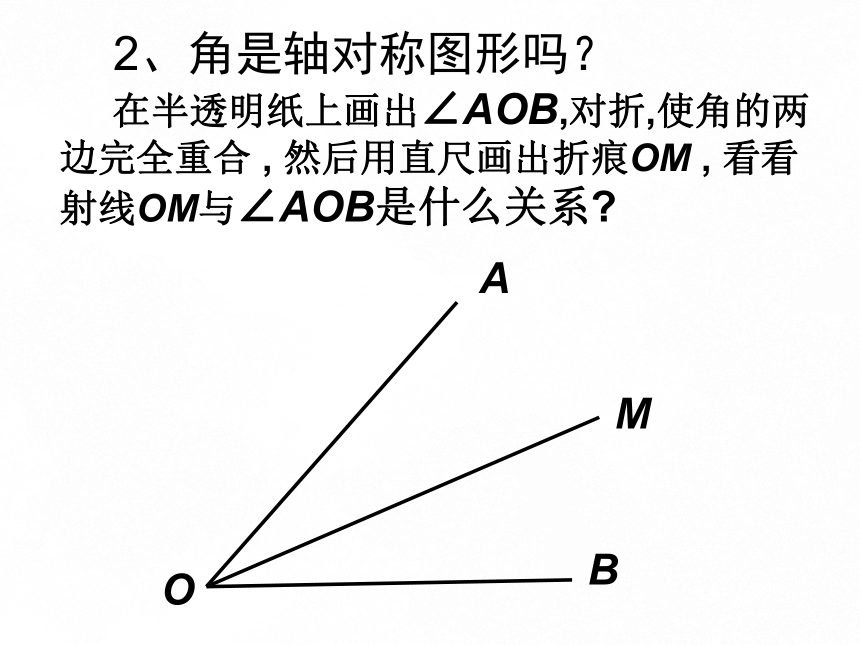
在半透明纸上画出∠AOB,对折,使角的两边完全重合 , 然后用直尺画出折痕OM , 看看射线OM与∠AOB是什么关系?
A
O
B
M
2、角是轴对称图形吗?
结论
(1)角是轴对称图形
A
O
B
M
(2)对称轴是它的角平分线所在的直线
3、当我们看到一个图形,感觉它是轴对称的,该如何来验证呢?
这就需要我们去找到它的对称轴,看看沿着对称轴翻折以后两部分是否重合.
(1)试一试:如图,方格子内的两图形都是成轴对称的,请用红色的笔画出它们的对称轴.
在上图中,由于图形在方格子内,我们可以凭直觉很准确地画出两个图形的对称轴,你能想想是什么原因吗?
因为在方格子中我们比较容易看清楚图形的位置,也就比较容易确定图形的中间位置.
如图,点A和点A’关于某条直线成轴对称,你能画出这条直线吗?
(2)已知对称点画对称轴
A . . A’
能总结你画对称轴的方法吗?
如果没有方格子,而又不能折叠,你还能比较容易地画出图形的对称轴吗?
试试看:如下图的对称轴我们应该如何去画呢?
总结一下刚才画对称轴的方法:
1.找出轴对称图形的任意一组对称点,
3.画出这条线段的垂直平分线.
则这条垂直平分线就是它的对称轴.
2.连结对称点,得到一条线段
1、如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
2、连接对称点的线段被对称轴垂直平分
通过以上的操作,我们有下面的结论:
.
B
A
C
D
E
F
将矩形ABCD沿着对角线AC对折,
则 度数为 。
对边平行即AB∥CD
AC为对称轴
70?
三、典例讲解
四、巩固练习
B
D
B
115?
(画一条即可)
五、畅谈收获
1. 画图形的对称轴的方法:
(1)找出轴对称图形的任意一组对称点。
(2)连结对称点。
(3)画出对称点所连线段的垂直平分线,
就是该图形的对称轴
如果一个图形关于某一条直线对称,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
2.轴对称性质:
如图,爱动脑的小明画对称轴时是按如下步骤完成的,
(1)找出两组对称点,A和A',C和C'
(2)分别连结AA',CC',得到线段AA'和CC'
(3)过这两条线段中点画直线EF,直线EF即为所求
他做得对吗?为什么?
E
F
画对称轴的另一种画法:(1)找出图形中任意两组对称点
(2)连结对称点,得到两条线段
(3)画出过这两条线段中点的直线,就得到了图形的对称轴
六、课后思考
华师大版七年级数学下册
学习目标
1.能识别常见几何图形中的轴对称图形;
2.画出轴对称图形的对称轴。
3.运用轴对称的特征性质解题
如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形。
这条直线叫这个图形的对称轴。
一、回顾旧知
1、什么是轴对称图形?
A
B
显然,轴对称图形沿对称轴对折后的两部分是完全重合的,所以
轴对称图形的对应线段(对折后重合的线段)相等,
对应角(对折后重合的角)相等。
2、轴对称图形的特征:
指出图中相等的角,相等的线段
做一做:在半透明纸上画出线段AB和它的中点O,再过O点画与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合?
二、新知探究:
1、线段是轴对称图形吗?
结论:线段是轴对称图形
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,简称为中垂线.
注: 线段的垂直平分线是一条直线.
垂直平分线的定义:
问题:图中的AO和OB都有标记——两个小斜杠,谁知道这是什么意思吗?
如果图中有线段是相等的,就可以按照这种标记方法标记出来。
C
B
A
O
D
O为AB中点
若CD是线段AB的垂直平分线,我们可以得到哪些结论?
请同学思考:线段有几条对称轴?
线段有两条对称轴,一条是它的垂直平分线,另一条是线段本身所在的直线
在半透明纸上画出∠AOB,对折,使角的两边完全重合 , 然后用直尺画出折痕OM , 看看射线OM与∠AOB是什么关系?
A
O
B
M
2、角是轴对称图形吗?
结论
(1)角是轴对称图形
A
O
B
M
(2)对称轴是它的角平分线所在的直线
3、当我们看到一个图形,感觉它是轴对称的,该如何来验证呢?
这就需要我们去找到它的对称轴,看看沿着对称轴翻折以后两部分是否重合.
(1)试一试:如图,方格子内的两图形都是成轴对称的,请用红色的笔画出它们的对称轴.
在上图中,由于图形在方格子内,我们可以凭直觉很准确地画出两个图形的对称轴,你能想想是什么原因吗?
因为在方格子中我们比较容易看清楚图形的位置,也就比较容易确定图形的中间位置.
如图,点A和点A’关于某条直线成轴对称,你能画出这条直线吗?
(2)已知对称点画对称轴
A . . A’
能总结你画对称轴的方法吗?
如果没有方格子,而又不能折叠,你还能比较容易地画出图形的对称轴吗?
试试看:如下图的对称轴我们应该如何去画呢?
总结一下刚才画对称轴的方法:
1.找出轴对称图形的任意一组对称点,
3.画出这条线段的垂直平分线.
则这条垂直平分线就是它的对称轴.
2.连结对称点,得到一条线段
1、如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
2、连接对称点的线段被对称轴垂直平分
通过以上的操作,我们有下面的结论:
.
B
A
C
D
E
F
将矩形ABCD沿着对角线AC对折,
则 度数为 。
对边平行即AB∥CD
AC为对称轴
70?
三、典例讲解
四、巩固练习
B
D
B
115?
(画一条即可)
五、畅谈收获
1. 画图形的对称轴的方法:
(1)找出轴对称图形的任意一组对称点。
(2)连结对称点。
(3)画出对称点所连线段的垂直平分线,
就是该图形的对称轴
如果一个图形关于某一条直线对称,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
2.轴对称性质:
如图,爱动脑的小明画对称轴时是按如下步骤完成的,
(1)找出两组对称点,A和A',C和C'
(2)分别连结AA',CC',得到线段AA'和CC'
(3)过这两条线段中点画直线EF,直线EF即为所求
他做得对吗?为什么?
E
F
画对称轴的另一种画法:(1)找出图形中任意两组对称点
(2)连结对称点,得到两条线段
(3)画出过这两条线段中点的直线,就得到了图形的对称轴
六、课后思考
