华东师大版 七年级数学下册课件:第八章一元一次不等式复习(共42张PPT)
文档属性
| 名称 | 华东师大版 七年级数学下册课件:第八章一元一次不等式复习(共42张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 23:36:56 | ||
图片预览










文档简介
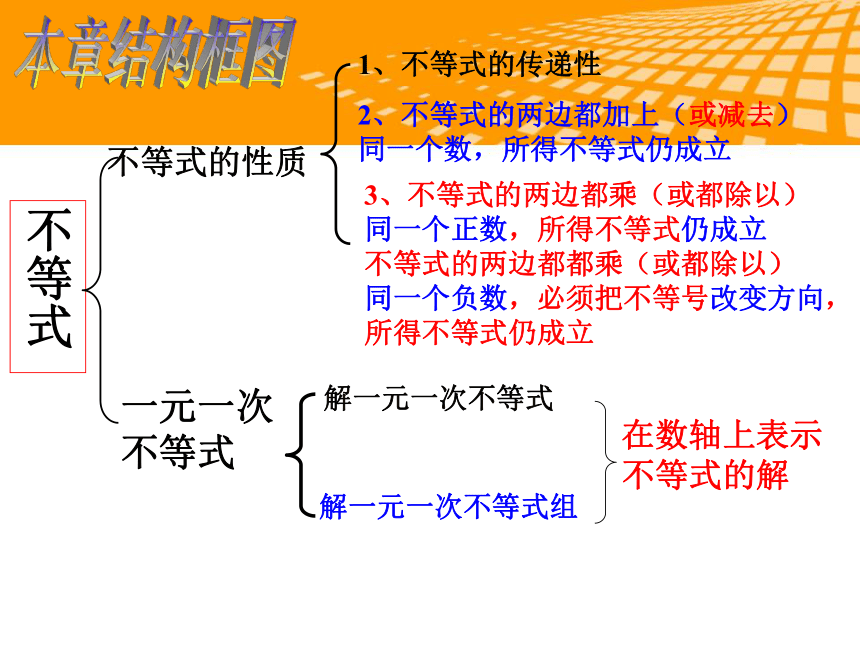
不等式
不等式的性质
1、不等式的传递性
2、不等式的两边都加上(或减去)
同一个数,所得不等式仍成立
3、不等式的两边都乘(或都除以)
同一个正数,所得不等式仍成立
不等式的两边都都乘(或都除以)
同一个负数,必须把不等号改变方向,所得不等式仍成立
一元一次
不等式
解一元一次不等式
解一元一次不等式组
在数轴上表示
不等式的解
*
用不等式表示不相等的数量关系(即列不等式)时,要正确理解其中的关键词语,恰当选用不等号。这种关键词语大致上可以分为以下几种情况,请在空格里填上适当的不等号。
关键
词语
第一类
(明确表明数量的不等关系)
第二类
(明确表明数量的范围特征)
大于、
比..大
小于、
比..小
不大于
不超过
至多
不小于
不低于
至少
正数
负数
非正数
非负数
不等号
0
0
0
0
>
<
≤
≥
>
<
≤
≥
根据下列数量关系列不等式:
⑴、a不是正数。
⑵、x与y的一半的差大于-3。
⑶、y的70%与5的和是非负数。
⑷、3与x的倒数的差小于5。
⑸、a的立方根不等于a。
上述不等式中那些是一元一次不等式 ( )
⑴、 ⑶
*
二、交流对话,巩固练习
例1 下列各式中,哪些是一元一次不等式
-y≤3 ② 3x-y>0 ③ 0.5x-3<1
3>1 ⑤ 3x=5 ⑥
⑦ ⑧
√
√
√
注:在实际判断中主要看它是不是符
合一元一次不等式的四个关键词
*
二、交流对话,巩固练习
1、
2、若a>b,则下列不等式中不正确的是( )
A a-5 >b-5 B -5a >-5b
C a+8 >b+8 D
3、
≤
<
B
x≤2
*
4、不等式 的解是_______。
5、已知不等式的解表示在数轴上如图所示,则对应的不等式是( )
A x+2>1 B x-1≤0 C 2x+2≥0 D x+1≤0
C
二、交流对话,巩固练习
*
6、
7、若不等式(b-1)x<b-1的解是x>1,则b的
取值范围是______.
x=1
b<1
二、交流对话,巩固练习
*
8、 ( )
A 2(x+2)-(1-2x) >1 B 2(x+2)-1-2x >4
C 2(x+2)-(1-2x) >4 D 2x+2-(1-2x) >4
C
二、交流对话,巩固练习
*
二、交流对话,巩固练习
9、
A B
C D
( )
D
*
例2、解不等式 ,并将
解集表示在数轴上
总结:
(1)去分母时,不等式中不含分母的项不要漏乘公
分母
(2)去分母后,不等式中分子是多项式的要加括号
(3)最后一步将系数化为1时,注意要变向
*
解下列不等式,并把解在数轴上表示出来:
*
三、变式拓展,感悟提升
1、若关于x的不等式-3(x-2) >3a+x的解
是x<3,求a的值。
总结: 本类型的题目有多种形式,常常是方程中蕴含着不等式,或者是不等式与不等式的解(数轴)之间相互联系。事实上,在出题时往往是多个知识点结合在一起出现。解题时一定要注意理清相互之间的关系,学会具体问题具体分析,灵活运用数形结合,待定系数法等数学思想。
2、若关于x的方程3(x+2)=2a+x的解是
一个负数,且a是一个正整数,求这
个方程的解。
*
3、已知函数y=-2x+4的自变量的取值范围是x<1,求函数值y的取值范围。
三、变式拓展,感悟提升
*
四、聪明题
1、若不等式3x-m≤0的正整数解是1,2,3
试求m的取值范围.
2、
9≤m<12
3或1
4、由不等式(m-5)x> m-5变形为x< 1,则m需满足的条件是 ,
3、若a >b,且a、b为有理数,则am2 bm2
6、若不等式组 无解,
则a的取值范围是 ;
x> a+2
x<3a-2
2、若y= -x+7,且2≤y≤7,则x的取值范围是 ,
5、已知不等式3x-m ≤0有4个正整数解,则m的取值范围是 ,
0≤x≤5
≥
m<5
12≤m< 15
a≤ 2
A
B
C
6
8
7、在⊿ABC中,AB=8,AC=6,则BC的
取值范围__________
21A
B
C
D
8、在上述条件下,若AD是BC边上的中线,
则AD的取值范围________
8
6
6
E
9、若 是关于x的一元
一次不等式则 a 的值( )
-2
例1、解下列不等式(组)并在数轴上表示出来。
(1) -
-5
解:去分母得:4(2x-1)-2(10x+1)
15x-60
移项,合并同类项 得:-27x
-54
x
2
在数轴上表示如图所示:
1
2
0
(1)解不等式 ,并把解在数轴上表示出来。
(2)不等式 的非负整数解是 。
0、1
(3)x取什么值时,代数式 的值不大于 的值?
并求x的最大值。
1、解一元一次不等式,并把解在数轴上表示出来:
2、求使不等式3(x-3)-1<2x成立的正整数解。
练一练
3、解不等式
并把它的解集表示的数轴上。
其解集在数轴上表示如右图
练一练
4、解不等式
并把它的解集在数轴上表示出来。
解集在数轴上表示如右图
同大取大
的解集是
当a>b时,
X>a
X>b
X>a
同小取小
的解集是
当a>b时,
X<a
X<b
X<b
大小小大取中间
的解集是
当a>b时,
X<a
X≥b
b ≤ X<a
大小等同取等值
X=a
的解集是
X≥a
X≤a
不等式组
大大小小则无解
的解集是
当a>b时,
X > a
X < b
无解
文字记忆
数学语言
图形
一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
a
b
解:由(1)得:2x+6>X+5 则 x>-1
由(2)得x-2
0则x
2
-12
用数轴表示:
2
0
-1
例3、解不等式组
2(x+3)>x+5 (1)
0 (2)
(1)解一元一次不等式组 2x+3≥4 ①
3x-2≤2x+3 ②
(2)不等式组4≤3x-2≤2x+3的所有整数解的和是 。
(3)如果4,3m-2,2m+3这三个数在数轴上所对应的点
从左到右依次排列,则m的取值范围是 。
(4)不等式组 2x+3≥m 的解是 x≥5,则的取值范围
3x-2≥2x+3
是 。
14
2<m<5
m≤13
试一试
1、关于 的不等式 的解集如图所示,
则a的值是 。
-2 -1 0 1 2
1
2、已知不等式3x-m ≤0有1、2两个正整数解,则m的取值范围是 。
6≤m<9
解这个不等式,得
∴y的正整数解是:1,2,3,4。
例5、y取何正整数时,代数式2(y-1)的值不大于10-4(y-3)的值。
解:根据题意列出不等式:
解:解方程组得:
x=-m+7
y=2m-5
因为它的解是正数,所以:
-m+7>0
2m-5>0
所以
2.5例6、 求使方程组:
x+y=m+2
4x+5y=6m+3
的解x ,y都是正数的m的取值范围
1、如果关于x的方程3(x+2)=2a+x的根是个负数,且a是一个正整数,试确定x的值。
练一练
∴
根据题意,得
解得 m>2
的解大于1。
2、m取何值时,关于x的方程
做一做:
填空:
1.若x=3-2a且1/5(x-3)2已知|2x-4|+(3x-y-m)2=0且y<0 则m的范围是( )
3已知不等式4x-a a的正整数解是1, 2,则a的取值范围是( )
4若不等式2x+k<5-x没有正数解则k的范围是( )
5同时满足-3x 0与4x+7>0的整数是( )
6不等式(a-1)x1 则a的范围是( )
a<1.5
m>6
4 a<6
K 2
0 ,-1
a<1
7、不等式组
6x-1>3x-4
-1/3 x 2/3
的整数解为( )
9、如果mA、m-9-n C、1/n >1/m D、m/n >1
10、已知关于x的方程 =-1的解是非负数,则a
的范围不正确的是( )
A、 a 2 B、a 2
C、a<2且a -4 D、a 2且a -4
0 ,1
a 3
A B D
A B C
8、若不等式组
X>3
X>a
的解集是x>a则a的范围是( )
1、解关于x的不等式: k(x+3)>x+4;
解:去括号,得kx+3k>x+4;
移项得kx-x > 4 -3k ; 得(k-1)x > 4 -3k ;
若k-1=0, 即k=1时,0>1不成立,
∴不等式无解。
若k-1>0,即k>1时,
若k-1<0,即k<1时,
。
是同解不等式?如果存在,求出整数m和不等式
的解集;如果不存在,请说明理由。
与
2、是否存在整数m,使关于x的不等式
x>-8
3、已知不等式3x-a≤0的正整数解是1,2,3,求a的范围
变式1:不等式3x-a<0的正整数解为1,2,3,求a的范围
变式2:不等式3x-a>0的负整数解为-1,-2,求a的范围
变式3:不等式3x-a≥0的负整数解为-1,-2,求a的范围
4、不等式组 无解,求a的范围
{
x>2a-1
x<3
{
x≥2a-1
x<3
不等式组
无解,求a的范围
变式一:
{
x≥2a-1
x ≤ 3
不等式组
无解,求a的范围
变式二:
5、已知,不等式组 3(x-4)< 2(4x+5)-2
>
①求此不等式组的整数解
②若上述整数解满足方程ax-3=3a-x,求a的值
③ 在① ②的条件下,求代数式 的值
例、王海贷款5万元去做生意,贷款月利息10‰ .他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱?(精确到100元)
月利息=本金×利率
本息=本金+利息
解:设王海平均每月要赚x元钱。根据题意得
6x≥50000+50000×10‰×6
解得
答:王海平均每个月至少要赚8900元钱。
根据题意得取x=8900
例、某网吧有两种收费形式:1、计时制:3元/小时;2、包月制:60元/月,另加1元/小时,请问在什么情况下采用计时制合算,在什么情况下采用包月制合算?
做一做:
1、一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小答对了x道题,则得4x分,另有(25-x)道要扣分,而小明评为优秀,即小明的得分应大于或等于85分,
4x-(25-x) ≥85
解得: x≥22
所以,小明到少答对了22道题,他可能答对22,23,24或25道题。
y1=200×0.75x,即y1=150x,
y2=200×0.8(x-1),即y2=160x-160,
y1= y2时,150x=160x-160, 解得x=16;
y1 >y2时,150x>160x-160, 解得x<16;
y1< y2时,150x<160x-160, 解得x>16;
2、某单位计划在新年期间组织员工到某地旅游,参如旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一定旅行社支付的旅游费用较少?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1,选择乙旅行社时,所需的费用为y2,则:
所以,当人数为16人时,甲、乙两家旅行社的收费相同;当人数为17~25人时,选择甲旅行社费用较少;当人数为10~15人时,选择乙旅行社费用较少。
3、某商品的零售价是每件50元,进价是每件35元。经核算,每天商店的各种费用(包括房租、售货员工资等)是120元,还需把商品售出价的10%上缴税款,问商店每天需要出售多少件这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
解:设商店每天出售该商品x件。根据题意得
(50-35-50×10%)x-120>100
解得
答:商店每天需要出售23件或23件以上这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
即 10x>220
x>22
4、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
*
不等式的性质
1、不等式的传递性
2、不等式的两边都加上(或减去)
同一个数,所得不等式仍成立
3、不等式的两边都乘(或都除以)
同一个正数,所得不等式仍成立
不等式的两边都都乘(或都除以)
同一个负数,必须把不等号改变方向,所得不等式仍成立
一元一次
不等式
解一元一次不等式
解一元一次不等式组
在数轴上表示
不等式的解
*
用不等式表示不相等的数量关系(即列不等式)时,要正确理解其中的关键词语,恰当选用不等号。这种关键词语大致上可以分为以下几种情况,请在空格里填上适当的不等号。
关键
词语
第一类
(明确表明数量的不等关系)
第二类
(明确表明数量的范围特征)
大于、
比..大
小于、
比..小
不大于
不超过
至多
不小于
不低于
至少
正数
负数
非正数
非负数
不等号
0
0
0
0
>
<
≤
≥
>
<
≤
≥
根据下列数量关系列不等式:
⑴、a不是正数。
⑵、x与y的一半的差大于-3。
⑶、y的70%与5的和是非负数。
⑷、3与x的倒数的差小于5。
⑸、a的立方根不等于a。
上述不等式中那些是一元一次不等式 ( )
⑴、 ⑶
*
二、交流对话,巩固练习
例1 下列各式中,哪些是一元一次不等式
-y≤3 ② 3x-y>0 ③ 0.5x-3<1
3>1 ⑤ 3x=5 ⑥
⑦ ⑧
√
√
√
注:在实际判断中主要看它是不是符
合一元一次不等式的四个关键词
*
二、交流对话,巩固练习
1、
2、若a>b,则下列不等式中不正确的是( )
A a-5 >b-5 B -5a >-5b
C a+8 >b+8 D
3、
≤
<
B
x≤2
*
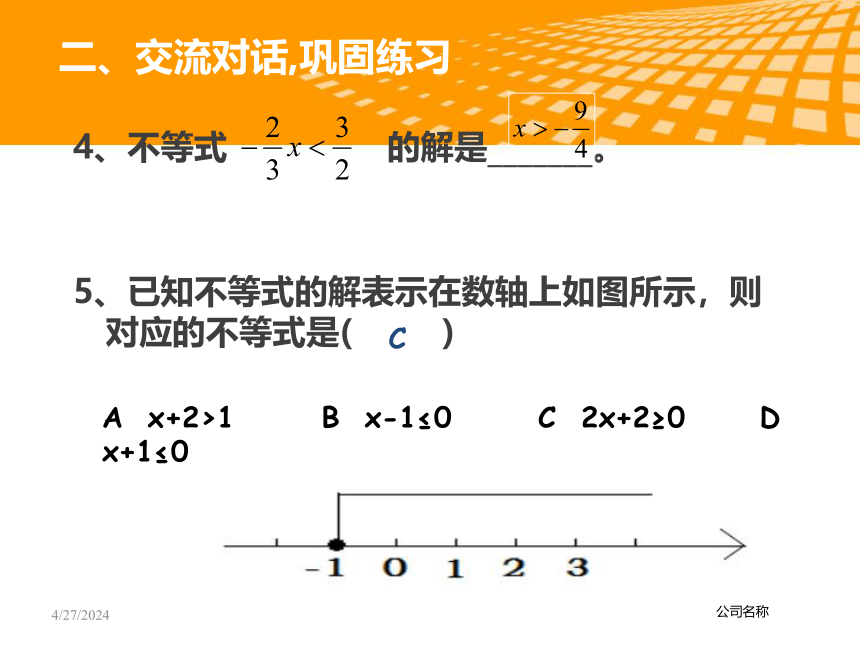
4、不等式 的解是_______。
5、已知不等式的解表示在数轴上如图所示,则对应的不等式是( )
A x+2>1 B x-1≤0 C 2x+2≥0 D x+1≤0
C
二、交流对话,巩固练习
*
6、
7、若不等式(b-1)x<b-1的解是x>1,则b的
取值范围是______.
x=1
b<1
二、交流对话,巩固练习
*
8、 ( )
A 2(x+2)-(1-2x) >1 B 2(x+2)-1-2x >4
C 2(x+2)-(1-2x) >4 D 2x+2-(1-2x) >4
C
二、交流对话,巩固练习
*
二、交流对话,巩固练习
9、
A B
C D
( )
D
*
例2、解不等式 ,并将
解集表示在数轴上
总结:
(1)去分母时,不等式中不含分母的项不要漏乘公
分母
(2)去分母后,不等式中分子是多项式的要加括号
(3)最后一步将系数化为1时,注意要变向
*
解下列不等式,并把解在数轴上表示出来:
*
三、变式拓展,感悟提升
1、若关于x的不等式-3(x-2) >3a+x的解
是x<3,求a的值。
总结: 本类型的题目有多种形式,常常是方程中蕴含着不等式,或者是不等式与不等式的解(数轴)之间相互联系。事实上,在出题时往往是多个知识点结合在一起出现。解题时一定要注意理清相互之间的关系,学会具体问题具体分析,灵活运用数形结合,待定系数法等数学思想。
2、若关于x的方程3(x+2)=2a+x的解是
一个负数,且a是一个正整数,求这
个方程的解。
*
3、已知函数y=-2x+4的自变量的取值范围是x<1,求函数值y的取值范围。
三、变式拓展,感悟提升
*
四、聪明题
1、若不等式3x-m≤0的正整数解是1,2,3
试求m的取值范围.
2、
9≤m<12
3或1
4、由不等式(m-5)x> m-5变形为x< 1,则m需满足的条件是 ,
3、若a >b,且a、b为有理数,则am2 bm2
6、若不等式组 无解,
则a的取值范围是 ;
x> a+2
x<3a-2
2、若y= -x+7,且2≤y≤7,则x的取值范围是 ,
5、已知不等式3x-m ≤0有4个正整数解,则m的取值范围是 ,
0≤x≤5
≥
m<5
12≤m< 15
a≤ 2
A
B
C
6
8
7、在⊿ABC中,AB=8,AC=6,则BC的
取值范围__________
2
B
C
D
8、在上述条件下,若AD是BC边上的中线,
则AD的取值范围________
8
6
6
E
9、若 是关于x的一元
一次不等式则 a 的值( )
-2
例1、解下列不等式(组)并在数轴上表示出来。
(1) -
-5
解:去分母得:4(2x-1)-2(10x+1)
15x-60
移项,合并同类项 得:-27x
-54
x
2
在数轴上表示如图所示:
1
2
0
(1)解不等式 ,并把解在数轴上表示出来。
(2)不等式 的非负整数解是 。
0、1
(3)x取什么值时,代数式 的值不大于 的值?
并求x的最大值。
1、解一元一次不等式,并把解在数轴上表示出来:
2、求使不等式3(x-3)-1<2x成立的正整数解。
练一练
3、解不等式
并把它的解集表示的数轴上。
其解集在数轴上表示如右图
练一练
4、解不等式
并把它的解集在数轴上表示出来。
解集在数轴上表示如右图
同大取大
的解集是
当a>b时,
X>a
X>b
X>a
同小取小
的解集是
当a>b时,
X<a
X<b
X<b
大小小大取中间
的解集是
当a>b时,
X<a
X≥b
b ≤ X<a
大小等同取等值
X=a
的解集是
X≥a
X≤a
不等式组
大大小小则无解
的解集是
当a>b时,
X > a
X < b
无解
文字记忆
数学语言
图形
一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
a
b
解:由(1)得:2x+6>X+5 则 x>-1
由(2)得x-2
0则x
2
-1
用数轴表示:
2
0
-1
例3、解不等式组
2(x+3)>x+5 (1)
0 (2)
(1)解一元一次不等式组 2x+3≥4 ①
3x-2≤2x+3 ②
(2)不等式组4≤3x-2≤2x+3的所有整数解的和是 。
(3)如果4,3m-2,2m+3这三个数在数轴上所对应的点
从左到右依次排列,则m的取值范围是 。
(4)不等式组 2x+3≥m 的解是 x≥5,则的取值范围
3x-2≥2x+3
是 。
14
2<m<5
m≤13
试一试
1、关于 的不等式 的解集如图所示,
则a的值是 。
-2 -1 0 1 2
1
2、已知不等式3x-m ≤0有1、2两个正整数解,则m的取值范围是 。
6≤m<9
解这个不等式,得
∴y的正整数解是:1,2,3,4。
例5、y取何正整数时,代数式2(y-1)的值不大于10-4(y-3)的值。
解:根据题意列出不等式:
解:解方程组得:
x=-m+7
y=2m-5
因为它的解是正数,所以:
-m+7>0
2m-5>0
所以
2.5
x+y=m+2
4x+5y=6m+3
的解x ,y都是正数的m的取值范围
1、如果关于x的方程3(x+2)=2a+x的根是个负数,且a是一个正整数,试确定x的值。
练一练
∴
根据题意,得
解得 m>2
的解大于1。
2、m取何值时,关于x的方程
做一做:
填空:
1.若x=3-2a且1/5(x-3)
3已知不等式4x-a a的正整数解是1, 2,则a的取值范围是( )
4若不等式2x+k<5-x没有正数解则k的范围是( )
5同时满足-3x 0与4x+7>0的整数是( )
6不等式(a-1)x
a<1.5
m>6
4 a<6
K 2
0 ,-1
a<1
7、不等式组
6x-1>3x-4
-1/3 x 2/3
的整数解为( )
9、如果m
10、已知关于x的方程 =-1的解是非负数,则a
的范围不正确的是( )
A、 a 2 B、a 2
C、a<2且a -4 D、a 2且a -4
0 ,1
a 3
A B D
A B C
8、若不等式组
X>3
X>a
的解集是x>a则a的范围是( )
1、解关于x的不等式: k(x+3)>x+4;
解:去括号,得kx+3k>x+4;
移项得kx-x > 4 -3k ; 得(k-1)x > 4 -3k ;
若k-1=0, 即k=1时,0>1不成立,
∴不等式无解。
若k-1>0,即k>1时,
若k-1<0,即k<1时,
。
是同解不等式?如果存在,求出整数m和不等式
的解集;如果不存在,请说明理由。
与
2、是否存在整数m,使关于x的不等式
x>-8
3、已知不等式3x-a≤0的正整数解是1,2,3,求a的范围
变式1:不等式3x-a<0的正整数解为1,2,3,求a的范围
变式2:不等式3x-a>0的负整数解为-1,-2,求a的范围
变式3:不等式3x-a≥0的负整数解为-1,-2,求a的范围
4、不等式组 无解,求a的范围
{
x>2a-1
x<3
{
x≥2a-1
x<3
不等式组
无解,求a的范围
变式一:
{
x≥2a-1
x ≤ 3
不等式组
无解,求a的范围
变式二:
5、已知,不等式组 3(x-4)< 2(4x+5)-2
>
①求此不等式组的整数解
②若上述整数解满足方程ax-3=3a-x,求a的值
③ 在① ②的条件下,求代数式 的值
例、王海贷款5万元去做生意,贷款月利息10‰ .他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱?(精确到100元)
月利息=本金×利率
本息=本金+利息
解:设王海平均每月要赚x元钱。根据题意得
6x≥50000+50000×10‰×6
解得
答:王海平均每个月至少要赚8900元钱。
根据题意得取x=8900
例、某网吧有两种收费形式:1、计时制:3元/小时;2、包月制:60元/月,另加1元/小时,请问在什么情况下采用计时制合算,在什么情况下采用包月制合算?
做一做:
1、一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小答对了x道题,则得4x分,另有(25-x)道要扣分,而小明评为优秀,即小明的得分应大于或等于85分,
4x-(25-x) ≥85
解得: x≥22
所以,小明到少答对了22道题,他可能答对22,23,24或25道题。
y1=200×0.75x,即y1=150x,
y2=200×0.8(x-1),即y2=160x-160,
y1= y2时,150x=160x-160, 解得x=16;
y1 >y2时,150x>160x-160, 解得x<16;
y1< y2时,150x<160x-160, 解得x>16;
2、某单位计划在新年期间组织员工到某地旅游,参如旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一定旅行社支付的旅游费用较少?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1,选择乙旅行社时,所需的费用为y2,则:
所以,当人数为16人时,甲、乙两家旅行社的收费相同;当人数为17~25人时,选择甲旅行社费用较少;当人数为10~15人时,选择乙旅行社费用较少。
3、某商品的零售价是每件50元,进价是每件35元。经核算,每天商店的各种费用(包括房租、售货员工资等)是120元,还需把商品售出价的10%上缴税款,问商店每天需要出售多少件这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
解:设商店每天出售该商品x件。根据题意得
(50-35-50×10%)x-120>100
解得
答:商店每天需要出售23件或23件以上这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
即 10x>220
x>22
4、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
*
