华东师大版 数学七年级下册第七章 一次方程组 复习 课件(共16张PPT)
文档属性
| 名称 | 华东师大版 数学七年级下册第七章 一次方程组 复习 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 318.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览






文档简介
第七章 一次方程组
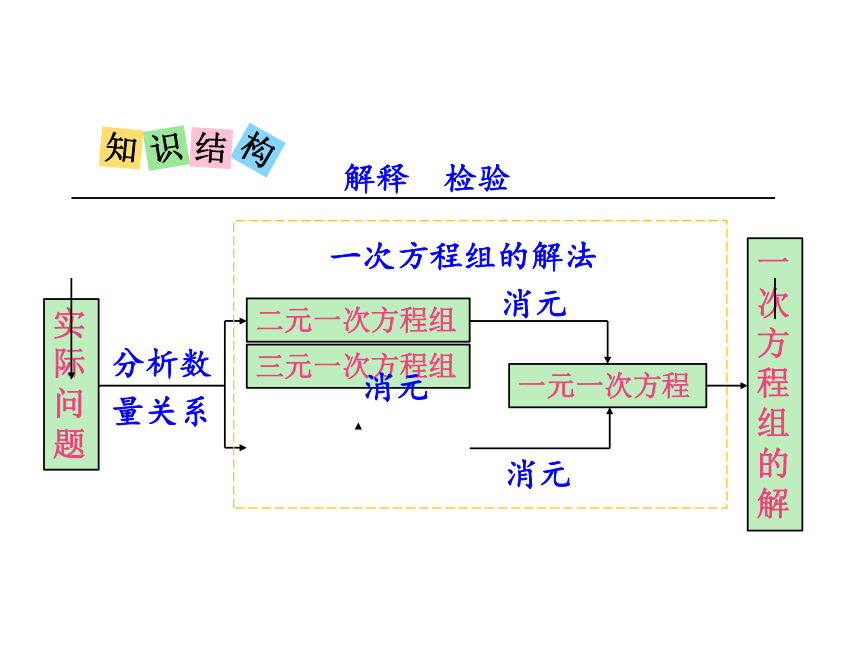
识
构
结
知
实际问题
一次方程组的解
二元一次方程组
三元一次方程组
一元一次方程
分析数量关系
消元
消元
消元
一次方程组的解法
解释 检验
识
点
要
知
含有两个未知数,每个未知数的项的次数都是 1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.组成二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
什么是二元一次方程组?什么是二元一次方程组的解?
问题
1
解二元一次方程组的基本思路是消元.
解二元一次方程组的基本思路是什么?
问题
2
联系:都是消元,转化为一元一次方程,最后求出方程组的解。
区别:未知数和方程的个数不同。
解三元一次方程组与解二元一次方程组有什么联系和区别?
问题
3
(1)审题;(2)设未知数;(3)列出方程组;(4)解方程组;(5)检验;(6)作答.
用二元一次方程组解决实际问题的基本步骤是什么?
问题
4
随堂演练
1.下列 x,y 的值是方程组 的解的是( )
A
2.解下列方程组最适合用代入法的是( )
A
(1) (2)
3. 解下列方程
解:(1) ①×3 得 x + 3y = 3,即 x = 3 – 3y.
原方程组的解为
代入②得 5(3 – 3y)– 4y = – 4,即 y = 1.
(1)
①②
代入①得 x = 0.
(2)
①②
解:(1) ②×3 + ①得 8y = 16,即 y = 2.
原方程组的解为
代入②得 10 – 2x = – 8,即 x = 9.
4. 1 号仓库与 2 号仓库共存粮 450 t,现从 1 号仓库运出存粮的 60%,从 2 号仓库运出存粮的 40%,结果 2 号仓库所余粮食比 1 号仓库所余粮食多 30 t,1 号仓库与 2 号仓库原来各存粮多少吨?
解:设 1 号仓库原来存粮 x t,2 号仓库原来存粮 y t.
由题意,得
解得
答:设 1 号仓库原来存粮 240 t,2 号仓库原来存粮 210 t.
解:设 1 角、5 角、1 元的硬币分别取 x 枚、y 枚、z 枚,
5. 现有 1 角、5 角、1 元硬币各 10 枚,从中取出 15 枚,共值 7 元. 1 角、5 角、1 元硬币各取多少枚?
由题意,得
①②
② – ①,得 4y + 9z = 55,
∵x,y,z 都小于等于 10,且只能取正整数,
答:应取 5 枚 1 角,7 枚 5 角和 3 枚 1 元的硬币.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
识
构
结
知
实际问题
一次方程组的解
二元一次方程组
三元一次方程组
一元一次方程
分析数量关系
消元
消元
消元
一次方程组的解法
解释 检验
识
点
要
知
含有两个未知数,每个未知数的项的次数都是 1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.组成二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
什么是二元一次方程组?什么是二元一次方程组的解?
问题
1
解二元一次方程组的基本思路是消元.
解二元一次方程组的基本思路是什么?
问题
2
联系:都是消元,转化为一元一次方程,最后求出方程组的解。
区别:未知数和方程的个数不同。
解三元一次方程组与解二元一次方程组有什么联系和区别?
问题
3
(1)审题;(2)设未知数;(3)列出方程组;(4)解方程组;(5)检验;(6)作答.
用二元一次方程组解决实际问题的基本步骤是什么?
问题
4
随堂演练
1.下列 x,y 的值是方程组 的解的是( )
A
2.解下列方程组最适合用代入法的是( )
A
(1) (2)
3. 解下列方程
解:(1) ①×3 得 x + 3y = 3,即 x = 3 – 3y.
原方程组的解为
代入②得 5(3 – 3y)– 4y = – 4,即 y = 1.
(1)
①②
代入①得 x = 0.
(2)
①②
解:(1) ②×3 + ①得 8y = 16,即 y = 2.
原方程组的解为
代入②得 10 – 2x = – 8,即 x = 9.
4. 1 号仓库与 2 号仓库共存粮 450 t,现从 1 号仓库运出存粮的 60%,从 2 号仓库运出存粮的 40%,结果 2 号仓库所余粮食比 1 号仓库所余粮食多 30 t,1 号仓库与 2 号仓库原来各存粮多少吨?
解:设 1 号仓库原来存粮 x t,2 号仓库原来存粮 y t.
由题意,得
解得
答:设 1 号仓库原来存粮 240 t,2 号仓库原来存粮 210 t.
解:设 1 角、5 角、1 元的硬币分别取 x 枚、y 枚、z 枚,
5. 现有 1 角、5 角、1 元硬币各 10 枚,从中取出 15 枚,共值 7 元. 1 角、5 角、1 元硬币各取多少枚?
由题意,得
①②
② – ①,得 4y + 9z = 55,
∵x,y,z 都小于等于 10,且只能取正整数,
答:应取 5 枚 1 角,7 枚 5 角和 3 枚 1 元的硬币.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
